Which of the following is/are not SHM?
y=Acosωt
y=Asinωt
y=Asin3ωt
y=AekT
The correct Answer is:D
To determine which of the given options is not Simple Harmonic Motion (SHM), we need to analyze the equations provided and check if they satisfy the condition for SHM. The condition for SHM is given by the equation:
d2xdt2=−ω2x
This means that the acceleration of the object is directly proportional to its displacement from the equilibrium position and is always directed towards that position.
Step 1: Analyze the first option
Let's consider the first option, which is x=Acos(ωt).
1. Differentiate x with respect to time t:
dxdt=−Aωsin(ωt)
2. Differentiate again to find acceleration:
d2xdt2=−Aω2cos(ωt)
3. Substitute x=Acos(ωt) into the SHM equation:
d2xdt2=−ω2x
This shows that this option satisfies the SHM condition.
Step 2: Analyze the second option
Now, let's consider the second option, which is x=Asin(ωt).
1. Differentiate x with respect to time t:
dxdt=Aωcos(ωt)
2. Differentiate again to find acceleration:
d2xdt2=−Aω2sin(ωt)
3. Substitute x=Asin(ωt) into the SHM equation:
d2xdt2=−ω2x
This option also satisfies the SHM condition.
Step 3: Analyze the third option
Next, consider the third option, which is x=Aekt.
1. Differentiate x with respect to time t:
dxdt=Akekt
2. Differentiate again to find acceleration:
d2xdt2=Ak2ekt
3. Substitute x=Aekt into the SHM equation:
d2xdt2=−ω2x
This gives:
Ak2ekt=−ω2Aekt
If we cancel Aekt (assuming A≠0), we get:
k2=−ω2
This is not possible since both k2 and ω2 are positive quantities. Therefore, this option does not satisfy the SHM condition.
Conclusion
Thus, the option that is not SHM is:
D) x=Aekt
Let's consider the first option, which is x=Acos(ωt).
dxdt=−Aωsin(ωt)
d2xdt2=−Aω2cos(ωt)
d2xdt2=−ω2x
Now, let's consider the second option, which is x=Asin(ωt).
dxdt=Aωcos(ωt)
d2xdt2=−Aω2sin(ωt)
d2xdt2=−ω2x
Next, consider the third option, which is x=Aekt.
dxdt=Akekt
d2xdt2=Ak2ekt
d2xdt2=−ω2x
Ak2ekt=−ω2Aekt
k2=−ω2
Thus, the option that is not SHM is:
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Assignment (Section - A) (OBJECTIVE TYPE QUESTIONS)
60 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Assignment (Section - B) (OBJECTIVE TYPE QUESTIONS)
30 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - EXAMPLE
21 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
4 Videos
Similar Questions
Which of the following represents a SHM?
View SolutionWhich of the following is correct about a SHM, along a straight line?
View SolutionWhich of the following is a necessary and sufficient condition for S.H.M.
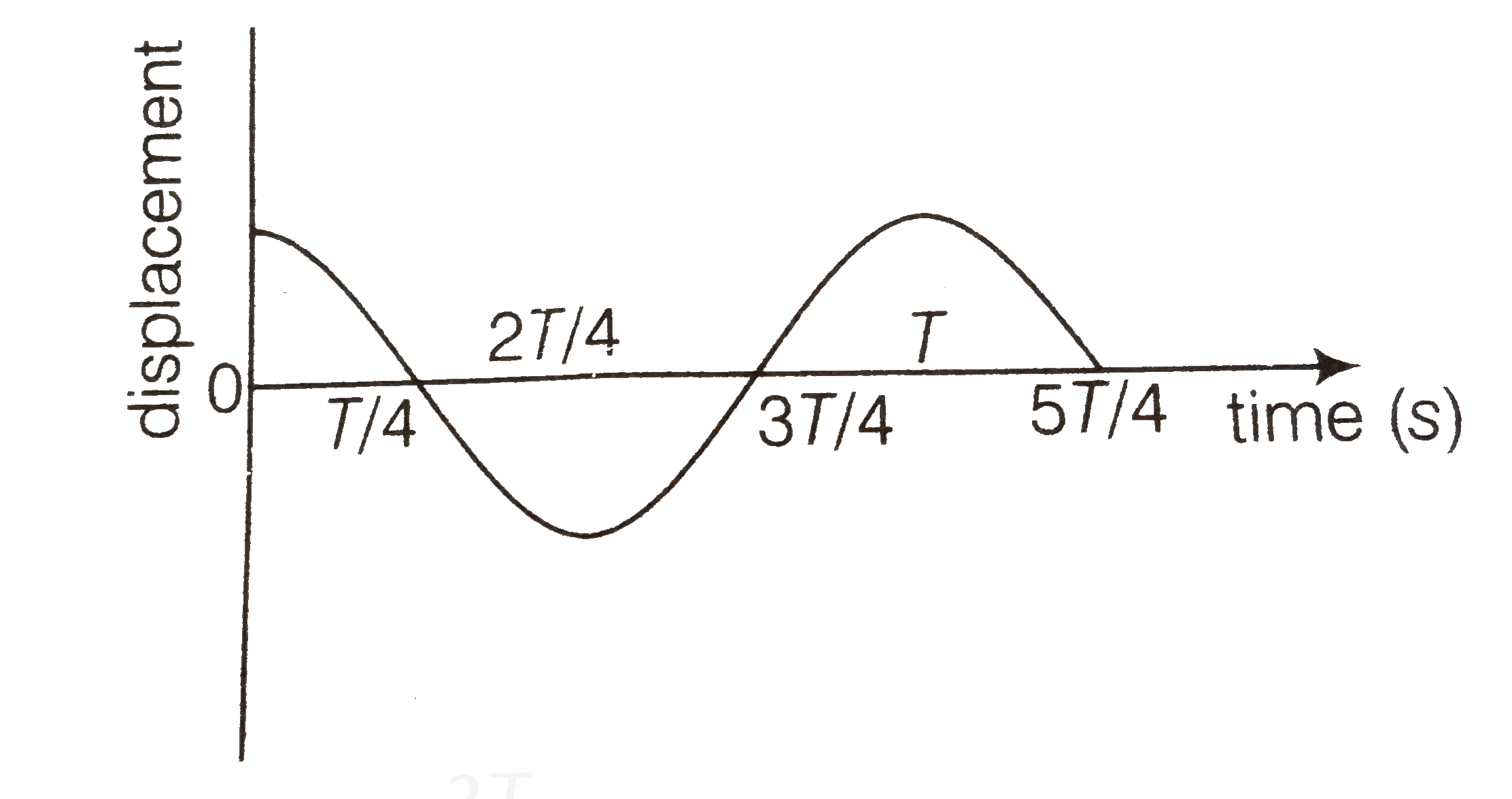
View SolutionThe displacement-time graph of a particle executing SHM is shown in figure. Which of the following statement is/are true ?
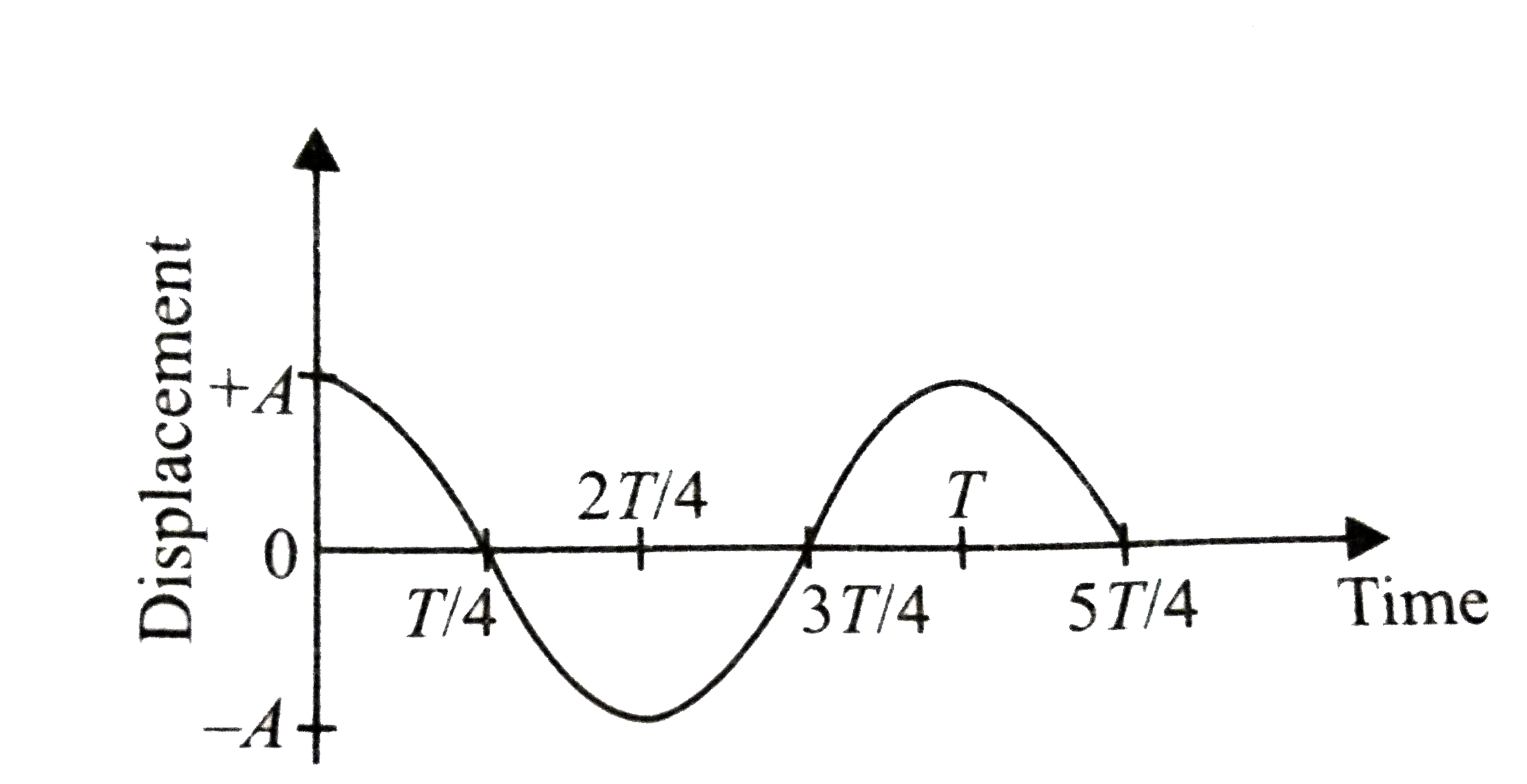
View SolutionThe displacement-time graph for a particle executing SHM is as shown in figure. Which of the following statements is correct?
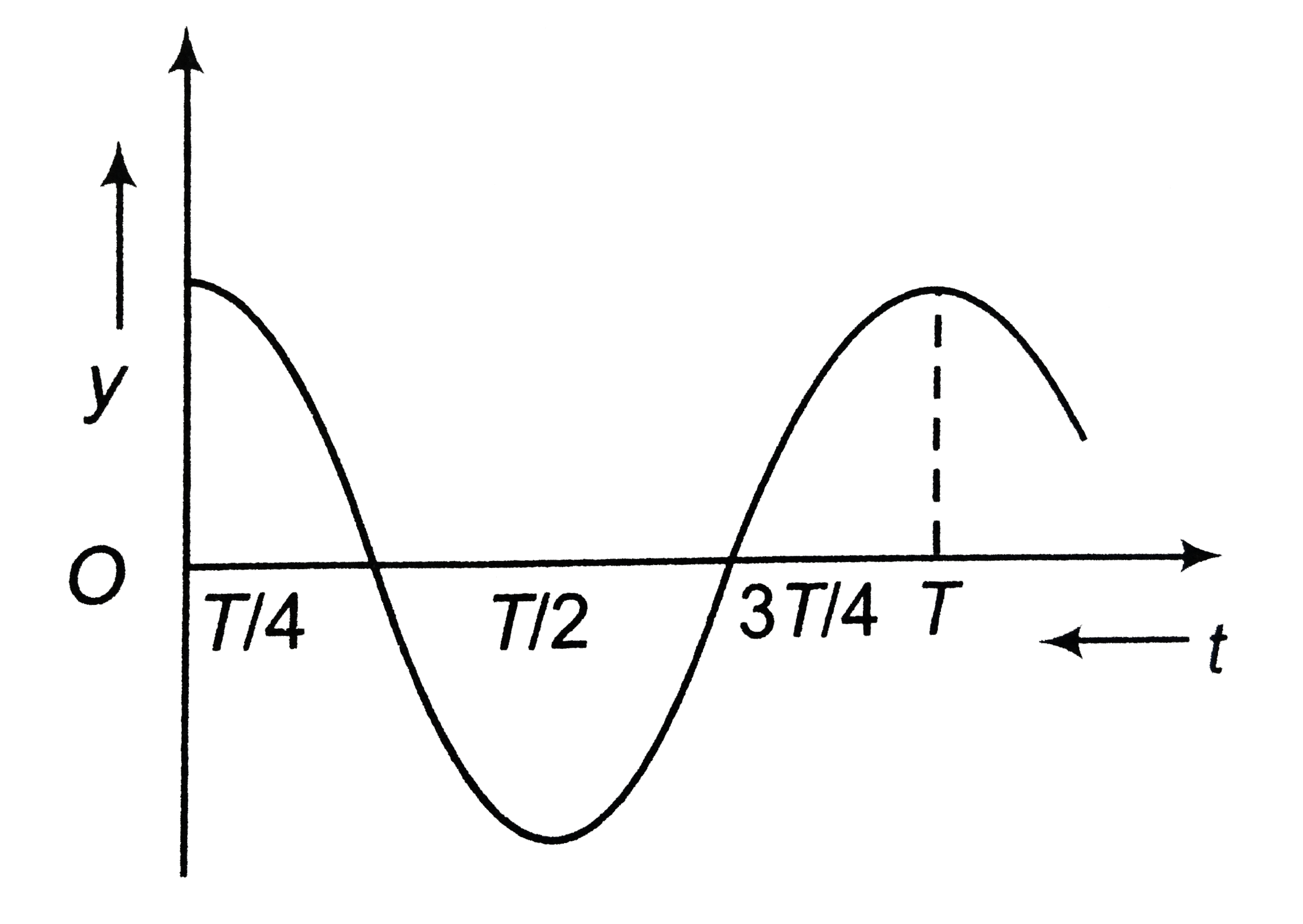
View SolutionThe displacement - time graph of a particle executing SHM is shown in figure. Which of the following statements is//are true ?
View SolutionThe displacement time graph of a particle executing S.H.M. (in straight line) is shown. Which of the following statements is true?
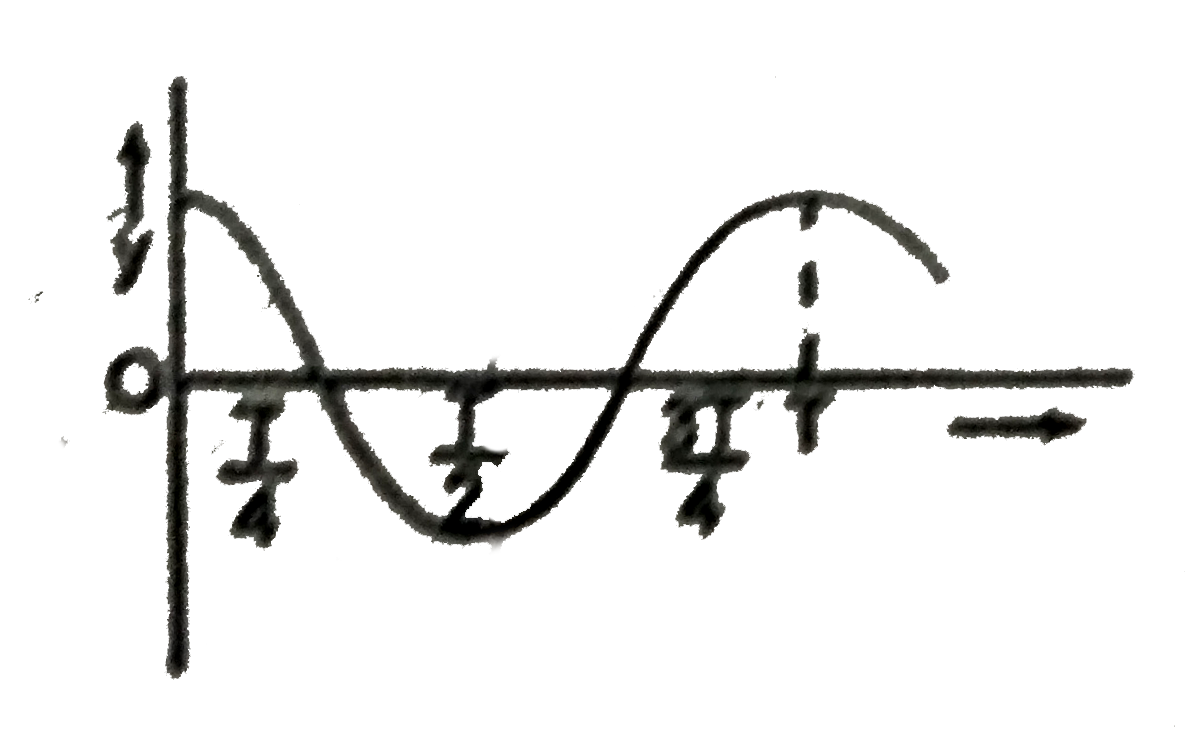
View SolutionThe displecement-time graph of a particle execting SHM is shown in figure. Which of the following statements is false?
View SolutionThe graph in the figure shows how the displacement of a particle describing S.H.M. varies with time. Which one of the following statements is not true ?

View SolutionFor a particle executing S.H.M. which of the following statements holds good :
View Solution
