For the damped oscillator shown in previous figure, k=180Nm−1 and the damping constant b is 40gs−1 .Period of oscillation is given as 0.3 s, find the mass of the block . (Assume b is much less than √km).
Hint :T=2π√mk
T=2π√mk
m=T2k4π2
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION -A)
58 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT (SECTION-B )
25 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Assignment (Section D) (ASSERTION-REASON TYPE QUESTIONS)
13 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
4 Videos
Similar Questions
For the damped oscillator shown in Fig, the mass of the block is 200g,k=80Nm−1 and the damping constant b is 40gs−1 Calculate
The period of oscillation

View SolutionFor the small damping oscillator, the mass of the block is 500 g and value of spring constant is k = 50 N/m and damping constant is 10gs^(-1) The time period of oscillation is (approx.)
View Solution
Knowledge Check
A block of mass 200 g executing SHM under the influence of a spring of spring constant k=90Nm−1 and a damping constant b=40gs−1. The time elapsed for its amplitude to drop to half of its initial value is (Given, ln (1/2)=−0.693)
A7sB9sC4sD11s
For the damped oscillator shown in Figure, the mass m of the block is 400 g, k=45Nm−1 and the damping constant b is 80gs−1. Calculate .
(a) The period of osciallation ,
(b) Time taken for its amplitude of vibrations to drop to half of its initial value and
(c ) The time taken for its mechanical energy to drop to half its initial value.
View SolutionA 5kg collar is attached to a spring . It slides without friction over a horizontal surface. It is displaced from its equilibrium position by 10 cm and released , its maximum speed is 1ms−1 Calculate
(a) Spring constant
(b) The period of oscillation
(c ) Maximum acceleration of the collar
Hint :m=5kg,A=0.1m,k=?,T=?or a=?,vm=1ms−1
vm=Aω=A√km
Find k,
T=2π√mk
amax=ω2A=kmA
View Solution
For a damped oscillator which follow the equation →F=−k→x−b→V
the mass of the block is 100 gm K=100N/M and the damping constant is 20 gm/sec. thhen find the time taken for its mechanical energy to drop to one-fourth of its initial value.
View SolutionThe angular frequency of the damped oscillator is given by ω=√km−r24m2 ,where k is the spring constant, m is the mass of the oscillator and r is the damping constant. If the ratio r2/(mk) is 8% ,the change in the time period compared to the undamped oscillator
View SolutionAs shown in the figure, two light springs of force constant k1 and k2 oscillate a block of mass m. Its effective force constant will be

View SolutionBlock of mass m2 is in equilibrium as shown in figure. Anotherblock of mass m1 is kept gently on m2. Find the time period of oscillation and amplitude.
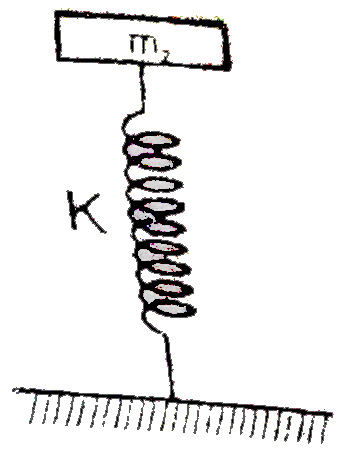
View SolutionBlock of mass m2 is in equilibrium as shown in figure. Anotherblock of mass m1 is kept gently on m2. Find the time period of oscillation and amplitude.
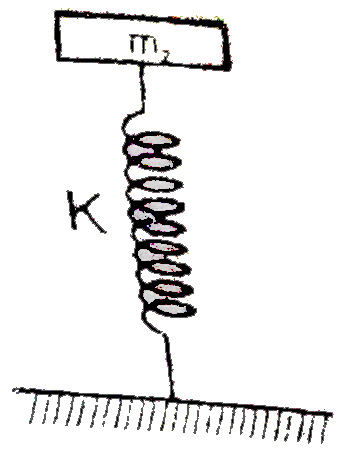
View Solution
