A simple pendulum of mass m executes SHM with total energy E. if at an instant it is at one of extreme positions, then its linear momentum after a phase shift of π3 rad will be
√2mE
√3mE2
2√mE
√2mE3
The correct Answer is:B
To solve the problem step by step, we will follow the reasoning and calculations outlined in the video transcript.
Step 1: Understand the Energy of the Simple Harmonic Motion (SHM)
The total energy E of a simple pendulum executing SHM is given by the formula:
E=12mω2A2
where:
- m is the mass of the pendulum,
- ω is the angular frequency,
- A is the amplitude of the motion.
Step 2: Determine the Displacement at Phase Shift
At one of the extreme positions, the displacement x is equal to the amplitude A. When the phase shifts by π3 radians, we can express the new displacement as:
x=Acos(π3)
Calculating cos(π3):
cos(π3)=12
Thus, the displacement becomes:
x=A⋅12=A2
Step 3: Calculate the Velocity
The velocity v of the pendulum can be calculated using the formula:
v=ω√A2−x2
Substituting x=A2:
v=ω√A2−(A2)2
Calculating (A2)2:
(A2)2=A24
Thus, we have:
v=ω√A2−A24=ω√3A24=ω⋅√32A
Step 4: Calculate the Linear Momentum
The linear momentum p is given by:
p=m⋅v
Substituting the expression for v:
p=m⋅(√32Aω)=√32mAω
Step 5: Relate Aω to Total Energy
From the energy equation, we know:
E=12mω2A2
We can express Aω in terms of E:
Aω=√2Em
Substituting this back into the momentum equation:
p=√32m⋅√2Em=√32√2Em
Final Step: Simplify the Expression
Thus, the final expression for the linear momentum is:
p=√3E
Conclusion
The linear momentum after a phase shift of π3 radians is:
p=√3E
The total energy E of a simple pendulum executing SHM is given by the formula:
E=12mω2A2
where:
- m is the mass of the pendulum,
- ω is the angular frequency,
- A is the amplitude of the motion.
At one of the extreme positions, the displacement x is equal to the amplitude A. When the phase shifts by π3 radians, we can express the new displacement as:
x=Acos(π3)
Calculating cos(π3):
cos(π3)=12
Thus, the displacement becomes:
x=A⋅12=A2
The velocity v of the pendulum can be calculated using the formula:
v=ω√A2−x2
Substituting x=A2:
v=ω√A2−(A2)2
Calculating (A2)2:
(A2)2=A24
Thus, we have:
v=ω√A2−A24=ω√3A24=ω⋅√32A
The linear momentum p is given by:
p=m⋅v
Substituting the expression for v:
p=m⋅(√32Aω)=√32mAω
From the energy equation, we know:
E=12mω2A2
We can express Aω in terms of E:
Aω=√2Em
Substituting this back into the momentum equation:
p=√32m⋅√2Em=√32√2Em
Thus, the final expression for the linear momentum is:
p=√3E
The linear momentum after a phase shift of π3 radians is:
p=√3E
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Assignment (Section C) (PREVIOUS YEARS QUESTIONS)
43 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Assignment (Section D) (ASSERTION-REASON TYPE QUESTIONS)
13 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Assignment (Section - A) (OBJECTIVE TYPE QUESTIONS)
60 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
4 Videos
Similar Questions
A simple pendulum of mass m and length L is held in horizontal position. If it is released from this position, then find the angular momentum of the bob about the point of suspension when it is vertically below the point of suspension.
View SolutionA particle of mass 0.10 kg executes SHM with an amplitude 0.05 m and frequency 20 vib/s. Its energy of oscillation is
View Solution
Knowledge Check
A simple pendulum executing SHM with a period of 6 s between two extreme positions B and C about a point O. if the length of the arc BC is 10 cm, how long will the pendulum take the move from position C to a position D towards O exactly midway between C and O?
A0.5 sB1 sC1.5 sD3 sConsider the following statements regarding particle executing simple harmonic motion :
(1) The total energy of the particle constant
(2) The restoring force is minimum at the extreme positions
(3) the velocity of the particle is minimum at the mean position
Which of the these statements are correct ?A1 and 2B1 and 4C2 and 3D3 and 4A particle of mass m is subjected to an attractive central force of magnitude k/r2, k being a constant. If at the instant when the particle is at an extreme position in its closed orbit, at a distance a from the centre of force, its speed is √k/2ma, if the distance of other extreme position is b. Find a/b.
A2B3C4D5
A body executes SHM with an amplitude a. At what displacement from the mean positions, the potentail energy of the body is one-fourth of its total energy?
View SolutionA particle of mass m executes SHM with amplitude 'a' and frequency 'v'. The average kinetic energy during motion from the position of equilibrium to the end is:
View SolutionThe figure below shows a simple pendulum of mass 200 g. It is displaced from the mean position A to the extreme position B. The potential energy at the position A is zero. At the position B the pendulum bob is raised by 5 m.
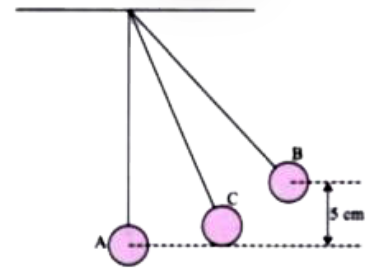
(i) What is the potential energy of the pendulum at the position B?
(ii) What is the total mechanical energy at point C?
(iii) What is the speed of the bob at the position A when released from B ?
(Take g = 10ms−2 and there is no loss of energy.)
View SolutionA horizontal spring mass system is executing SHM with time period of 4s. At time t=0, it is at mean position. Find the minimum time after which its potential energy becomes three times of kinetic energy.
View SolutionA paticle of mass m is executing uniform circular motion on a path of radius r. If p is the magnitude of its linear momentum, then the radial force acting on the particle is
View Solution