A simple pendulum of mass m and length L is held in horizontal position. If it is released from this position, then find the angular momentum of the bob about the point of suspension when it is vertically below the point of suspension.
mL√2gL
mL√gL
mL√3gL
none
The correct Answer is:A
To find the angular momentum of the bob about the point of suspension when it is vertically below the point of suspension, we can follow these steps:
Step 1: Understand the Initial and Final States
Initially, the pendulum is held horizontally at a height L above the lowest point. When released, it swings down to the lowest point, where the height is zero.
Step 2: Apply Conservation of Mechanical Energy
The mechanical energy conservation principle states that the total mechanical energy (potential + kinetic) remains constant if only conservative forces are acting.
- Initial Potential Energy (PE_initial) at height L:
PEinitial=mgh=mgL
- Initial Kinetic Energy (KE_initial):
KEinitial=0(since it is released from rest)
- Final Potential Energy (PE_final) at the lowest point:
PEfinal=0
- Final Kinetic Energy (KE_final) when the bob is at the lowest point:
KEfinal=12mv2
Using conservation of energy:
PEinitial+KEinitial=PEfinal+KEfinal
Substituting the values:
mgL+0=0+12mv2
Step 3: Solve for Velocity v
Rearranging the equation:
mgL=12mv2
Cancelling m from both sides (assuming m≠0):
gL=12v2
Multiplying both sides by 2:
2gL=v2
Taking the square root:
v=√2gL
Step 4: Calculate Angular Momentum
The angular momentum L about the point of suspension is given by:
L=r⋅p
where r is the distance from the pivot (length of the pendulum L) and p is the linear momentum p=mv.
Thus,
L=L⋅mv=mL⋅√2gL
Step 5: Final Expression for Angular Momentum
So, the angular momentum L about the point of suspension is:
L=mL√2gL
Summary
The angular momentum of the bob about the point of suspension when it is vertically below the point of suspension is:
L=mL√2gL
Initially, the pendulum is held horizontally at a height L above the lowest point. When released, it swings down to the lowest point, where the height is zero.
The mechanical energy conservation principle states that the total mechanical energy (potential + kinetic) remains constant if only conservative forces are acting.
PEinitial=mgh=mgL
- Initial Kinetic Energy (KE_initial):
KEinitial=0(since it is released from rest)
PEfinal=0
KEfinal=12mv2
PEinitial+KEinitial=PEfinal+KEfinal
Substituting the values:
mgL+0=0+12mv2
Rearranging the equation:
mgL=12mv2
Cancelling m from both sides (assuming m≠0):
gL=12v2
Multiplying both sides by 2:
2gL=v2
Taking the square root:
v=√2gL
The angular momentum L about the point of suspension is given by:
L=r⋅p
where r is the distance from the pivot (length of the pendulum L) and p is the linear momentum p=mv.
L=L⋅mv=mL⋅√2gL
So, the angular momentum L about the point of suspension is:
L=mL√2gL
The angular momentum of the bob about the point of suspension when it is vertically below the point of suspension is:
L=mL√2gL
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (GRAVITATION)25videos
RACE
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Properties of Matter & Fluid Mechanics)(Elasticity)20videos
RACE
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (COLLISION AND CENTRE OF MASS )12videos
RACE
- BOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III28videos
NEWTONS LAWS OF MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example1videos
SIMPLE HARMONIC MOTION
Similar Questions
A rigid rod of mass m & length l is pivoted at one of its ends. If it is released from its horizontal position, find the speed of the centre of mass of the rod when it becomes vertical.
View SolutionA rod of mass m and length L is pivoted at a point O and kept in horizontal position as shown in figure. Now it is released from this position so that it can rotates freely about the point O in downward direction. When it becomes vertical
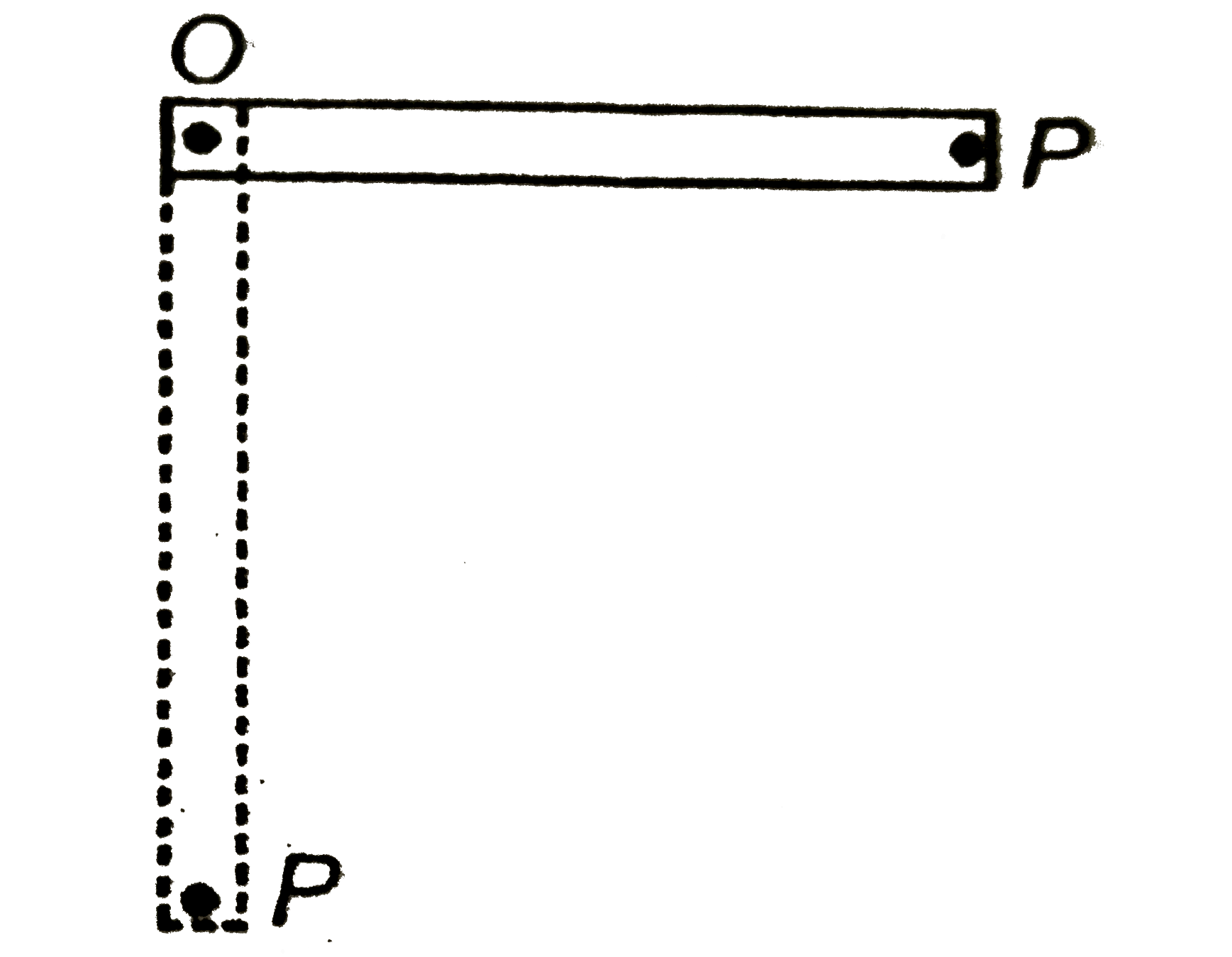 View Solution
View SolutionA simple pendulum of length l is pulled aside to make an angle θ with the vertical. Find the magnitude of the torque of the weight w of the bob about the point of suspension. When is the torque zero?
View SolutionA simple pendilum with bob of mass m and length l is held in position at an angle θ with t he verticle. Find its speed when it passes the lowest position.
View SolutionA body of mass m is projected with a velocity u at an angle θ with the horizontal. The angular momentum of the body, about the point of projection, when it at highest point on its trajectory is
View SolutionA simple pendulum of length l and mass m is initially at its lowest position. It is given the minimum horizontal speed necessary after to move in a circular path about the point of suspension. The tension in the string at the lowest positive of the bob is
View SolutionA simple pendulum is released from rest with the string in horizontal position. The vertical component of the velocity of the bob becomes maximum, when the string makes an angle θ with the vertical. The angle θ is equal to
View SolutionIf a particle of mass m is thrown with speed at an angle 60° with horizontal, then angular momentum of particle at highest point about point of projection is
View SolutionA uniform disc of mass m and radius R is pivoted at point P and is free rotate in vertical plane. The centre C of disc is initially in horizontal position with P as shown in figure. If it is released from this position, then its angular acceleration when the line PC is inclined to the horizontal at an angle θ is
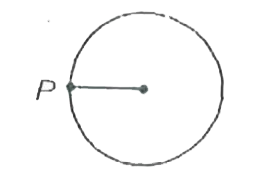 View Solution
View SolutionA simple pendulum with bob of mass m and length x is held in position at an angle θ1 and then angle θ2 with the vertical. When released from these positions, speeds with which it passes the lowest postions are v1&v2 respectively. Then ,v1v2 is.
View Solution

