Two charges of +25×10−9 coulomb and −25×10−9 coulomb are placed 6 m apart. Find the electric field intensity ratio at points 4 m from the centre of the electric dipole (i) on axial line (ii) on equatorial line
100049
491000
50049
49500
The correct Answer is:A
To find the electric field intensity ratio at points 4 m from the center of the electric dipole (i) on the axial line and (ii) on the equatorial line, we can follow these steps:
Step 1: Understand the Configuration
We have two charges:
- q1=+25×10−9 C (positive charge)
- q2=−25×10−9 C (negative charge)
The distance between the two charges is 6 m. The center of the dipole is at the midpoint between the two charges, which is 3 m from each charge.
Step 2: Define the Points of Interest
- Axial Line: A point P is located 4 m from the center of the dipole along the axial line.
- Equatorial Line: A point Q is also located 4 m from the center but on the equatorial line.
Step 3: Calculate Electric Field Intensity on the Axial Line
The formula for the electric field intensity Ea on the axial line of a dipole is given by:
Ea=2kpr2−a2
where:
- k is Coulomb's constant (9×109N m2/C2)
- p is the dipole moment, given by p=q⋅d (where d is the distance between the charges)
- r is the distance from the center to the point of interest (4 m)
- a is half the distance between the charges (3 m)
Calculating the dipole moment p:
p=q⋅d=(25×10−9)⋅6=150×10−9C m
Now substituting values into the axial electric field formula:
Ea=2⋅(9×109)⋅(150×10−9)42−32
Calculating the denominator:
42−32=16−9=7
Thus,
Ea=2⋅(9×109)⋅(150×10−9)7
Step 4: Calculate Electric Field Intensity on the Equatorial Line
The formula for the electric field intensity Ee on the equatorial line of a dipole is given by:
Ee=kpr2+a2
Substituting the same values:
Ee=(9×109)⋅(150×10−9)42+32
Calculating the denominator:
42+32=16+9=25
Thus,
Ee=(9×109)⋅(150×10−9)25
Step 5: Calculate the Ratio of Electric Fields
Now, we find the ratio EaEe:
EaEe=2⋅(9×109)⋅(150×10−9)7(9×109)⋅(150×10−9)25
The (9×109) and (150×10−9) cancel out:
EaEe=2⋅257=507
Final Result
Thus, the electric field intensity ratio at the two points is:
EaEe=100049
We have two charges:
- q1=+25×10−9 C (positive charge)
- q2=−25×10−9 C (negative charge)
- Axial Line: A point P is located 4 m from the center of the dipole along the axial line.
- Equatorial Line: A point Q is also located 4 m from the center but on the equatorial line.
The formula for the electric field intensity Ea on the axial line of a dipole is given by:
Ea=2kpr2−a2
where:
- k is Coulomb's constant (9×109N m2/C2)
- p is the dipole moment, given by p=q⋅d (where d is the distance between the charges)
- r is the distance from the center to the point of interest (4 m)
- a is half the distance between the charges (3 m)
p=q⋅d=(25×10−9)⋅6=150×10−9C m
Ea=2⋅(9×109)⋅(150×10−9)42−32
Calculating the denominator:
42−32=16−9=7
Thus,
Ea=2⋅(9×109)⋅(150×10−9)7
The formula for the electric field intensity Ee on the equatorial line of a dipole is given by:
Ee=kpr2+a2
Substituting the same values:
Ee=(9×109)⋅(150×10−9)42+32
Calculating the denominator:
42+32=16+9=25
Thus,
Ee=(9×109)⋅(150×10−9)25
Now, we find the ratio EaEe:
EaEe=2⋅(9×109)⋅(150×10−9)7(9×109)⋅(150×10−9)25
The (9×109) and (150×10−9) cancel out:
EaEe=2⋅257=507
Thus, the electric field intensity ratio at the two points is:
EaEe=100049
Similar Questions
Two charges +20μCand−20μC are held 1cm apart. Calculate the electric field at a point on the equatorial line at a distance of 50cm from the center of the dipole.
View SolutionTwo charges +20μC and −20μC are 5 mm apart. Find the electric field on axial as well as on the equatorial line at a distance 20 cm from the mid -point of the dipole.
View SolutionTwo charges +20μCand−20μC are placed 10mm apart. The electric field at point P, on the axis of the dipole 10 cm away from its centre O on the side of the positive charge is
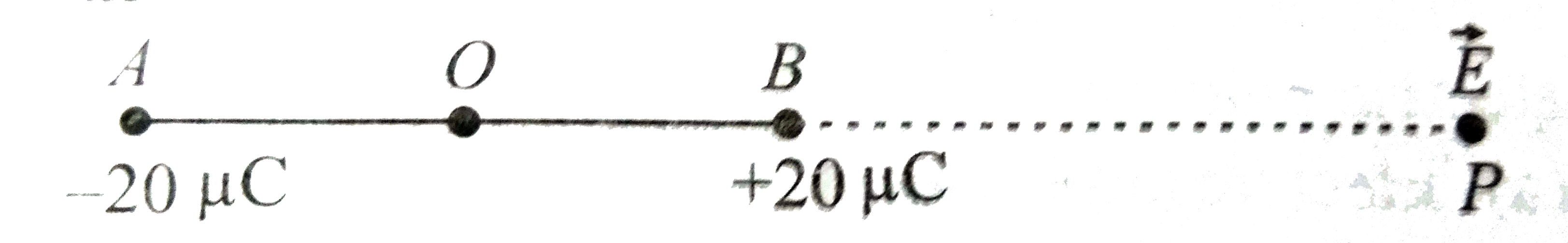
View SolutionTwo charges, each of 5μC but opposite in sign, are placed 4 cm apart. Calculate the electric field intensity of a point that is a distance 4 cm from the mid point on the axial line of the dipole.
View SolutionTwo point charges +5×10−19Cand+20×10−19C are separated by a distance of 2m. The electric field intensity will be zero at a distance d=………. From the charges of 5×1019C.
View SolutionTwo charges 10μC are placed 5.0 mm apart. Determine the electric field at a point P on the axis of the dipole 15 cm away from its centre O on the side of the positive charge, as shown in Fig.
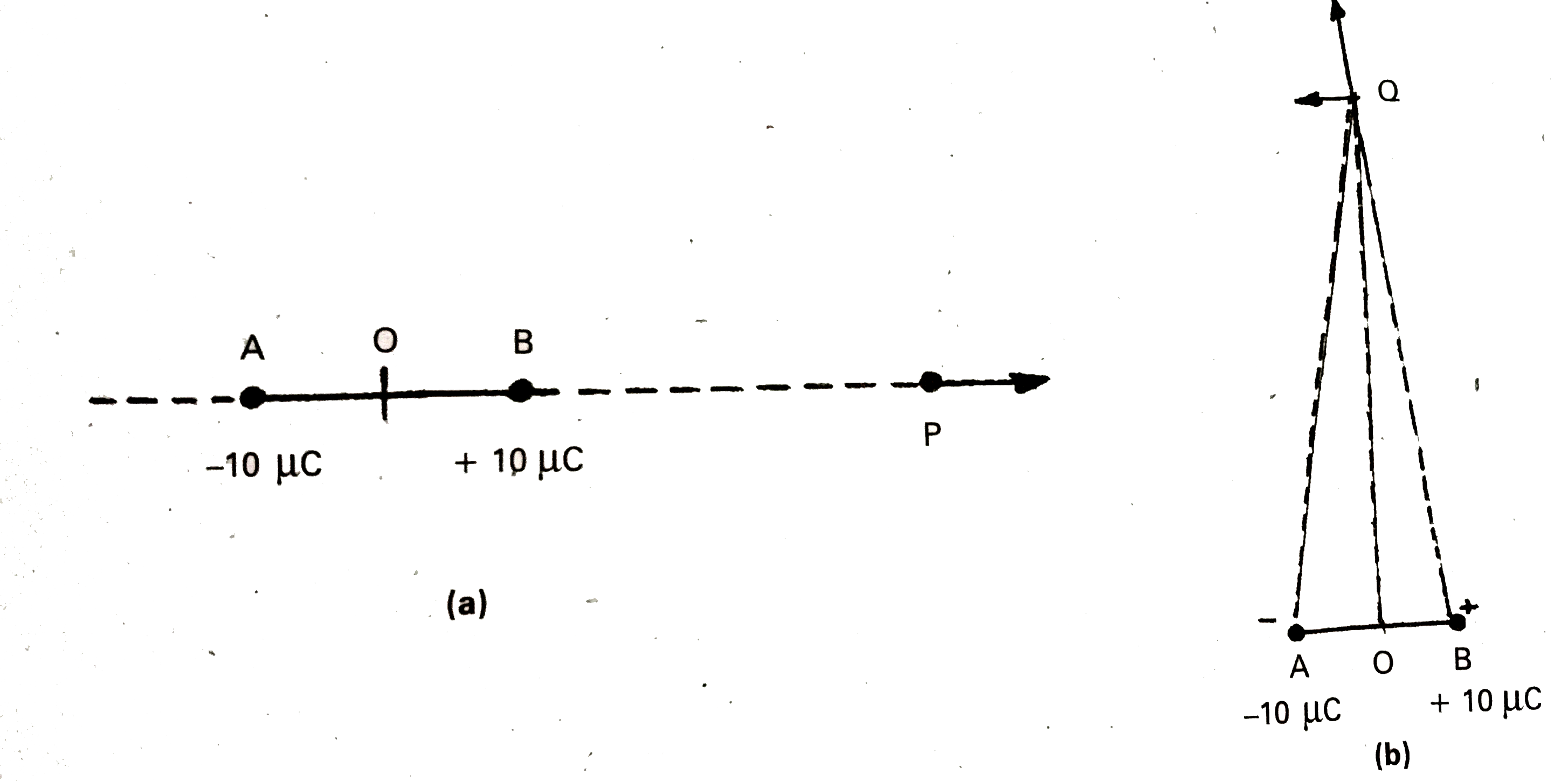
View SolutionTwo charges +5μC and +10μC are placed 20cm apart. The net electric field at the mid-point between the two charges is
View SolutionTwo like charges of magnitude 1×10−9 coulomb and 9×10−9 coulomb are separated by a distance of 1 meter. The point on the line joining the charges , where the force experienced by a charge placed at that point is zero , is
View SolutionTwo charges 2 nano coulombs and -6 nano coulombs are separated by 16 cm in air. The resultant electric intensity at the zero potential point which lies in between them and on the line joining them is
View SolutionA point charge of 5×10−6C experiences a force of 2×10−3N when kept in a uniform electric field of intensity E. Find E.
View Solution
