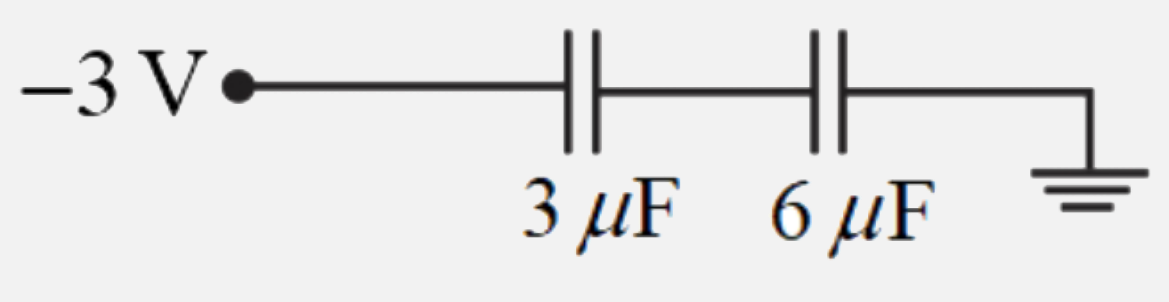Compare the expression for magnetic energy density with electrostatic energy density stored in the space between the plates of a parallel plate capacitor.
The electrostatic energy stored
U=12(q22ε0A)×d ...(i)
( where C is the capacitance, C=ε0Ad) q is the charge upon capacitor)
Now the electric field in the space (between plates of capacitor)
E=qε0A ...(ii)
From equation (i) and (ii)
U=12(qε0A)2×ε0×A×d
⇒U=12ε0E2×volume
Hence UVolume=12ε0)E2 (iii)
This expression can be compared with magnetic energy per unit volume which is equal to B22μ0 (iv)
Similar Questions
Knowledge Check
As the distance between the plates of a parallel plate capacitor decreased
AIf both assertion and reason are ture and reason is the correct explanation of assertion.BIf both assertin and reason are ture but reason is not the correct explanation of assertion .CIf assertion is true but reason is false.DIf both assertion and reason are false.
(b) Obtain the expression for the capacitance of a parallel plate capacitor.
View SolutionDerive the expression for the magnetic energy stored in a solenoid in terms of magnetic field B, area A and length l of the solenoid carrying a steady current 1. How does this magnetic energy per unit volume compare with the electrostatic energy density stored in a parallel plate capacitor ?
View SolutionDeduce an expression for the potential energy stored in a parallel plate capacitor.
View SolutionThe expression for the capacity of the capacitor formed by compound dielectric placed between the plates of a parallel plate capacitor as shown in figure, will be (area of plate =A)

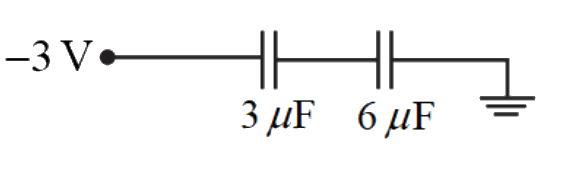
View SolutionThe total electrostatic energy stored in both the capacitors (in μJ) is
View SolutionIf the separation between the plates of a capacitor is 5 mm , then area of the plate of a 3 F parallel plate capacitor is
View SolutionUsing the concept of energy density, find the total energy stored in a
a. parallel plate capacitor
b. charged spherical conductor.
View Solution