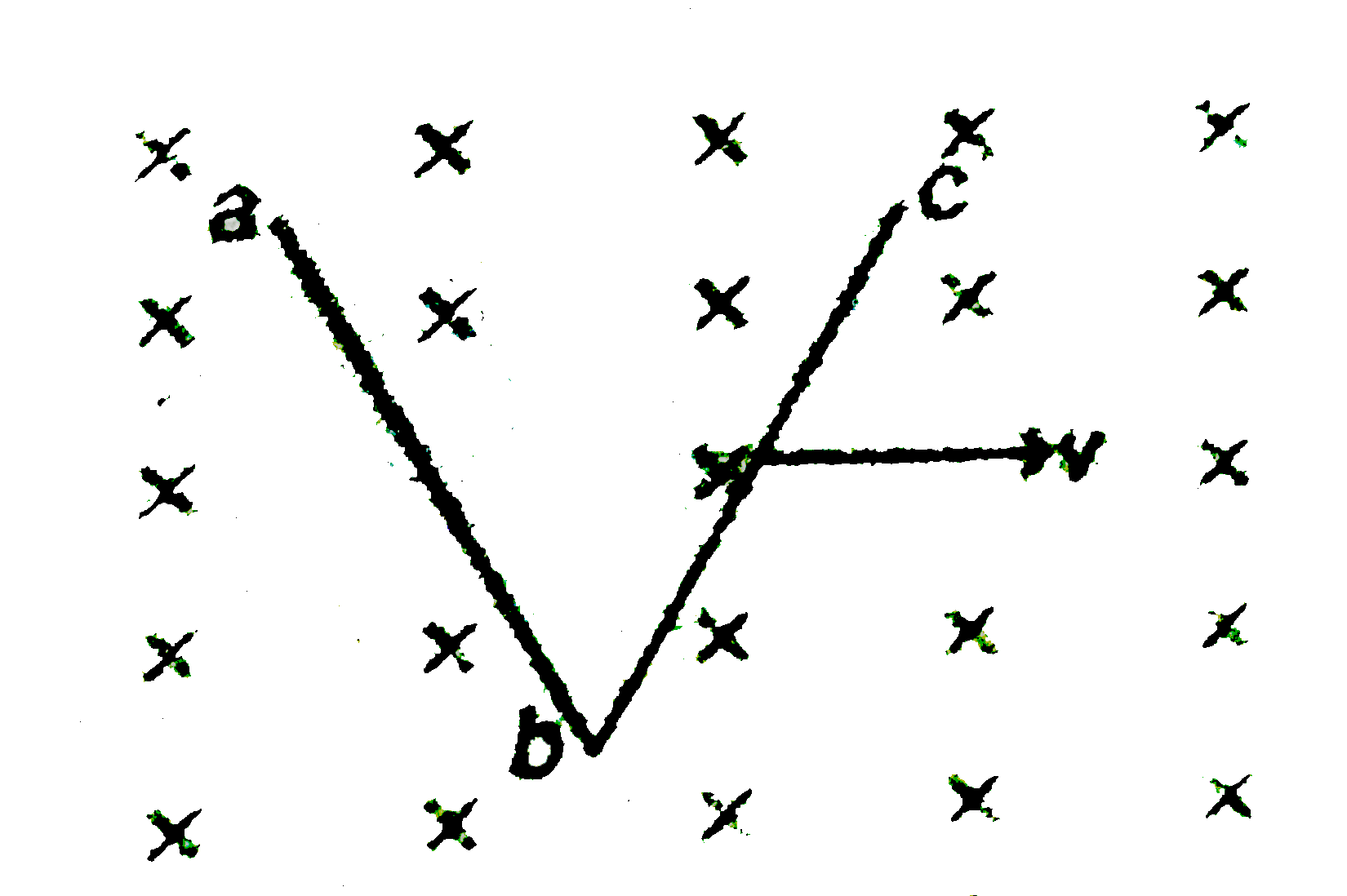
A rod AB slides on a V shaped wire with speed v as shown, such that at any time OA = OB = I. Magnetic field in the region is perpendicular downwards and has strength B, induced emf in the rod is
Zero
Bvl
√3Bvl2
Bvl2
The correct Answer is:B
To find the induced electromotive force (emf) in the rod AB that slides on a V-shaped wire, we can follow these steps:
1. Understanding the Setup:
- We have a rod AB that is sliding on a V-shaped wire. The rod moves with a speed v.
- The lengths OA and OB are equal and denoted as L.
- The magnetic field B is directed downwards, perpendicular to the plane of the wire.
2. Identifying the Geometry:
- The angle of the V-shaped wire is 60∘.
- The rod AB can be considered as part of an isosceles triangle where OA = OB = L.
3. Using the Formula for Induced EMF:
- The induced emf (E) in a conductor moving through a magnetic field can be calculated using the formula:
E=∫(v⋅B)dl
- Here, v is the velocity of the rod, B is the magnetic field strength, and dl is the differential length element along the rod.
4. Simplifying the Expression:
- Since the rod is moving with a constant speed v and the magnetic field B is uniform, we can simplify the integral:
E=B⋅v⋅L
- Here, L is the effective length of the conductor in the magnetic field.
5. Conclusion:
- The induced emf in the rod AB is given by:
E=BvL
Final Answer:
The induced emf in the rod is E=BvL.
---
- We have a rod AB that is sliding on a V-shaped wire. The rod moves with a speed v.
- The lengths OA and OB are equal and denoted as L.
- The magnetic field B is directed downwards, perpendicular to the plane of the wire.
- The angle of the V-shaped wire is 60∘.
- The rod AB can be considered as part of an isosceles triangle where OA = OB = L.
- The induced emf (E) in a conductor moving through a magnetic field can be calculated using the formula:
E=∫(v⋅B)dl
- Here, v is the velocity of the rod, B is the magnetic field strength, and dl is the differential length element along the rod.
- Since the rod is moving with a constant speed v and the magnetic field B is uniform, we can simplify the integral:
E=B⋅v⋅L
- Here, L is the effective length of the conductor in the magnetic field.
- The induced emf in the rod AB is given by:
E=BvL
The induced emf in the rod is E=BvL.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION - A) (OBJECTIVE TYPE QUESTIONS)
35 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION - B) (OBJECTIVE TYPE QUESTIONS)
25 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - J)
5 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - comprehension
3 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
Similar Questions
A V-shaped conducting wire is moved inside a magnetic field as shown in figure. Magnetic fiel d is perpendicular to paper inwards. Then
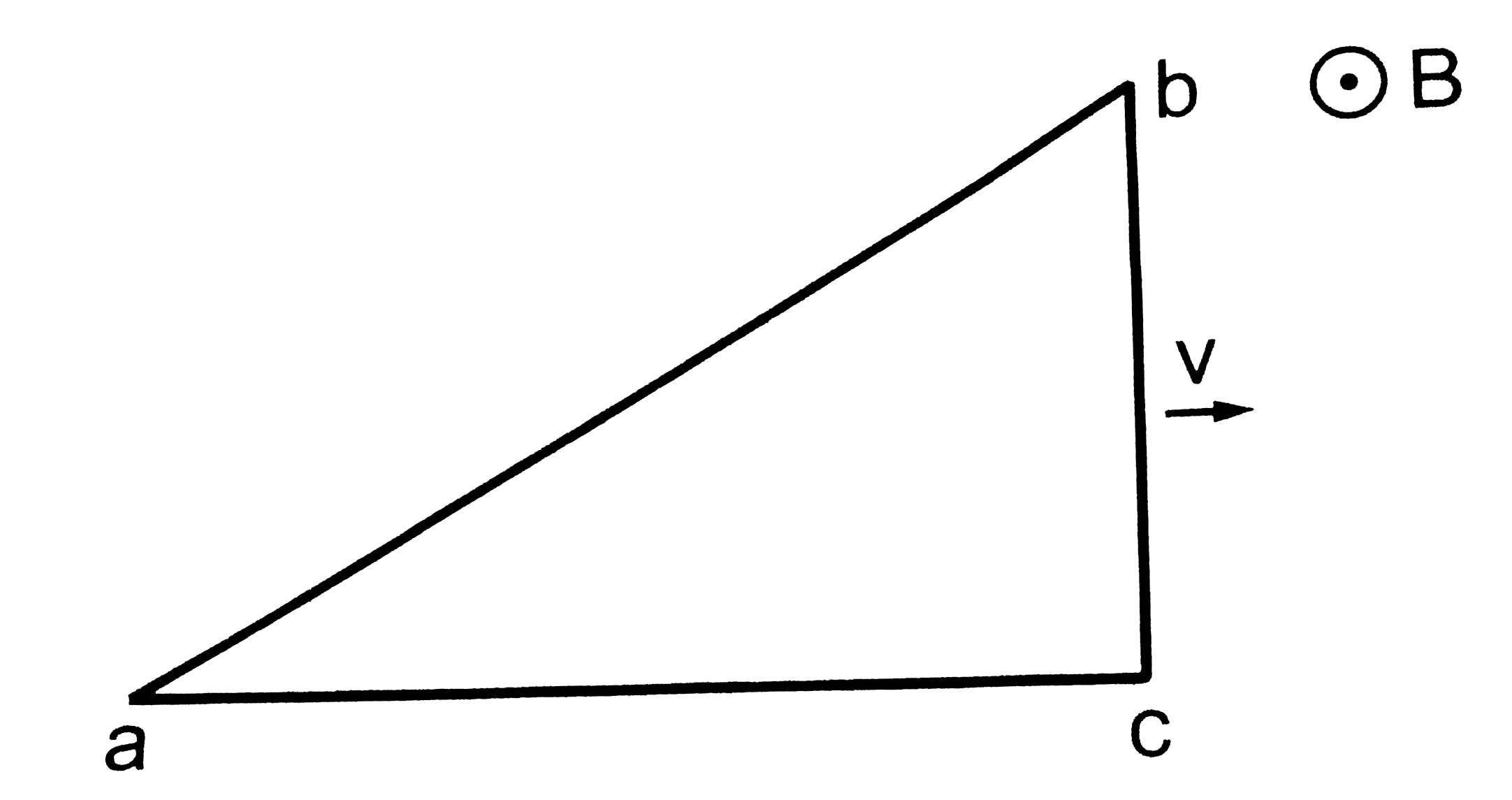
View SolutionA right angled triangle abc, made from a metallic wire, moves at a uniform speed v in its plane as shown in . A uniform magnetic field B exists in the perpendicular direction. Find the emf induced (a) in the loop abc, (b) in the segment bc, (c ) in the segment ac and (d) in the segment ab.
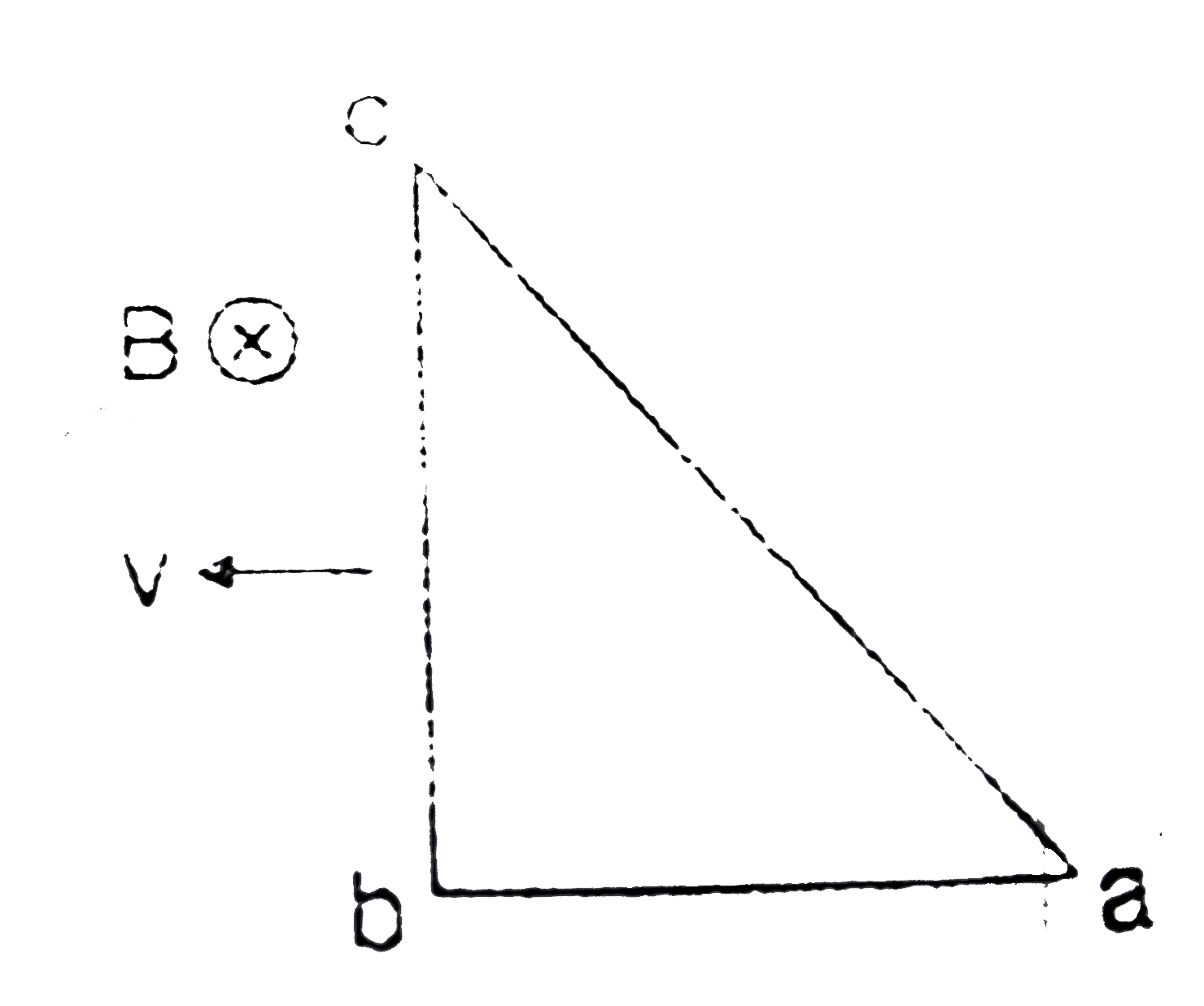
View SolutionA right angled triangle abc made of a metallic wire, moves at a uniform speed v in its plane as shown in the figure.A uniform magnetic field B exists in the perpendicular direction of plane of triangle.Find the emf induced (a)in the loop abc. (b)in the segment bc,(c)in the segment ac and (d) in the segment ab.
View SolutionA copper wire bent in the shape of a semicircle of radius r translates in its plane with a constant velocity v. A uniform magnetic field B exists in the direction perpendicular to the plane of the wire. Find the emf induced between the ends of the wire if (a) the velocity is perpendicular ot the diameter joining free ends, (b) the velocity is parallel to this diameter.
View SolutionA conducting rod of length 1 is moving on a horizontal smooth surface. Magnetic field in the region is vertically downward and magnitude B0. If centre of mass (COM) of the rod is translating with velocity v0 and rod rotates about COM with angular velocity v0/l, then potential difference between points O and A will be
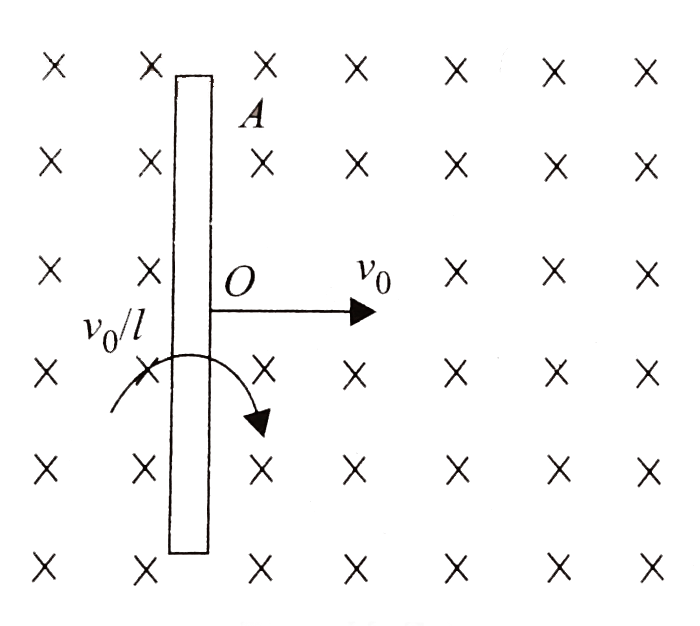
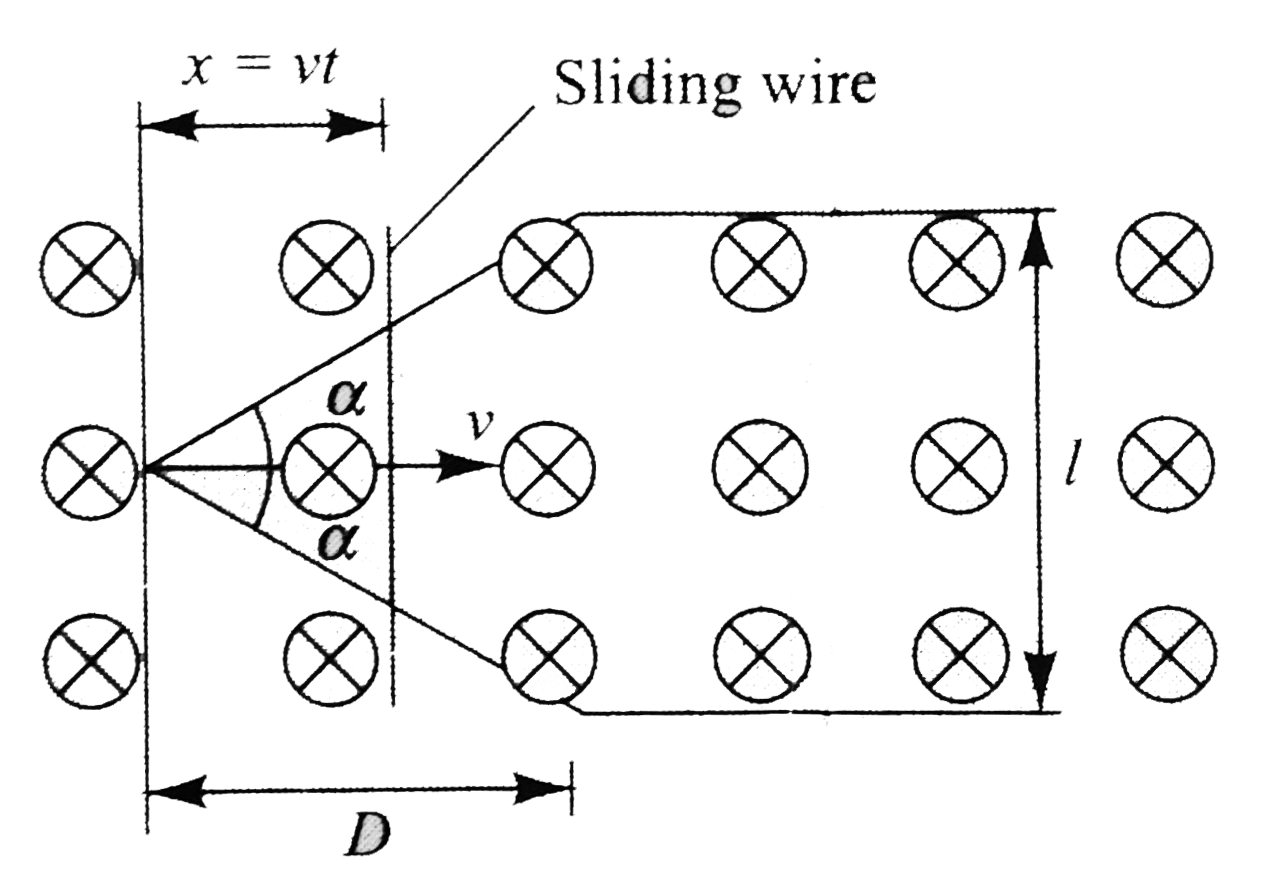
View SolutionConsider the sliding wire circuit shown in . The wire slides at constant speed and the plane of the circuit is perpendicular to a uniform magnetic field. Show that the induced emf is given by E=Blv2t/D foe 0<t<D/v What is the expression for the emf for t>D/v?
View SolutionA conducting rod OA of length l is rotated about its end O with an angular velocity ω in a uniform magnetic field directed perpendicualr to the rotation. Find the emf induced in the rod, between it's ends.
View SolutionFigure shows an irregular shaped wire AB moving with velocity v, as shown. Find the emf induced in the wire
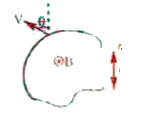
View SolutionA rod of length l is translating at a velocity v making an angle θ with its length. A uniform magnetic field B exists in a direction perpendicular to the plane of motion. Calculate the emf induced In the rod, Draw a figure representing the induced emf by on equivalent battery.


View SolutionA rectangular coil is placed in a region having a uniform magnetic field B perpendicular to the plane of the coil. An emf will not be induced ion the coil if the

View Solution
