A vertical rod of length l is moved with constant velocity v towards east. The vertical component of earth magnetic field is B and angle of dip is . The induced e.m.f. in the rod is
The correct Answer is:C
To find the induced electromotive force (e.m.f.) in a vertical rod of length l that is moved with a constant velocity v towards the east, we will use the principles of electromagnetic induction. The vertical component of the Earth's magnetic field is B, and the angle of dip is θ.
1. Identify the Components of the Magnetic Field:
The Earth's magnetic field can be resolved into two components due to the angle of dip θ:
- The vertical component Bv=Bcos(θ)
- The horizontal component Bh=Bsin(θ)
2. Determine the Horizontal Component:
Since we are interested in the horizontal component of the magnetic field for the induced e.m.f. when the rod moves eastward:
Bh=Bsin(θ)
3. Use the Formula for Induced e.m.f.:
The induced e.m.f. (E) in a rod moving through a magnetic field is given by the formula:
E=Bh⋅l⋅v
where:
- Bh is the horizontal component of the magnetic field,
- l is the length of the rod,
- v is the velocity of the rod.
4. Substituting the Horizontal Component:
Substitute Bh=Bsin(θ) into the e.m.f. formula:
E=(Bsin(θ))⋅l⋅v
5. Final Expression for Induced e.m.f.:
Thus, the induced e.m.f. in the rod can be expressed as:
E=B⋅l⋅v⋅sin(θ)
Conclusion:
The induced e.m.f. in the vertical rod is given by:
E=B⋅l⋅v⋅sin(θ)
The Earth's magnetic field can be resolved into two components due to the angle of dip θ:
- The vertical component Bv=Bcos(θ)
- The horizontal component Bh=Bsin(θ)
Since we are interested in the horizontal component of the magnetic field for the induced e.m.f. when the rod moves eastward:
Bh=Bsin(θ)
The induced e.m.f. (E) in a rod moving through a magnetic field is given by the formula:
E=Bh⋅l⋅v
where:
- Bh is the horizontal component of the magnetic field,
- l is the length of the rod,
- v is the velocity of the rod.
Substitute Bh=Bsin(θ) into the e.m.f. formula:
E=(Bsin(θ))⋅l⋅v
Thus, the induced e.m.f. in the rod can be expressed as:
E=B⋅l⋅v⋅sin(θ)
The induced e.m.f. in the vertical rod is given by:
E=B⋅l⋅v⋅sin(θ)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION - A) (OBJECTIVE TYPE QUESTIONS)
35 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION - B) (OBJECTIVE TYPE QUESTIONS)
25 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - J)
5 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - comprehension
3 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
Similar Questions
Horizontal and vertical components of earth’s magnetic field at a place are equal. The angle of dip at that place is ________.
View SolutionAt a place, the horizontal component of earth's magnetic field is B and angle of dip is 60∘. What is the value of horizontal component of earth's magnetic field at equator?
View SolutionA conducting rod of length l is rotating with constant angular velocity ω about point O in a uniform magnetic field B as shown in the figure . What is the emf induced between ends P and Q ?

View SolutionA copper rod of length l is rotated about one end perpendicular to the uniform magnetic field B with constant angular velocity ω . The induced e.m.f. between its two ends is
View SolutionA metallic rod of length l is rotated at a constant angular speed ω, normal to a uniform magnetic field B. Derive an expression for the current induced in the rod, if the resistance of the rod is R.
View SolutionAt a place, the horizontal component of earth's magnetic field is V and angle of dip is 60∘. What is te value of horizontal component of earth's magnetic field at equator ?
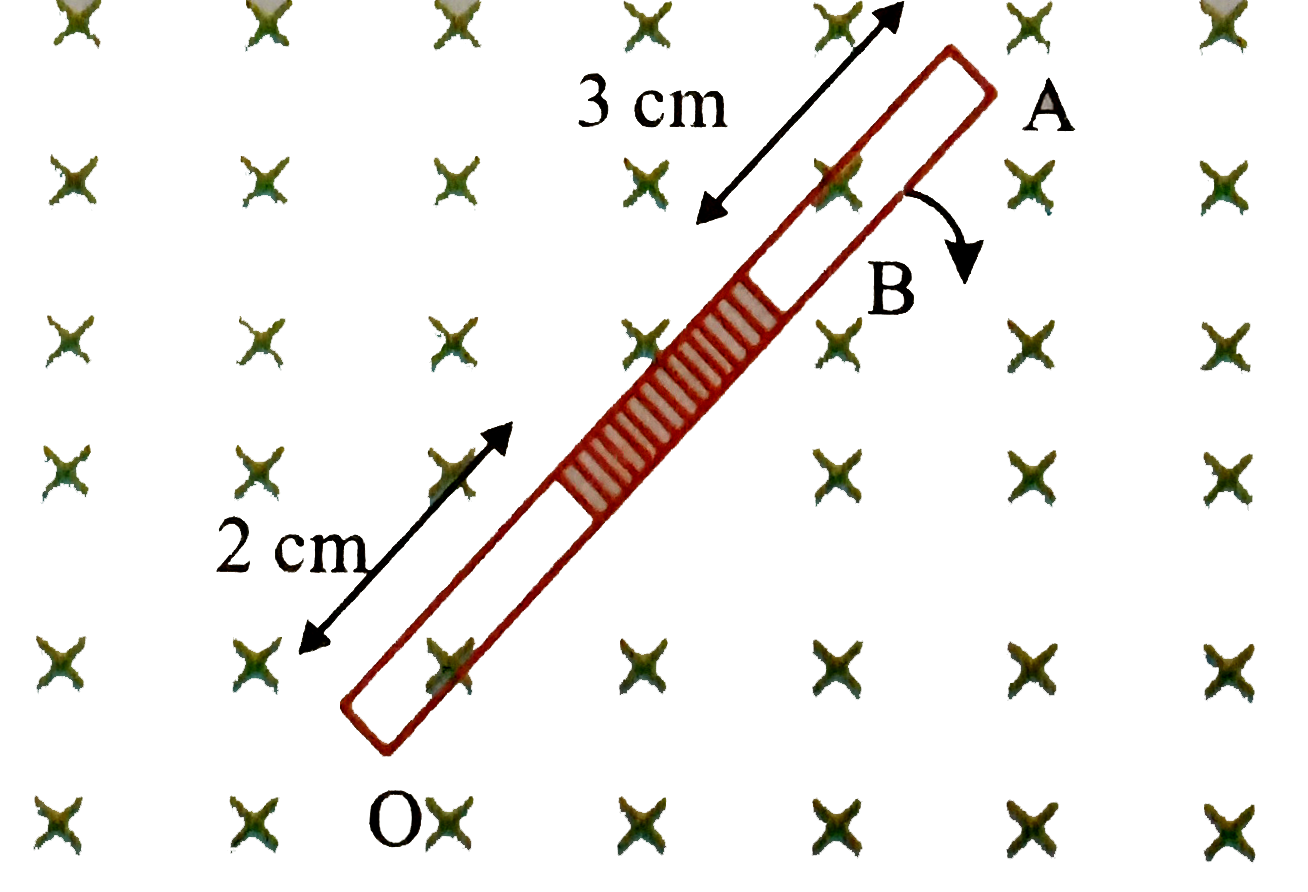
View SolutionA rod of length 10cm made up of conducting and non-conducting material (shaded part is non-conducting). The rod is rotated with constant angular velocity 10rad/s about point O, in constant magnetic field of 2T as shown in the figure. The induced emf between the point A and B of rod will be:
View SolutionAt a perpendicular place on the earth, the horizontal component of earth's magnetic field of B, and the angle of dip is θ. A striaght meridian and is moved horizontally perpendicular to its length with a velocity v. The emf induced across the rod is
View SolutionA copper rod of length l is rotated about one end perpendicular to the magnetic field B with constant angular velocity ω . The induced e.m.f between the two ends is
View SolutionAt a certain place , horizontal component of earth's field is √3 times the vertical component of earth's field . The angle of dip at this place is
View Solution
