A capacitor has capacity C and reactance X. If capacitance and frequency become double, then reactance will be
4X
X2
X4
2X
The correct Answer is:C
To solve the problem, we need to determine how the reactance of a capacitor changes when both its capacitance and the frequency of the AC source are doubled.
1. Understand the formula for capacitive reactance (X):
The reactance XC of a capacitor is given by the formula:
XC=1ωC
where ω=2πf (angular frequency) and C is the capacitance.
2. Identify the changes in capacitance and frequency:
According to the problem, both the capacitance and frequency are doubled:
C′=2Candf′=2f
3. Calculate the new angular frequency:
The new angular frequency ω′ is:
ω′=2πf′=2π(2f)=4πf
4. Substitute the new values into the reactance formula:
Now, we can find the new reactance X′C:
X′C=1ω′C′=1(4πf)(2C)
5. Simplify the expression:
X′C=18πfC
6. Relate the new reactance to the original reactance:
We know that the original reactance XC is:
XC=12πfC
Therefore, we can express the new reactance in terms of the original reactance:
X′C=18⋅12πfC=XC4
7. Conclusion:
Thus, the new reactance X′C when both capacitance and frequency are doubled is:
X′C=XC4
Final Answer:
The reactance will be X4.
---
The reactance XC of a capacitor is given by the formula:
XC=1ωC
where ω=2πf (angular frequency) and C is the capacitance.
According to the problem, both the capacitance and frequency are doubled:
C′=2Candf′=2f
The new angular frequency ω′ is:
ω′=2πf′=2π(2f)=4πf
Now, we can find the new reactance X′C:
X′C=1ω′C′=1(4πf)(2C)
X′C=18πfC
We know that the original reactance XC is:
XC=12πfC
Therefore, we can express the new reactance in terms of the original reactance:
X′C=18⋅12πfC=XC4
Thus, the new reactance X′C when both capacitance and frequency are doubled is:
X′C=XC4
The reactance will be X4.
Similar Questions
Knowledge Check
In a pure capacitive circuit if the frequency of ac source is doubled, then its capacitive reactance will be
Aremains sameBdoubledChalvedDzero
If each capacitor has capacitance C, then equivalent capacitance between A and B is

View SolutionFind capacitive reactance of a capacitor connected to a dc source.
View SolutionThe capacitive reactance in an A.C. circuit is
View SolutionWith increase in frequency of an AC supply, the inductive reactance:
View SolutionEach capacitor has cpacitance C.
 .
.
The equivalent capacitance between 4 and 5 is .
View SolutionThe figure shows the graphical variation of the reactance of a capacitor with frequency of ac source. (a) find the capacitance of the capacitor (b)an ideal inductor has the same reactance at 100 Hz frequency as the capacitor has the same frequency find the value of the inductor. (c) draw the graph showing the variation of the reactance of this inductor with frequency

View SolutionIn the arrangement of the capacitor shown in the figure, each C1 capacitor has capacitance of 3μF and each C2 capacitor has capacitance of 2μF then,
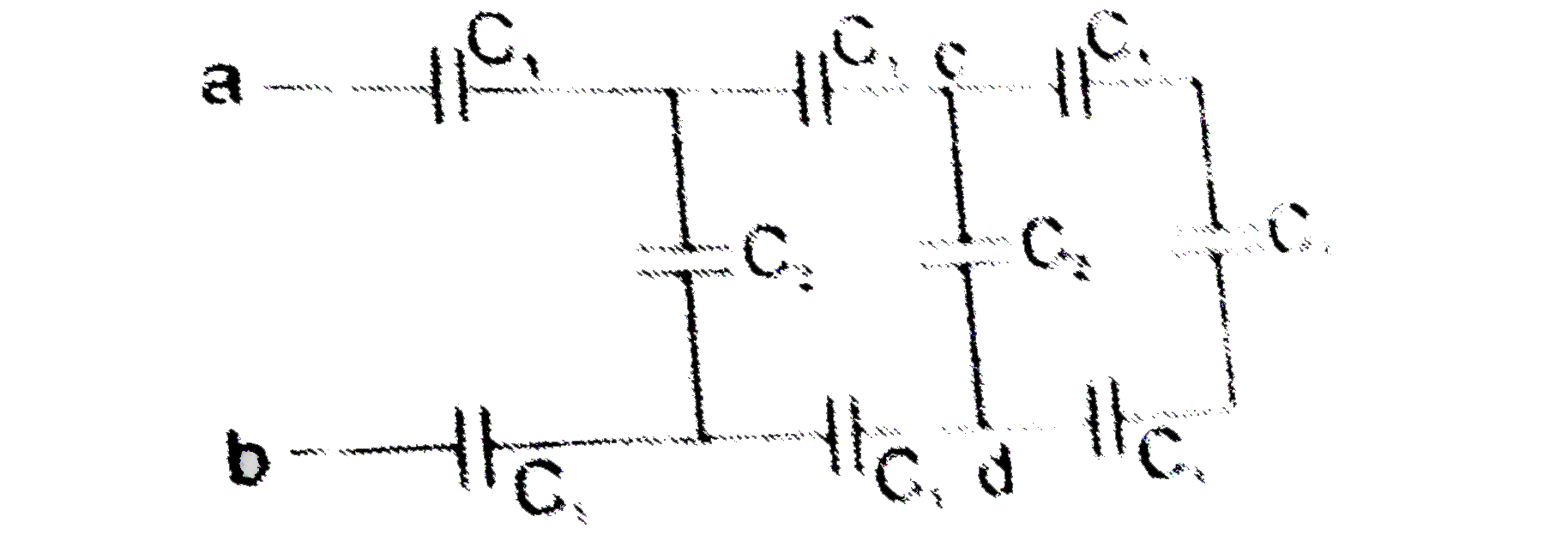
(i) Equivalent capacitance of the network between the points a and b is :
View Solution

 .
.