According to Ampere's circuital law
∮¯¯¯B.¯¯¯¯dI=μ0(iC+ε0dϕEdt)
∮¯¯¯B.¯¯¯¯dI=μ0ε0dϕEdt
∮¯¯¯B.¯¯¯¯dI=μ0ε0i
∮¯¯¯B.¯¯¯¯dI=μ0(iCdϕEdt+iO)
The correct Answer is:A
Step by step video & image solution for According to Ampere's circuital law by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - B Objective Type Questions
10 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - C Previous Years Questions
22 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION -D) Assertion-Reason type Question)
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
9 Videos
Similar Questions
Ampere's circuital law is given by
View SolutionState Ampere.s circuital law.
View SolutionWhich of the following ares assorciated with Maxwell ?
a. Displacement current
(b) Unification of the laws of elecriciry and magnestism
(c) Development of Ampere's circuital law
(d) Velocity distribuation of molecues in gas
(e) Modification of Ampere's law
View SolutionWrite equation for Ampere's circuital law for the Amperial loop as shown below
(Traverse in the direction shown by arrow mark buton it )
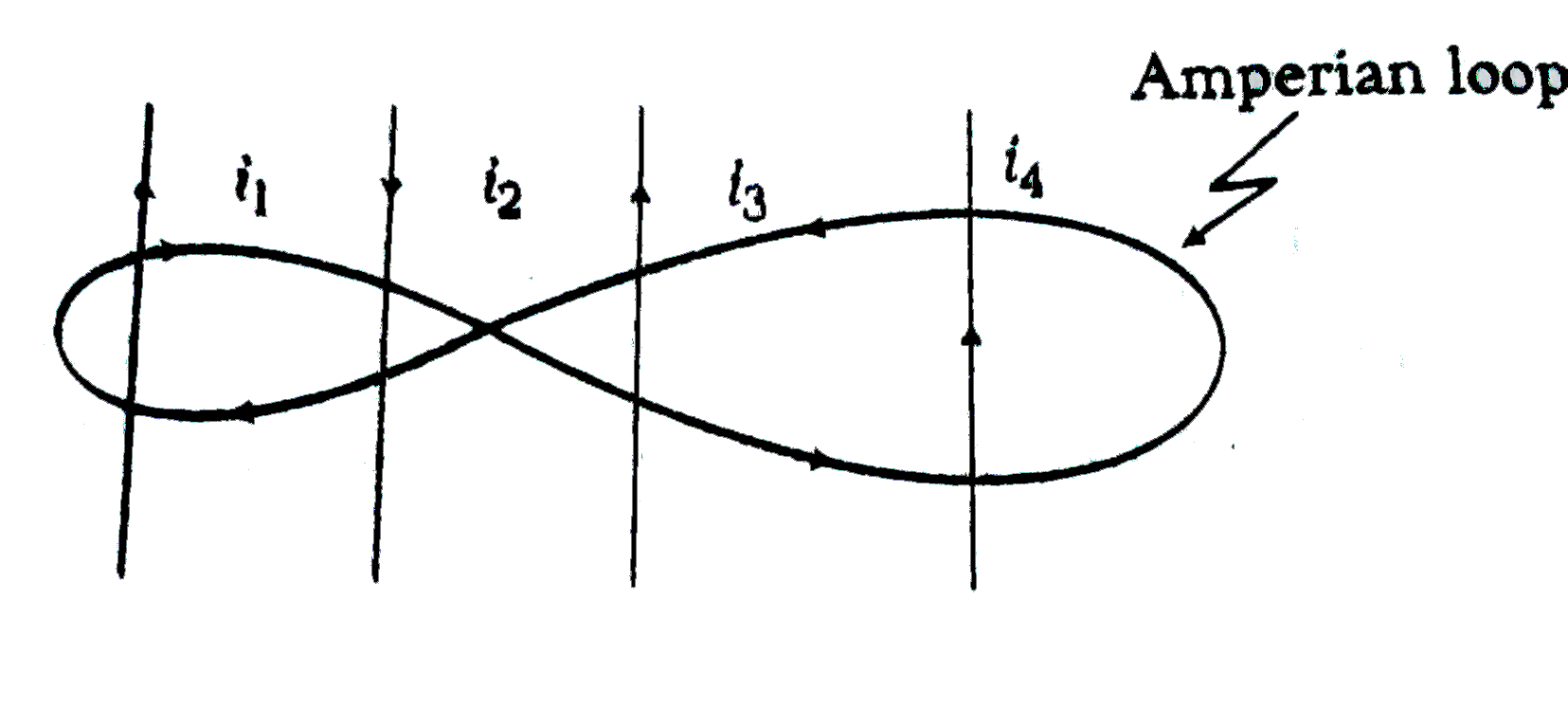
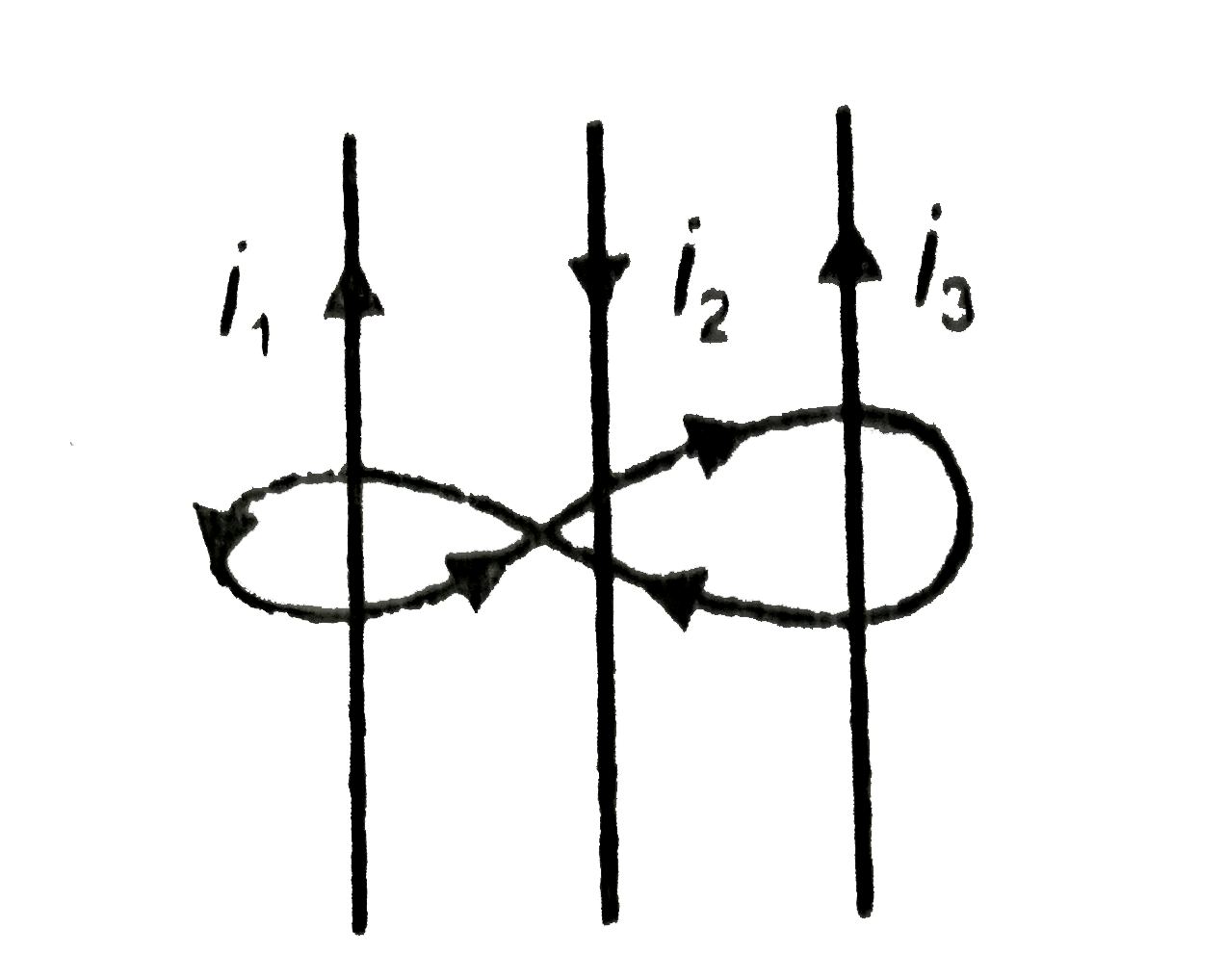
View SolutionWrite equation for Ampere's circuital law for the Amperian loop shown (traversed in the direction shown by arrow marks put on it)
View Solutionwrite the expression for the generalized form of Ampere's circuital law. Discuss its significance and describe briefly how the concept of dislacement current is explained through charing/discharging of a capacitor in an electric circuit.
View SolutionA long straight wire of a circular cross-section of radius 'a' carries a steady current I. The current is uniformly distributed across the cross-section. Apply Ampere's circuital law to calculate the magnetic field at a point at distance 'r' in the region for (i) r<a and (ii) r>a.
View Solution(A) : The magnetic field at the centre of a circular coil carrying current could be calculated using Amperes law.
(R) : Biot savart law could be derived from Amperes law.
View SolutionConsidering the case of a parallel plate capacitor being charged, show how one is required to generalize Ampere's circuital law to include the term due to displacment current.
View SolutionAccording to Wien's law
View Solution
