If the electric field and magnetic field of an electromagnetic wave are related as B=Ec where the symbols have their usual meanings and the energy in a given volume of space due to the electric field part is U, then the energy due to the magnetic field part will be
Uc
Uc2
U2
U
The correct Answer is:D
To solve the problem, we need to find the energy due to the magnetic field part of an electromagnetic wave, given that the energy due to the electric field part is U.
1. Understanding the Relationship:
We know that the magnetic field B is related to the electric field E by the equation:
B=Ec
where c is the speed of light.
2. Energy in Electric Field:
The energy density UE (energy per unit volume) in the electric field is given by:
UE=12ϵ0E2
where ϵ0 is the permittivity of free space.
3. Energy in Magnetic Field:
The energy density UB in the magnetic field is given by:
UB=12B2μ0
where μ0 is the permeability of free space.
4. Substituting for B:
We can substitute the expression for B into the equation for UB:
UB=12(B)2μ0=12(Ec)2μ0
This simplifies to:
UB=12E2c2μ0
5. Using the Relationship between c, μ0, and ϵ0:
We know that:
c=1√μ0ϵ0⟹c2=1μ0ϵ0
Therefore, we can replace c2 in our expression for UB:
UB=12E21μ0ϵ0=12μ0ϵ0E2
6. Relating UB to U:
Since we already have the expression for UE:
UE=12ϵ0E2
We can see that:
UB=12μ0ϵ0E2=UE
Thus, we find that:
UB=U
Final Answer:
The energy due to the magnetic field part will be equal to U.
---
We know that the magnetic field B is related to the electric field E by the equation:
B=Ec
where c is the speed of light.
The energy density UE (energy per unit volume) in the electric field is given by:
UE=12ϵ0E2
where ϵ0 is the permittivity of free space.
The energy density UB in the magnetic field is given by:
UB=12B2μ0
where μ0 is the permeability of free space.
We can substitute the expression for B into the equation for UB:
UB=12(B)2μ0=12(Ec)2μ0
This simplifies to:
UB=12E2c2μ0
We know that:
c=1√μ0ϵ0⟹c2=1μ0ϵ0
Therefore, we can replace c2 in our expression for UB:
UB=12E21μ0ϵ0=12μ0ϵ0E2
Since we already have the expression for UE:
UE=12ϵ0E2
We can see that:
UB=12μ0ϵ0E2=UE
Thus, we find that:
UB=U
The energy due to the magnetic field part will be equal to U.
Topper's Solved these Questions
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - C Previous Years Questions
22 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - A Objective Type Questions
25 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION -D) Assertion-Reason type Question)
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
9 Videos
Similar Questions
The electric and magnetic field of an electromagnetic wave is
View SolutionElectric field induced by changing magnetic fields are
View SolutionMagnetic field at the centre O due to the given structure is
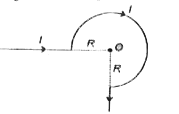
View SolutionElectric Field due to Dipole
View SolutionThe amplitudes of electric and magnetic fields are related to each other as
View SolutionWrite the dimensions of EB. Here, E is the electric field and B the magnetic field.
View SolutionDiscuss the similarities between the energy stored in the electric field of charged capacitor and the energy stored in the magnetic field of a current-carrying coil.
View SolutionMagnetic field at point O due to the given structure is
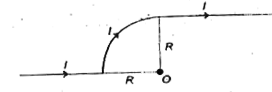
View SolutionShow that the avearge energy density of the electric field →E equals the average energy density of the magnetic field →B, in electromagnetic waves.
View SolutionIn an electromagnetic wave in free space the root mean square value of the electric field is Erms=6V/m. The peak value of the magnetic field is
View Solution
