What is the shape of the wavefront in each of the following cases ?
Light emerging out of a convex lens when a point source is placed at its focus.
To determine the shape of the wavefront when light emerges from a convex lens with a point source placed at its focus, we can follow these steps:
1. Understand the Setup:
- We have a convex lens and a point source of light placed at its focus.
2. Behavior of Light Rays:
- When light rays emanate from the point source located at the focus of the convex lens, these rays converge towards the lens and then refract through it.
3. Refraction Through the Lens:
- The convex lens causes the light rays that are initially diverging from the point source to refract and emerge parallel to the principal axis of the lens. This is a key property of convex lenses.
4. Definition of Wavefront:
- A wavefront is defined as the locus of all points that are in the same phase of the wave. For light waves, this means all points on the wavefront are at the same stage of their oscillation.
5. Shape of the Wavefront:
- Since the light rays emerge parallel after passing through the lens, the wavefront formed is a plane wavefront. In two dimensions, this can be visualized as a straight line, while in three dimensions, it is represented as a flat plane.
6. Conclusion:
- Therefore, the shape of the wavefront when light emerges from a convex lens with a point source at its focus is a plane wavefront.
Final Answer:
The shape of the wavefront is a plane wavefront.
- We have a convex lens and a point source of light placed at its focus.
- When light rays emanate from the point source located at the focus of the convex lens, these rays converge towards the lens and then refract through it.
- The convex lens causes the light rays that are initially diverging from the point source to refract and emerge parallel to the principal axis of the lens. This is a key property of convex lenses.
- A wavefront is defined as the locus of all points that are in the same phase of the wave. For light waves, this means all points on the wavefront are at the same stage of their oscillation.
- Since the light rays emerge parallel after passing through the lens, the wavefront formed is a plane wavefront. In two dimensions, this can be visualized as a straight line, while in three dimensions, it is represented as a flat plane.
- Therefore, the shape of the wavefront when light emerges from a convex lens with a point source at its focus is a plane wavefront.
The shape of the wavefront is a plane wavefront.
Similar Questions
What is the shape of the wavefront in each of the following cases ?
Light diverging from a point source.
View SolutionWhat is the shape of the wavefront diverging from a point source of light?
View SolutionA : The geometrical shape of the wave front when a wavefront passes through a convex lens will be again plane wave front
R : Whne a plane wave front is reflected by a concave mirror, it remains as plane wavefront.
View SolutionAn object is placed at a distance of 15cm from a convex lenx of focal length 10cm. On the other side of the lens, a convex mirror is placed at its focus such that the image formed by the combination coincides with the object itself. The focal length of the convex mirror is
View SolutionHuygen was the first scientist who proposed the idea of wave theory of light. He said that the light propagates in form of wavefronts. A wavefront is an imaginary surface at every point of which waves are in the same phase. For example the wavefronts for a point source of light is collectionof concentric spheres which have centre at the origin. w1 is a wavefront. w2 is another wavefront.

The redius of the wavefront at time 't' is 'ct' in this case where 'c' is the speed of light. The direction of propagation of light is perpendicular to the surface of the wavefront. The wavefronts are plane wavefronts in case of a parallel beam of light.

Huygen also said that every point of the wavefront acts as the source of secondary wavelets. The tangent drawn to all secondary wavelets at a time is the new wavefront at that time. The wavelets are to be consid-ered only in the forward direction (i.e. the direction of propagation of light) and not in the reverse direction. If a wavefront w1 at time t is given, then to draw the wavefront at time t+Δt0 take some points on the wavefront w1 and draw spheres of radius 'cΔt'. They are called secondary wavelets
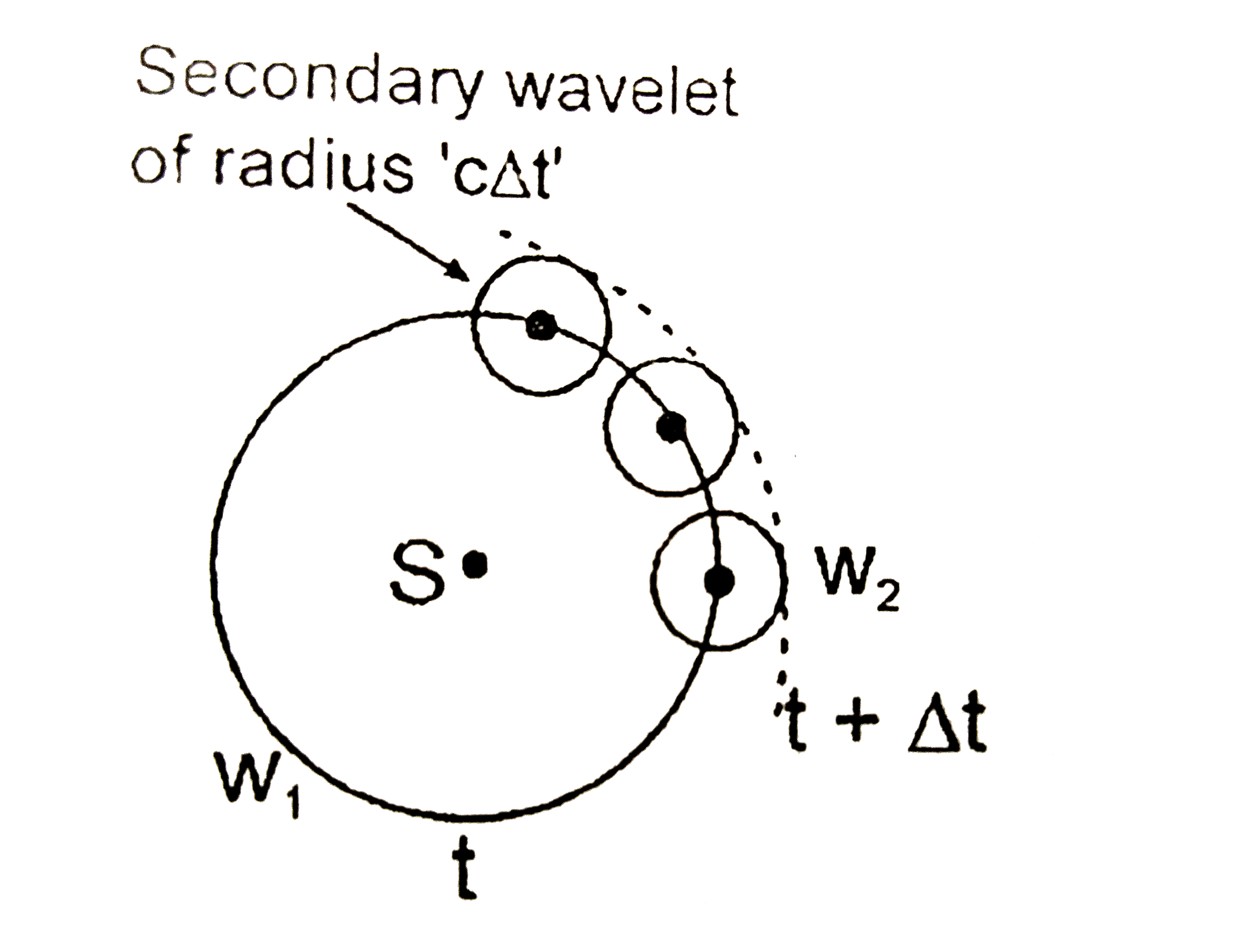
Draw a surface w2 which is tangential to all these secondary wavelets. w2 is the wavefront at time 't+Δt'. Huygen proved the laws of reflection and laws of refraction using concept of wavefronts.
A point source of light is placed at origin, in air. The equation of wave front of the wave at time t, emitted by source at t=0, is (take refractive index of air as 1)
View SolutionA thin equiconvex glass lens (μg=1.5) is beign placed on the top of a vessel of height h=20cm as shown figure. A luminous point source is beign placed at the bottom of vessel on the principal axis of the lens. When the air is on both the side of the lens the image of luminous source is formed at a distance of 20cm from the lens out side the vessel. When the air inside the vessel is being replaced by a liquid of refractive index μl the image of the same source is being formed at a distance 30cm from the lens outside the vessel. Find the μl.

View Solution(i) Define term wavefront. State Huygen.s principle.
(ii) consider a plane wavefront incident on a thin convex lens. Draw a proper diagram to show him the incident wavefront traverses throught the lens and after refraction focuses on the focal point of the lens, giving the shape of the emergent wavefront.
(iii) When light travels from a rarer to a denser medium, it loses speed. Does, this loss imply a reduction in energy carried by the light waves.
View SolutionA converging lens and a diverging mirror are placed at a separation of 15 cm. The focal length of the lens is 25 cm and that of the mirror is 40 cm. Where should a point source be placed between the lens and the mirror so that the light, after getting reflected by the mirror and then getting transmitted by the lens, comes out parallel to the principal axis ?
View SolutionA converging lens and a diverging mirror are placed at a separation of 20 cm. The focal length of the lens is 30 cm and that of the mirror is 50 cm. Where should a point source be placed between the lens and the miror, so that the light, after getting reflected by the mirror and then getting transmitted by the lens, comes out parallel to the principal axis?
View SolutionA glass wedge with a small angle of refraction θ is placed at a certain distance from a converging lens with a focal length f ,one surface of the wedge being perpendicular to the optical axis of the lens. A point sources S of light is on the other side of the lens at its focus. The rays reflected from the wedge (not from base) produce, after refraction in the lens , two images of the source displaced with respect to each other by d. Find the refractive index of the wedge glass. [Consider only paraxial rays.]
_E01_162_Q01.png)
View Solution
