A: When a tiny circular obstacle is placed in the path of light from a distant source, a bright spot is seen at the centre of the shadow of the obstacle.
R: Waves diffracted from the edge of the circular obstacle interfere constructively at the centre of the shadow producing a bright spot.
IF both Assertion & Reason are true and the reason is the correct explanation of the assertion, then mark (1).
If both Assertion & Reason are true but the reason is not the correct explanation of the assertion, then mark(2)
IF Assertion is true statement but Reason is false then mark(3)
If both Assertion and Reason are false statements, then mark (4)
The correct Answer is:A
To solve the assertion and reason question, we will analyze both statements step by step.
Step 1: Understanding the Assertion
The assertion states that when a tiny circular obstacle is placed in the path of light from a distant source, a bright spot is seen at the center of the shadow of the obstacle.
Explanation:
- When light from a distant source (which can be considered as plane waves) encounters a small circular obstacle, it creates a shadow region behind the obstacle.
- However, due to the phenomenon of diffraction, light waves bend around the edges of the obstacle.
Step 2: Understanding the Reason
The reason states that waves diffracted from the edge of the circular obstacle interfere constructively at the center of the shadow, producing a bright spot.
Explanation:
- As the light waves bend around the edges of the circular obstacle, they spread out and overlap.
- At the center of the shadow, the waves from the edges of the obstacle meet in phase (i.e., they are aligned), which leads to constructive interference.
- Constructive interference occurs when the crest of one wave aligns with the crest of another wave, resulting in an increase in intensity, hence creating a bright spot.
Step 3: Conclusion
Both the assertion and the reason are true. The reason correctly explains the assertion because the bright spot at the center of the shadow is indeed due to the constructive interference of the diffracted waves from the edges of the circular obstacle.
Final Answer:
Both the assertion and the reason are true, and the reason is a correct explanation for the assertion.
---
The assertion states that when a tiny circular obstacle is placed in the path of light from a distant source, a bright spot is seen at the center of the shadow of the obstacle.
- When light from a distant source (which can be considered as plane waves) encounters a small circular obstacle, it creates a shadow region behind the obstacle.
- However, due to the phenomenon of diffraction, light waves bend around the edges of the obstacle.
The reason states that waves diffracted from the edge of the circular obstacle interfere constructively at the center of the shadow, producing a bright spot.
- As the light waves bend around the edges of the circular obstacle, they spread out and overlap.
- At the center of the shadow, the waves from the edges of the obstacle meet in phase (i.e., they are aligned), which leads to constructive interference.
- Constructive interference occurs when the crest of one wave aligns with the crest of another wave, resulting in an increase in intensity, hence creating a bright spot.
Both the assertion and the reason are true. The reason correctly explains the assertion because the bright spot at the center of the shadow is indeed due to the constructive interference of the diffracted waves from the edges of the circular obstacle.
Both the assertion and the reason are true, and the reason is a correct explanation for the assertion.
Similar Questions
A : When tiny circular obstacle is placed in the path of light from some distance, a bright spot is seen at the centre of the shadow of the obastacle.
R : Destructive interference occurs at the centre of the shadow of circular obstacle.
View SolutionIn a singleslit diffraction experiment, when a tiny circular obstacle is placed in the path of light from a distant source, a bright spot is seen at the centre of the shadow of the obstacle. Explain why ?
State two points of difference the interference pattern obtained in Young's double slit experiment and the diffraction pattern due to a single slit.
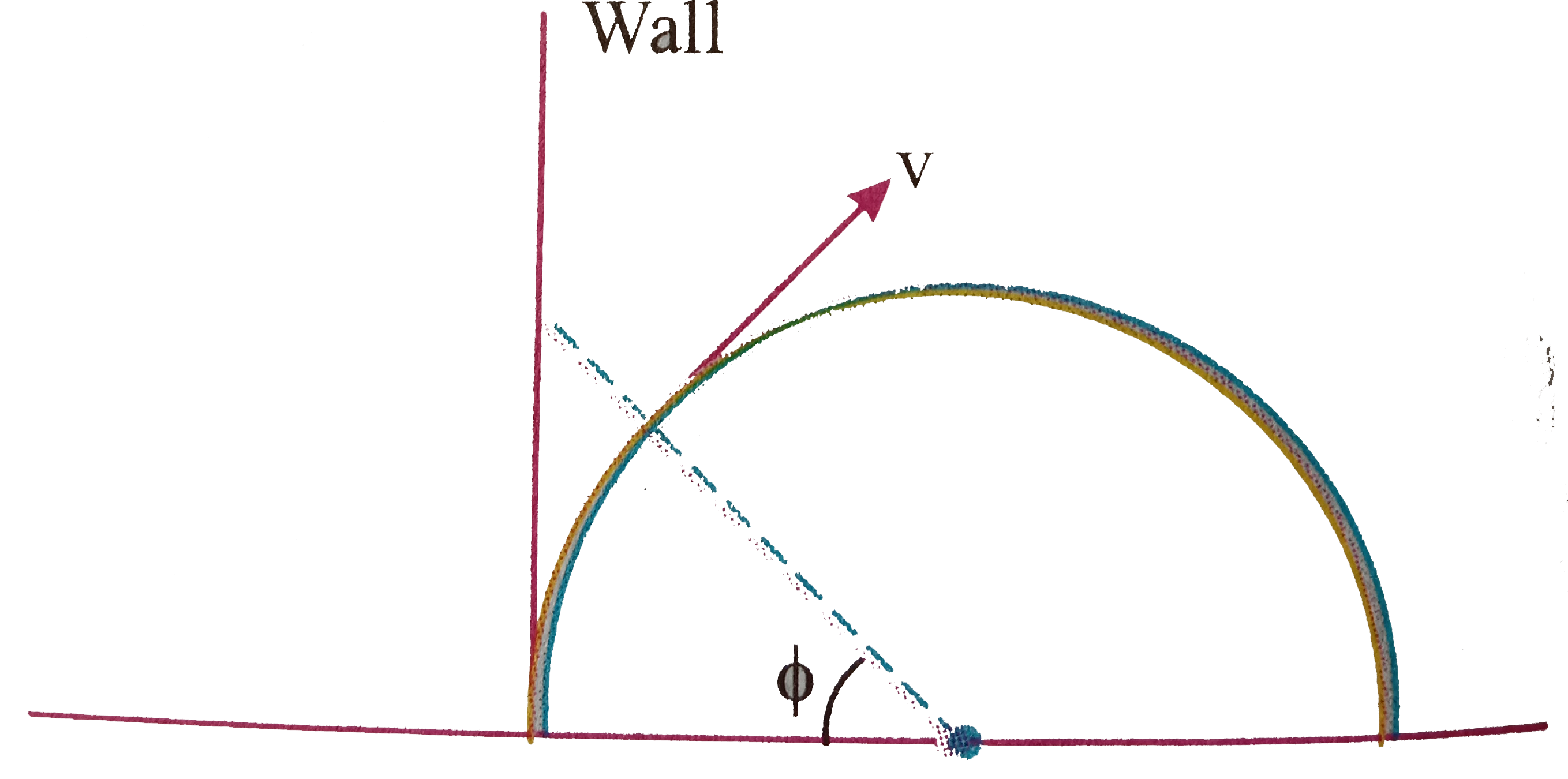
View SolutionOn a particle moving on a circular path with constant speed v, light is thrown from a projectors placed at the centre of the circular path. The shadow of the particle is formed on the wall. The velocity of shadow up the wall is
View Solution(a) Define a wavefront. Using Huygen's principle, verify the laws of reflection at a plane surface .
(b) In a single slit diffraction experiment the wildth of the slit is made double the orignal width.
How does this affect the size and intensity of the central diffraction band ? Explain.
(c) When a tiny circular obstacle in placed in the path of light from a distance source, a bright spot is seen at the centre of the obstacle . Explain why.
View SolutionA student is studying a book placed near the edge of a circular table of radius R. A point source of light is suspended directly above the centre of the table. What should be the height of the source above the table so as to produce maximum illuminance at the position of the book ?
View SolutionA large glass slab (μ=5/3) of thickness 8cm is placed over a point source of light on a plane surface. It is seen that light emerges out of the top surface of the slab from a circular area of radius R cm. What is the value of R?
View SolutionLight of wavelength λ from a point source falls on a small circular rings around a central bright spot are formed on a screen beyond the obstacle The distance between the screen and obstacle is D. Then, the condition for the formation of rings, is
View SolutionThe red light of wavelength 5400 Å from a distant source falls on a slit 0.80 mm wide. Calculate the distance between the first two dark bands on each side of the central bright band in the diffraction pattern observed on a screen place 1.4m from the slit.
View SolutionAs shown, a narrow beam of light is incident onto a semi-circular glass cylinder of radius R. Light can exit the cylinder when the beam is at the centre. When the beam is moved parallel to a maximum distance d from the central line, no light can exit the cylinder from its lower surface. Find the refractive index of the glass.
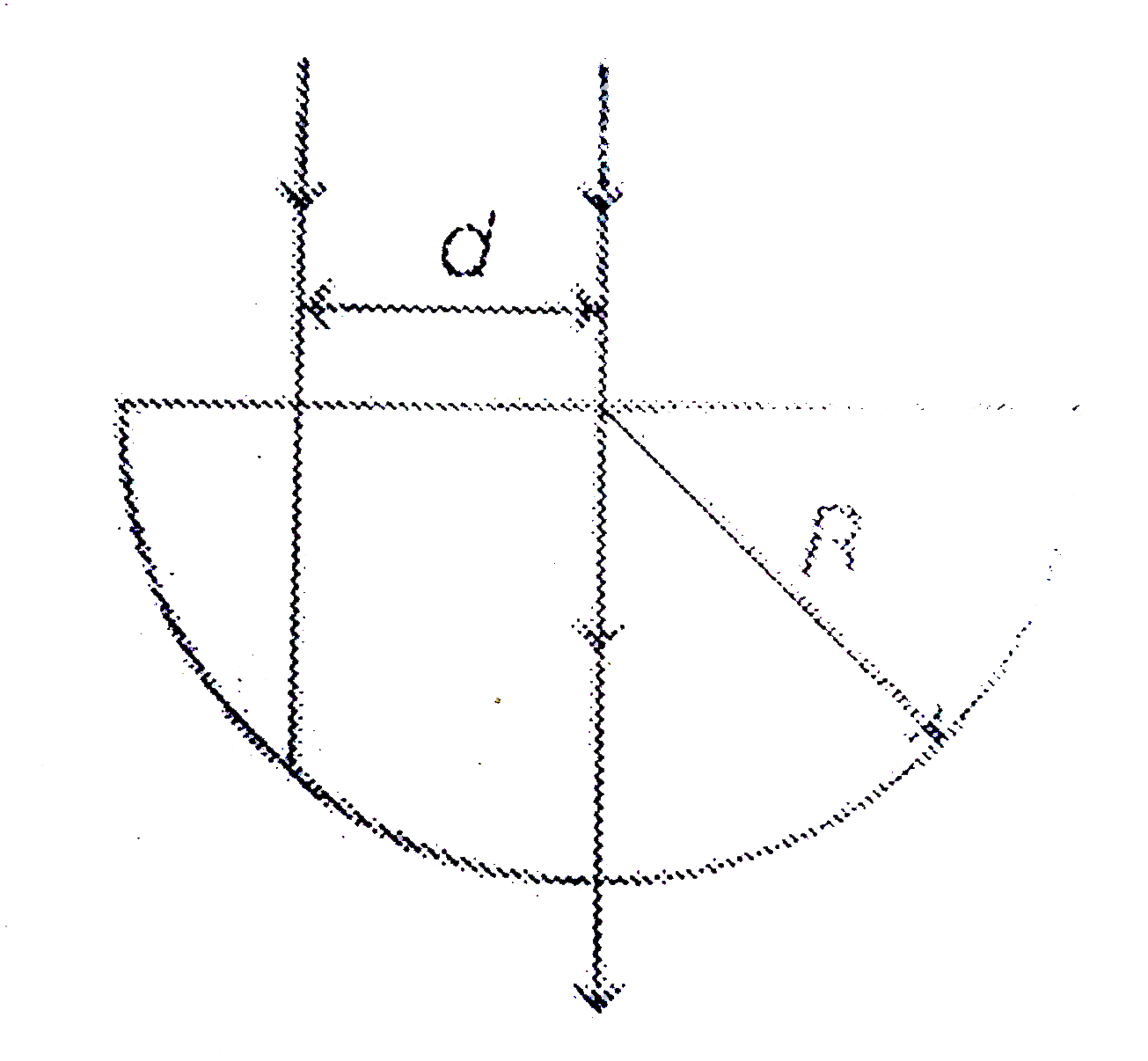
View SolutionThe figure shows a circular loop of radius a with two long parallel wires (numbered 1 and 2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
(q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions.
(r) There is no magnetic field at P.
(s) The wires repel each other.
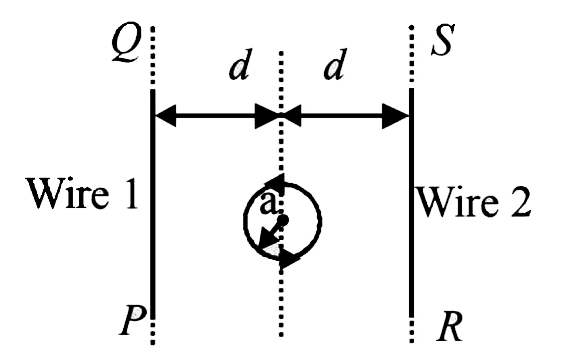
(4) When d≈a but wires are not touching the loop , it is found that the net magnetic field on the axis of the loop . In that case
View Solution
