A photo-cell is illuminated by a source of light which is placed at a distance d from the cell . If the distance become d/2 . Then number of electrons emitted per seconed will be
Remain same
Four times
Two times
One-fourth
The correct Answer is:B
To solve the problem, we will analyze how the change in distance from the light source affects the number of electrons emitted from the photocell.
1. Understanding the relationship between intensity and distance:
- The intensity I of light from a point source is inversely proportional to the square of the distance d from the source. Mathematically, this can be expressed as:
I∝1d2
2. Initial and final distances:
- Let the initial distance from the light source to the photocell be d.
- When the distance is changed to d2, we need to find the new intensity I2 at this new distance.
3. Calculating the intensities:
- The initial intensity I1 at distance d can be represented as:
I1∝1d2
- The new intensity I2 at distance d2 is:
I2∝1(d2)2=1d24=4d2
4. Finding the ratio of intensities:
- Now, we can find the ratio of the two intensities:
I1I2=1d24d2=14
- This implies:
I2=4I1
5. Relating intensity to the number of emitted electrons:
- The number of electrons emitted per second from the photocell is directly proportional to the intensity of the light incident on it:
N∝I
- Therefore, if the intensity increases to 4I1, the number of electrons emitted N2 at the new intensity will be:
N2=4N1
- Here, N1 is the number of electrons emitted at the initial intensity I1.
6. Conclusion:
- Thus, when the distance is reduced from d to d2, the number of electrons emitted per second becomes four times the initial number of electrons emitted.
Final Answer:
The number of electrons emitted per second will be 4N1, where N1 is the initial number of electrons emitted.
---
- The intensity I of light from a point source is inversely proportional to the square of the distance d from the source. Mathematically, this can be expressed as:
I∝1d2
- Let the initial distance from the light source to the photocell be d.
- When the distance is changed to d2, we need to find the new intensity I2 at this new distance.
- The initial intensity I1 at distance d can be represented as:
I1∝1d2
- The new intensity I2 at distance d2 is:
I2∝1(d2)2=1d24=4d2
- Now, we can find the ratio of the two intensities:
I1I2=1d24d2=14
- This implies:
I2=4I1
- The number of electrons emitted per second from the photocell is directly proportional to the intensity of the light incident on it:
N∝I
- Therefore, if the intensity increases to 4I1, the number of electrons emitted N2 at the new intensity will be:
N2=4N1
- Here, N1 is the number of electrons emitted at the initial intensity I1.
- Thus, when the distance is reduced from d to d2, the number of electrons emitted per second becomes four times the initial number of electrons emitted.
The number of electrons emitted per second will be 4N1, where N1 is the initial number of electrons emitted.
Topper's Solved these Questions
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Try Yourself
15 Videos
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Assignment (Section - A) ( Objective Type Questions ( One option is correct))
40 Videos
- ATOMSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ATOMSEXERCISE - ASSIGNMENT SECTION J (Aakash Challengers )
5 Videos
Similar Questions
A photocell is illuminated by a small bright source places 1 m away when the same source of light is placed 12 m away. The number of electron emitted by photocathode would be
View SolutionA photo cell is receiving light from a source placed at a distance of 1m. If the same source is to be placed at a distance of 2m , then the ejected electron
View SolutionA photo cell is illuminated by a small bright source placed 1m away When the same source of light is placed 2m away, the electrons emitted by photo cathode
View SolutionA point source of light is placed at a distance of 2f from a converging lens of focal length f. The intensity onteh other side of the lens is maximum at a distance
View SolutionIn a concave mirror, an object is placed at a distance d1 from the focus and the real image is formed aat a distance d2 from the focus. Then the focal length of the mirror is :
View SolutionThe distance between two coherent sources is 1 mm. The screen is placed at a distance of 1 m from the sources. If the distance of the third bright fringe is 1.2 mm from the central fringe, the wavelength of light used is
View SolutionA lens of focal length 20.0 cm and aperture radius 2.0cm is placed at a distance 30.cm from a point source of light. On the other side a screen is placed at a distance 50.0cm from the lens. The radius of spot of light formed on screen is (neglect spherical abberation through lens)
View SolutionTwo coherent narrow slits emitting light of wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ. The light is collected on a screen S which is placed at a distance D(gtgtλ) from the slit S1 as shown in figure. Find the finite distance x such that the intensity at P is equal to intensity O.
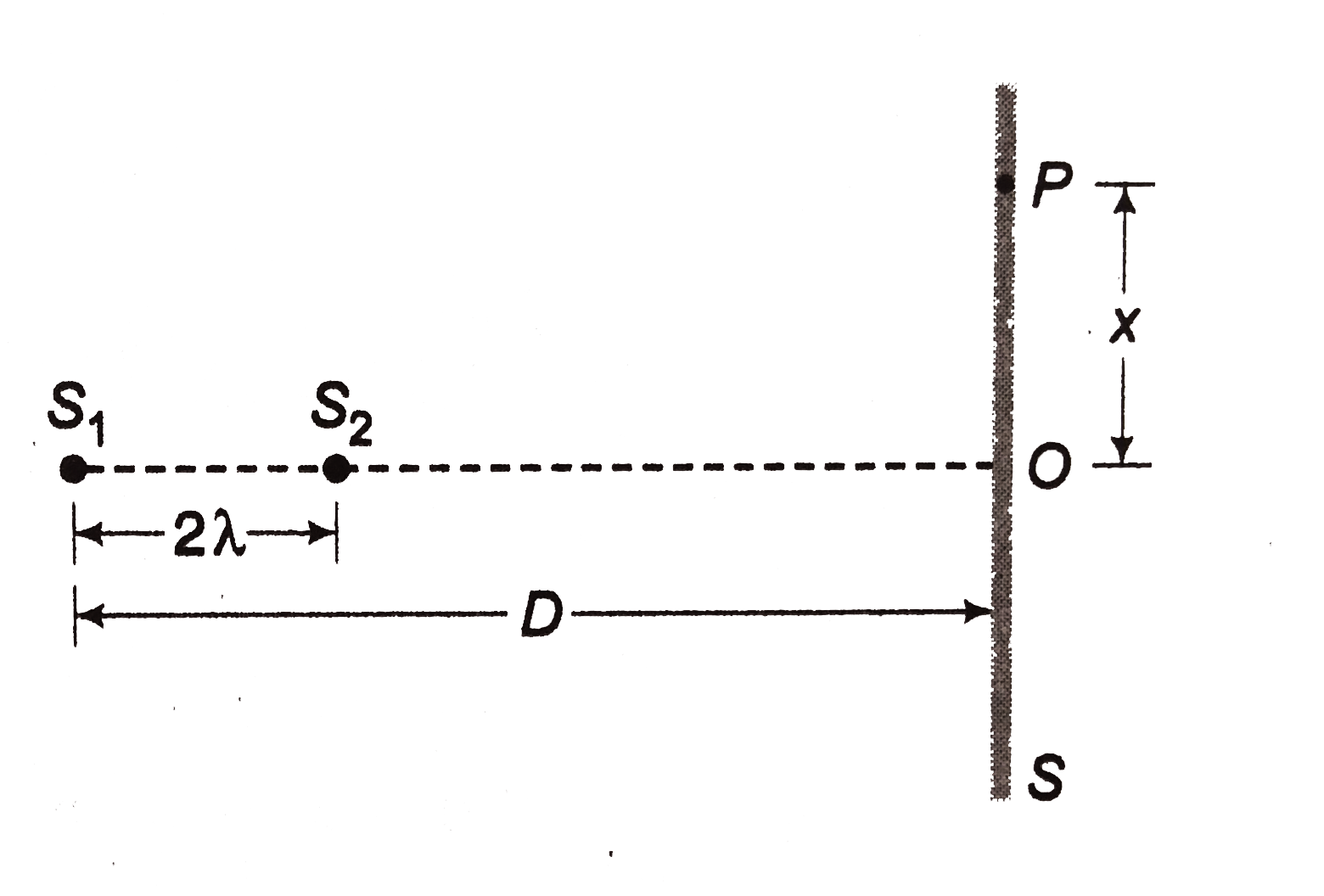 .
.
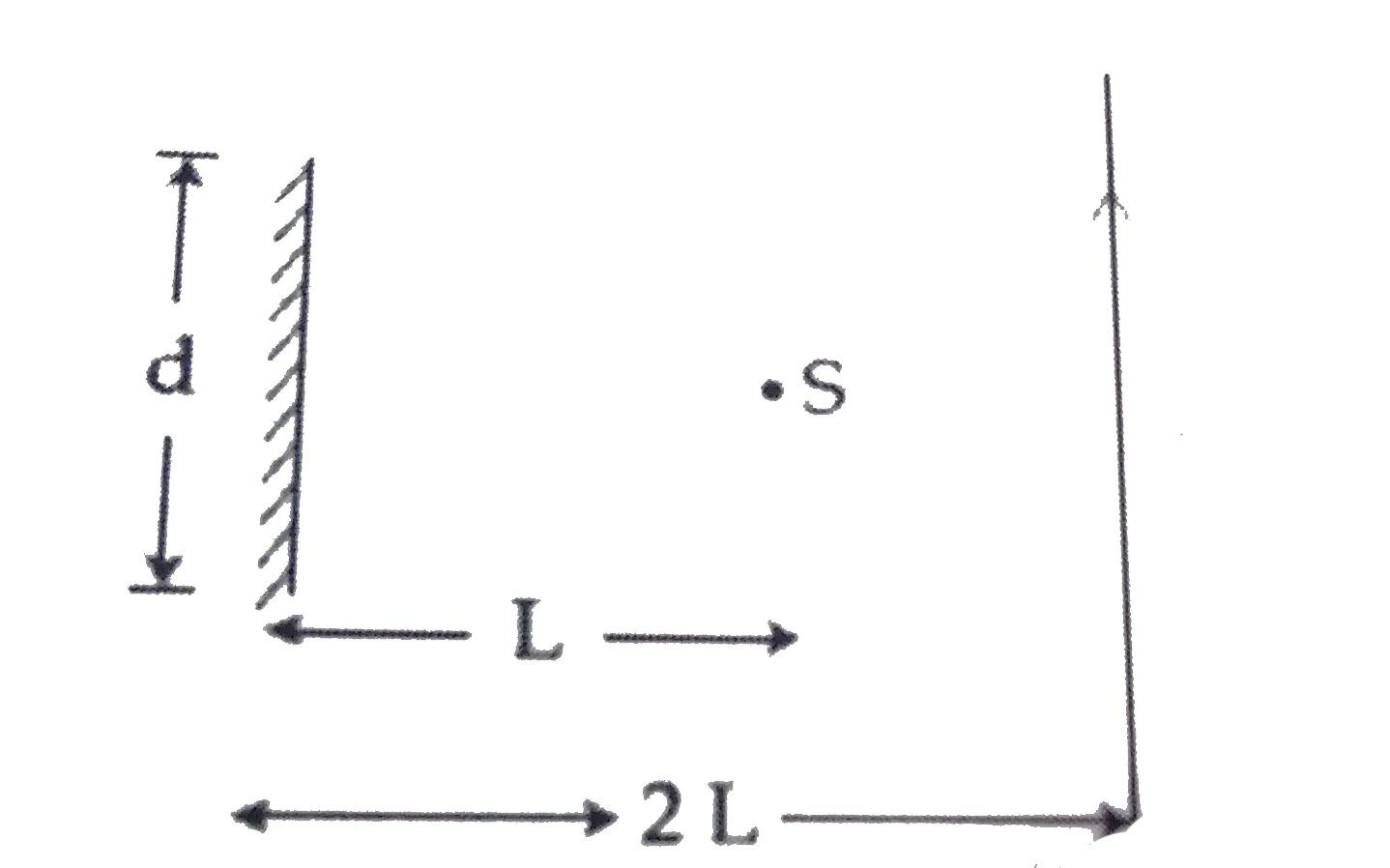
View SolutionA point source of light ,S is placed at a distance L in front of the centre of plane mirror of width d which is a hanging vertically on wall ,A man walks in front of the mirror , at a distance 2L as shown below . The distance over which the man can see the image of the light source in the mirror is :
View SolutionA caesium photocell , with a steady potential difference of 60V across , is alluminated by a bright point source of light 50cm away. When the same light is placed 1m away the photoelectrons emitted from the cell
View Solution
