A point source of light is placed at a distance of 2f from a converging lens of focal length f. The intensity onteh other side of the lens is maximum at a distance
f
between f and 2f
2f
more than 2f
The correct Answer is:C
To solve the problem step by step, we will use the lens formula and the given information about the point source of light and the converging lens.
Step 1: Identify the given values
- Focal length of the lens (f) = f
- Distance of the point source from the lens (u) = -2f (the negative sign indicates that the object is on the same side as the incoming light)
Step 2: Use the lens formula
The lens formula is given by:
1f=1v−1u
Where:
- f = focal length of the lens
- v = image distance from the lens
- u = object distance from the lens
Step 3: Substitute the known values into the lens formula
Substituting f and u into the lens formula:
1f=1v−1−2f
This simplifies to:
1f=1v+12f
Step 4: Rearrange the equation to solve for v
Rearranging the equation gives:
1v=1f−12f
Finding a common denominator (which is 2f):
1v=22f−12f=12f
Step 5: Solve for v
Taking the reciprocal of both sides:
v=2f
Step 6: Conclusion
The image is formed at a distance of 2f on the other side of the lens, which is also the point where the intensity is maximum.
Final Answer
The intensity on the other side of the lens is maximum at a distance of 2f.
---
- Focal length of the lens (f) = f
- Distance of the point source from the lens (u) = -2f (the negative sign indicates that the object is on the same side as the incoming light)
The lens formula is given by:
1f=1v−1u
Where:
- f = focal length of the lens
- v = image distance from the lens
- u = object distance from the lens
Substituting f and u into the lens formula:
1f=1v−1−2f
This simplifies to:
1f=1v+12f
Rearranging the equation gives:
1v=1f−12f
Finding a common denominator (which is 2f):
1v=22f−12f=12f
Taking the reciprocal of both sides:
v=2f
The image is formed at a distance of 2f on the other side of the lens, which is also the point where the intensity is maximum.
The intensity on the other side of the lens is maximum at a distance of 2f.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Objective -2
7 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercises
78 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer
18 Videos
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question
7 Videos
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer
11 Videos
Similar Questions
An object is placed at a distance of f2 from a convex lens of focal length f. The image will be
View SolutionA point object is placed at a distance of 12cm from a convex lens of focal length 10cm. On the other side of the lens, a convex mirror is placed at a distance of 10cm from the lens such that the image formed by the combination coincides with the object itself. The focal length of the convex mirror is
View SolutionAn object is placed at a distance f in front of a concave lens of focal length f. Locate its image.
View SolutionAn object is placed at a distance of f/2 from a convex lens. The image will be
View SolutionA luminous object is placed at a distance of 30 cm. from the convex lens of focal length 20 cm. On the other side of the lens, at what distance from the lens, a convex mirror of radius of curvature 10 cm. be placed in order to have an upright image of the object coincident with it ?
View SolutionA point source of light is kept at a distance of 15cm from a converging lens,on its optical axis.The focal length of the lens is 10cm and its diameter is 3cm ,A screen is placed on the other side of the lens ,perpendicular to the axis of lens,at a distance 20cm from it.Then find the area of the illuminated part of the screen?
View SolutionAn object is placed at a distance 24 cm in front of a convex lens of focal length 8 cm.
Calculate the distance of the image from the lens.
View SolutionA point object O is placed at a distance of 15 cm from a convex lens L of focal length 10 cm as shown in figure below. On the other side of the lens, a convex mirror M is placed such that its distance from the lens is equal to the focal length of the lens. The final image formed by this combination is observed to coincide with the object 0. Find the focal length of the convex mirror.
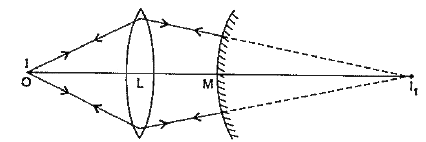
View SolutionA point source S is placed at a distance of 15 cm from a converging lens of focal length 10 cm on its principal axis. Where should a diverging miror of focal length 12 cm be placed to that a real image is formed on the source itself.
View SolutionA point object O is placed at a distance of 20cm from a convex lens of focal length 10cm as shown in the figure. At what distance x from the lens should a convex mirror of focal length 60cm, be placed so that final image coincide with the object?

View Solution
