The minimum wavelength of the X- rays produced at accelerationg potential V is λ. If the accelerating potential is changed to 2V, then the minimum wavelength would become
4λ
2λ
λ2
λ4
The correct Answer is:C
To solve the problem, we need to understand the relationship between the accelerating potential (V) and the minimum wavelength (λ) of the X-rays produced. The key concept here is that the energy of the X-rays is related to the accelerating potential.
1. Understanding the Energy Relationship:
The energy (E) of the X-rays can be expressed using the formula:
E=hcλ
where h is Planck's constant and c is the speed of light.
2. Energy Gained from Accelerating Potential:
When a charge Q is accelerated through a potential V, it gains energy given by:
E=QV
3. Setting the Energies Equal:
Since the energy gained by the charge is equal to the energy of the X-rays, we can set the two expressions for energy equal to each other:
hcλ=QV
4. Finding the Minimum Wavelength:
Rearranging the equation gives us the expression for the minimum wavelength:
λ=hcQV
5. Changing the Accelerating Potential:
Now, if we change the accelerating potential from V to 2V, we need to find the new minimum wavelength λ2:
λ2=hcQ(2V)=hc2QV
6. Relating the New Wavelength to the Old Wavelength:
We can express λ2 in terms of λ:
λ2=12(hcQV)=λ2
7. Final Result:
Therefore, when the accelerating potential is changed to 2V, the minimum wavelength becomes:
λ2=λ2
Conclusion:
The minimum wavelength of the X-rays produced at an accelerating potential of 2V is λ2.
The energy (E) of the X-rays can be expressed using the formula:
E=hcλ
where h is Planck's constant and c is the speed of light.
When a charge Q is accelerated through a potential V, it gains energy given by:
E=QV
Since the energy gained by the charge is equal to the energy of the X-rays, we can set the two expressions for energy equal to each other:
hcλ=QV
Rearranging the equation gives us the expression for the minimum wavelength:
λ=hcQV
Now, if we change the accelerating potential from V to 2V, we need to find the new minimum wavelength λ2:
λ2=hcQ(2V)=hc2QV
We can express λ2 in terms of λ:
λ2=12(hcQV)=λ2
Therefore, when the accelerating potential is changed to 2V, the minimum wavelength becomes:
λ2=λ2
The minimum wavelength of the X-rays produced at an accelerating potential of 2V is λ2.
Similar Questions
Knowledge Check
The de Broglie wavelength λ of an electron accelerated through a potential V in volts is
A1.227√VnmB0.1227√VnmC0.01227√VnmD12.27√Vnm
The de - Broglie wavelength of a particle accelerated with 150vo potential is 10−10m. If it is accelerated by 600vo, its wavelength will be
View SolutionTwo paricles have idential charges. If they are accelerated throgh identical potential differences, then the ratio of their deBrogile wavelength would be
View SolutionDe Broglie wavelength associated with an electron acclerated through a potential difference V is λ. What will be its wavelength when the accelerating potential is increased to 4V?
View SolutionThe ratio of de broglie wavelength of electron accelerated through potentials V1 and V2 is 1:2 the ratio of potentials V1:V2 is
View SolutionThe operating potential in an x-ray tube is increased by 2%. The percentage change in the cut off wavelength is
View SolutionIf the potential difference V applied to the coolidge tube is doubled, then the cut off wavelength
View SolutionThe intensity of X-rays form a Coolidge tube is plotted against wavelength λ as shown in the figure. The minimum wavelength found is λc and the wavelength of the Kα line is λk. As the accelerating voltage is increased
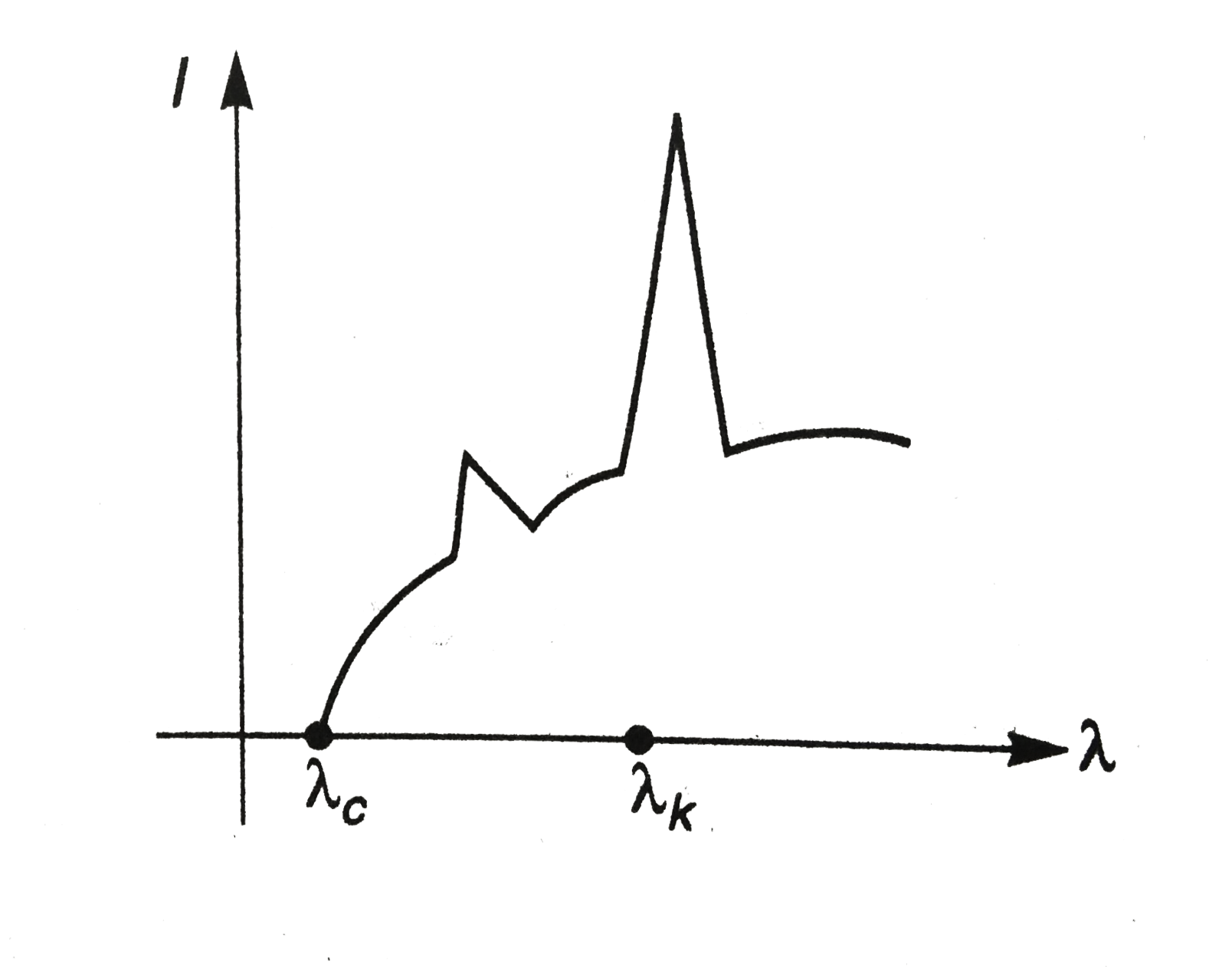
(a) λk−λc increases (b) λk−λc decreases
(c ) λk increases (d) λk decreases
View Solution