Activation energy (Ea) and rate constants (k1andk2) of a chemical reaction at two different temperature (T1andT2) are related by
In k2k1=−EaR(1T1−1T2)
In k2k1=−EaR(1T2−1T1)
In k2k1=−EaR(1T2+1T1)
In k2k1=EaR(1T1−1T2)
The correct Answer is:B, D
To solve the problem of how activation energy Ea and rate constants k1 and k2 of a chemical reaction at two different temperatures T1 and T2 are related, we can use the Arrhenius equation. Here’s a step-by-step breakdown of the solution:
Step 1: Write the Arrhenius Equation
The Arrhenius equation relates the rate constant k to the activation energy Ea, the pre-exponential factor A, the gas constant R, and the temperature T:
k=Ae−EaRT
Step 2: Write the Equation for Two Different Temperatures
For the two different temperatures T1 and T2, we can express the rate constants k1 and k2 as:
k1=Ae−EaRT1
k2=Ae−EaRT2
Step 3: Take the Natural Logarithm of Both Equations
Taking the natural logarithm of both sides for each equation gives us:
lnk1=lnA−EaRT1(1)
lnk2=lnA−EaRT2(2)
Step 4: Subtract the Two Equations
Now, we can subtract equation (1) from equation (2):
lnk2−lnk1=(−EaRT2)−(−EaRT1)
This simplifies to:
lnk2−lnk1=−EaR(1T2−1T1)
Step 5: Rewrite the Equation
We can rewrite the left side using the properties of logarithms:
ln(k2k1)=−EaR(1T2−1T1)
Step 6: Final Form
Thus, the relationship between the activation energy, rate constants, and temperatures can be expressed as:
ln(k2k1)=−EaR(1T2−1T1)
Conclusion
This equation shows how the rate constants at two different temperatures are related to the activation energy of the reaction.
The Arrhenius equation relates the rate constant k to the activation energy Ea, the pre-exponential factor A, the gas constant R, and the temperature T:
k=Ae−EaRT
For the two different temperatures T1 and T2, we can express the rate constants k1 and k2 as:
k1=Ae−EaRT1
k2=Ae−EaRT2
Taking the natural logarithm of both sides for each equation gives us:
lnk1=lnA−EaRT1(1)
lnk2=lnA−EaRT2(2)
Now, we can subtract equation (1) from equation (2):
lnk2−lnk1=(−EaRT2)−(−EaRT1)
This simplifies to:
lnk2−lnk1=−EaR(1T2−1T1)
We can rewrite the left side using the properties of logarithms:
ln(k2k1)=−EaR(1T2−1T1)
Thus, the relationship between the activation energy, rate constants, and temperatures can be expressed as:
ln(k2k1)=−EaR(1T2−1T1)
This equation shows how the rate constants at two different temperatures are related to the activation energy of the reaction.
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - ASSIGNMENT (SECTION D : Assertion - Reason Type Questions)
15 Videos
- CHEMICAL KINETICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - ASSIGNMENT (SECTION B : Objective Type Questions)
20 Videos
- CHEMICAL BONDING AND MOLECULAR STRUCTURE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CHEMICAL BONDING AND MOLECULAR STRUCTURE EXERCISE - Assignment Section J (Aakash Challengers Questions)
10 Videos
- CHEMISTRY IN EVERYDAY LIFE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CHEMISTRY IN EVERYDAY LIFE EXERCISE - Assignment ( SECTION - A)
45 Videos
Similar Questions
Activation energy (Ea) and rate constants (k1 and k2) of a chemical reaction at two different temperatures (T1 and T2) are related by
View SolutionA colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy Ea Large the value of activation energy, smaller the value of rate constant k. Larger is the value of activation energy, greater is the effect of temperature rise on rate constant k.
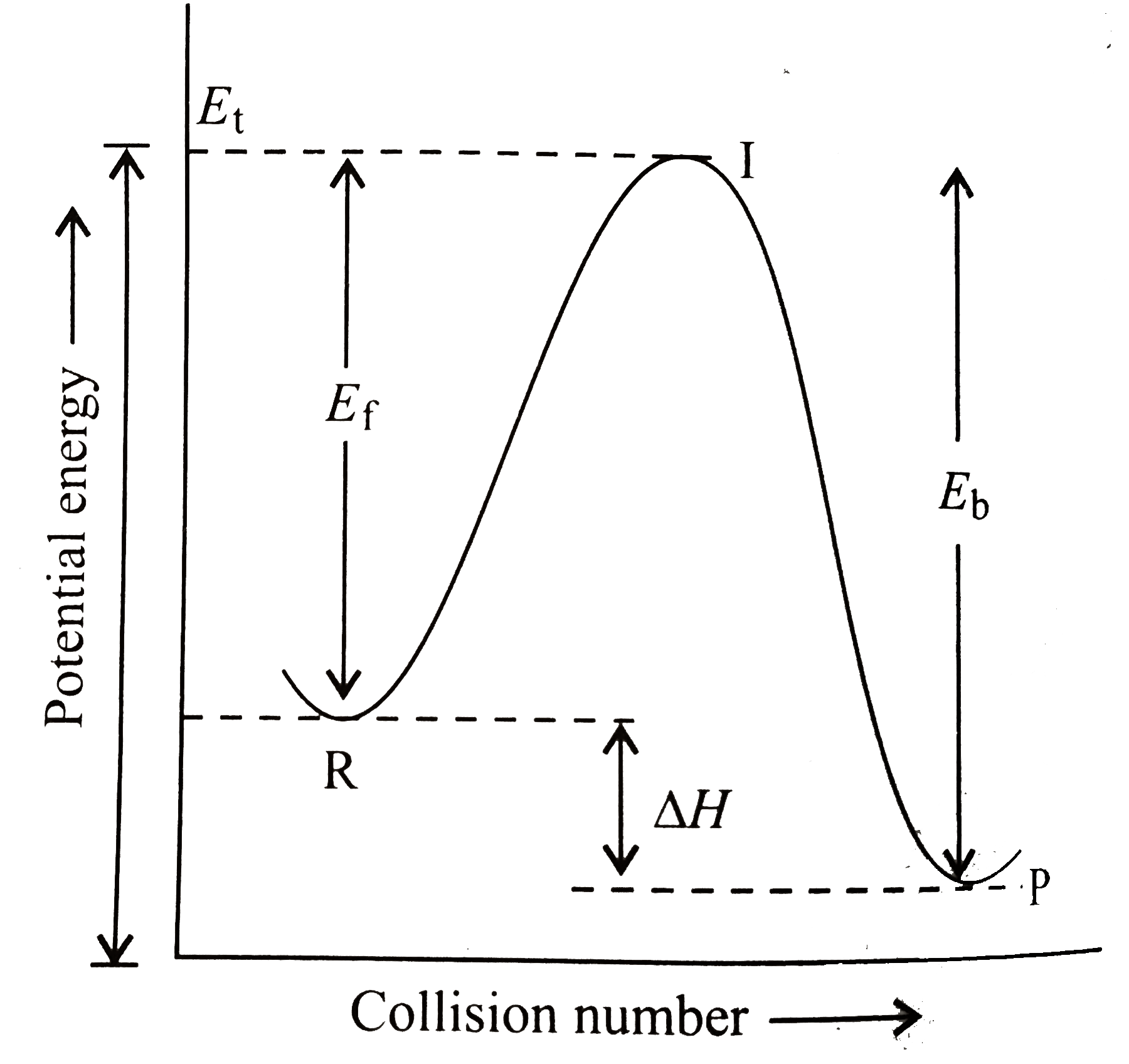
Ef= Activation energy of forward reaction
Eb= Activation energy of backward reaction
ΔH=Ef−Eb
Ef= threshold energy
For two reactions, activation energies are Ea1 and Ea2, rate constant are k1 and k2 at the same temperature. If k1>k2, then
View Solution
Knowledge Check
For a given exothermic reaction ,KPandKp' are the equilibrium constant at temperature T1andT2 respectively .Assuming that heat of reaction is constant in temperature range between T1andT2 , it is readly observed that
AKp>KpBKp<KpCKp=KpDKp=1Kp'
Consider two rods of same length and different specific heats (S1 and S2), conductivities K1 and K2 and area of cross section (A1 and A2) and both having temperature T1 and T2 at their ends. If the rate of heat loss due to conduction is equal then
View Solutionx1andx2 are susceptibility of a Paramagnetic material at temperatures T1,KandT2K respectively, then
View SolutionVariation of equilibrium constan K with temperature is given by van't Hoff equation
InK=ΔrS∘R−ΔrH∘RT
for this equation, (ΔrH∘) can be evaluated if equilibrium constants K1 and K2 at two temperature T1 and T2 are known.
log(K2K1)=ΔrH∘2.303R[1T1−1T2]
For an isomerization X(g)⇔Y(g) the temperature dependency of equilibrium constant is given by :
lnK=2−1000T
The value of ΔrS∘ at 300K is :
View SolutionTwo reaction : X→ Products and Y→ Products have rate constants k1 and k2 at temperature T and activation energies E1 and E2, respectively. If k1>k2 and E1<E2 (assuming that the Arrhenius factor is same for both the Products), then
(I) On increaisng the temperature, increase in k2 will be greater than increaisng in k1.
(II) On increaisng the temperature, increase in k1 will be greater than increase in k2.
(III) At higher temperature, k1 will be closer to k2.
(IV) At lower temperature, k1<k2
View SolutionA reactant (A) forms two products
Ak1−−→B, Activation energy Ea1
Ak2−−→C, Activation energy Ea2
If Ea2=2Ea1 then k1 and k2 are related as
View SolutionA reactant (A) forms two products
Ak1−−→B, Activation energy Ea1
Ak2−−→C, Activation energy Ea2
If Ea2=2Ea1 then k1 and k2 are related as
View SolutionThe rate constant , the activation energy and Arrhenius parameter of a chemical reaction at 25∘C are x, 10x kJ/ mol and 2xs−1 . Value of rate constant as T→∞ is
View Solution
