x1andx2 are susceptibility of a Paramagnetic material at temperatures T1,KandT2K respectively, then
x1T1=x2T2
x1T2=x2T1
x1T2=x2T1
x1√T1=x2√T1
The correct Answer is:B
To solve the problem regarding the susceptibility of a paramagnetic material at different temperatures, we can follow these steps:
Step 1: Understand the relationship between susceptibility and temperature
According to Curie's law of paramagnetism, the magnetic susceptibility (χ) of a paramagnetic material is inversely proportional to its absolute temperature (T). This can be expressed mathematically as:
χ∝1T
Step 2: Express the relationship for two different temperatures
Let χ₁ be the susceptibility at temperature T₁ and χ₂ be the susceptibility at temperature T₂. From the relationship established in Step 1, we can write:
χ1=CT1
χ2=CT2
where C is a constant for the material.
Step 3: Set up the ratio of susceptibilities
From the expressions for χ₁ and χ₂, we can set up the following ratio:
χ1χ2=T2T1
Step 4: Rearranging the ratio
Rearranging the above equation gives us:
χ1T1=χ2T2
Step 5: Conclusion
Thus, we have derived the relationship:
χ1T1=χ2T2
This means that the product of susceptibility and temperature remains constant for a paramagnetic material.
Final Answer
The correct relationship is:
χ1T1=χ2T2
According to Curie's law of paramagnetism, the magnetic susceptibility (χ) of a paramagnetic material is inversely proportional to its absolute temperature (T). This can be expressed mathematically as:
χ∝1T
Let χ₁ be the susceptibility at temperature T₁ and χ₂ be the susceptibility at temperature T₂. From the relationship established in Step 1, we can write:
χ1=CT1
χ2=CT2
where C is a constant for the material.
From the expressions for χ₁ and χ₂, we can set up the following ratio:
χ1χ2=T2T1
Rearranging the above equation gives us:
χ1T1=χ2T2
Thus, we have derived the relationship:
χ1T1=χ2T2
This means that the product of susceptibility and temperature remains constant for a paramagnetic material.
The correct relationship is:
χ1T1=χ2T2
Similar Questions
How does the magnetic susceptibility of a paramagnetic material change with temperature?
View SolutionThe velocities of sound in an ideal gas at temperature T1andT2 K are found to be V1andV2 respectively. If ther.m.s velocities of the molecules of the same gas at the same temperatures T1andT2 are v1andv2 respectively then
View Solution
Knowledge Check
For a given exothermic reaction ,KPandKp' are the equilibrium constant at temperature T1andT2 respectively .Assuming that heat of reaction is constant in temperature range between T1andT2 , it is readly observed that
AKp>KpBKp<KpCKp=KpDKp=1Kp'The correct M-H curve for a paramagnetic material at a constant temperature (T) is represented by
A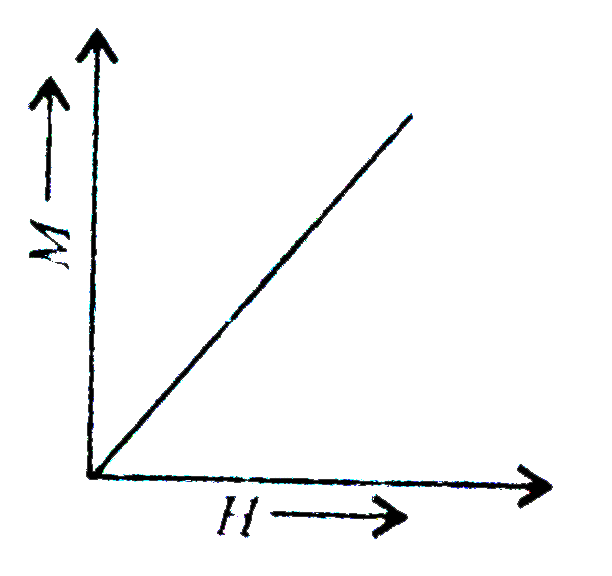 B
B C
C D
D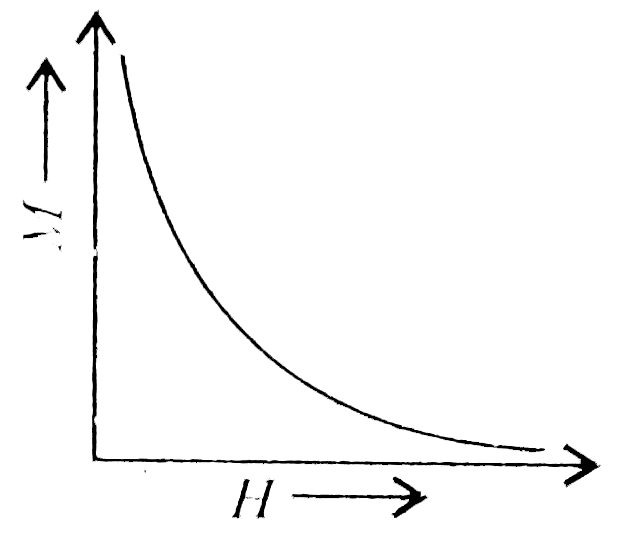
The velocities of sound in an ideal gas at temperature T1andT2 K are found to be V1andV2 respectively. If ther.m.s velocities of the molecules of the same gas at the same temperatures T1andT2 are v1andv2 respectively then
View SolutionActivation energy (Ea) and rate constants (k1 and k2) of a chemical reaction at two different temperatures (T1 and T2) are related by
View SolutionFour thin identical rods AB,AC,BD and EF made of the same material are joined as shown. The free-ends C,D and F are maintained at temperature T1,T2 and T3 respectively. Assuming that there is no loss of heat of the surroundings, the temperature at joint E when the steady state is attained is 1K(2T1+2T2+3T3). Find K(E is mid point of AB)
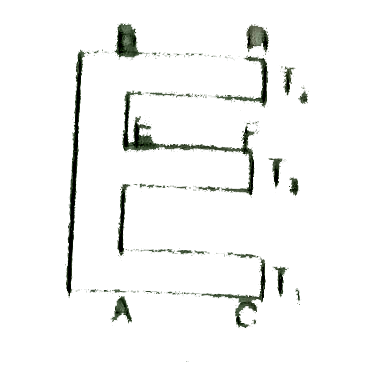
View SolutionIf K1 is the equilibrium constant at temperature T1andK2 is the equilibrium constant at temperature T2and If T2>T1 and reaction is endothermic then
View SolutionTwo conducting cylinders of equal length but different radii are connected in series between two heat baths kept at temperatures T1=300KandT2=100K, as shown in the figure. The radius of the bigger cylinder is twice that of the smaller one and the thermal conductivities of the materials of the smaller and the larger cylinders are K1andK2 respectively. If the temperature at the junction of the two cylinders in the steady state is 200 K, then K1/K2=__________.
View SolutionAssertion (A): χ−T graph for a diamagnetic material is a straight line parallel to T−axis
Reason (R ): This is because susceptibility of a diamagnetic material is not affected by temperature
View Solution
