A unifrom rope of length L and mass m1 hangs vertically from a rigid support. A block of mass m1 is attched to the free end of the rope. A transverse pulse of wavelength λ1 is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is λ2theratioλ2/λ1 ia
√m1+m2m1
√m1m2
√m1+m2m2
√m2m1
The correct Answer is:C
Step by step video & image solution for A unifrom rope of length L and mass m_(1) hangs vertically from a rigid support. A block of mass m_(1) is attched to the free end of the rope. A transverse pulse of wavelength lambda_(1) is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is lambda _(2) the ratio lambda_(2)//lambda_(1) ia by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-B ( Objective type Questions ))
45 Videos
- WAVE OPTICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assignment (Section-J (Aakash Challengers question))
1 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - D)
13 Videos
Similar Questions
A uniform rope of elngth l and mass m hangs vertically from a rigid support. A block of mass m is attached to the free end of the rope. A transverse pulse of wavelength λ is produced at the lower end of the rope. The wavelength of the pulse, when it reaches the top of the rope. is aλ. Find a2
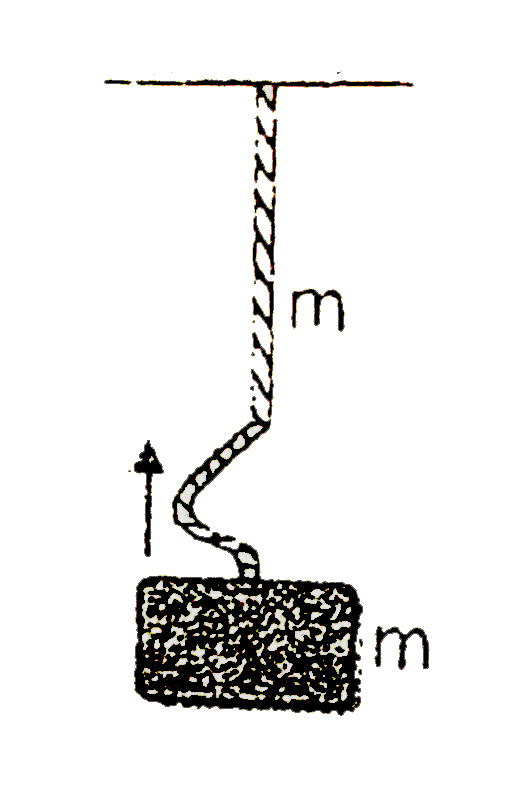
View SolutionA uniform rope of legnth L and mass m1 hangs vertically from a rigid support. A block of mass m2 is attached to the free end of the rope. A transverse pulse of wavelength λ1 is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is λ2. The ratio λ2λ1 is
View Solution
Knowledge Check
A uniform rope of length 12 mm and mass 6 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced at the lower end of the rope. What is the wavelength of the pulse when it reaches the top of the rope?
A0.06 mB0.03 mC0.12 mD0.09 m
A uniform rope of length 12 mm and mass 6 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced at the lower end of the rope. What is the wavelength of the pulse when it reaches the top of the rope?
View SolutionA uniform rope of length 12 mm and mass 6 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced at the lower end of the rope. What is the wavelength of the pulse when it reaches the top of the rope?
View SolutionA uniform rope of length 10 cm and mass 4 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced at the lower end of the rope, what is the wavelength of the pulse when it reaches the top of the rope?
View SolutionA thick uniform rope of length L is hanging from a rigid support. A transverse wave of wavelength λ0 is set up in the middle of the rope. The wavelength of the wave as it reaches the top most point is
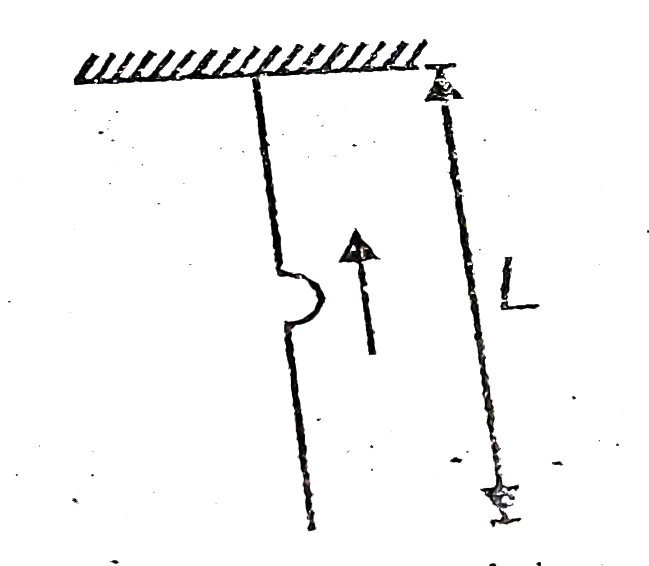
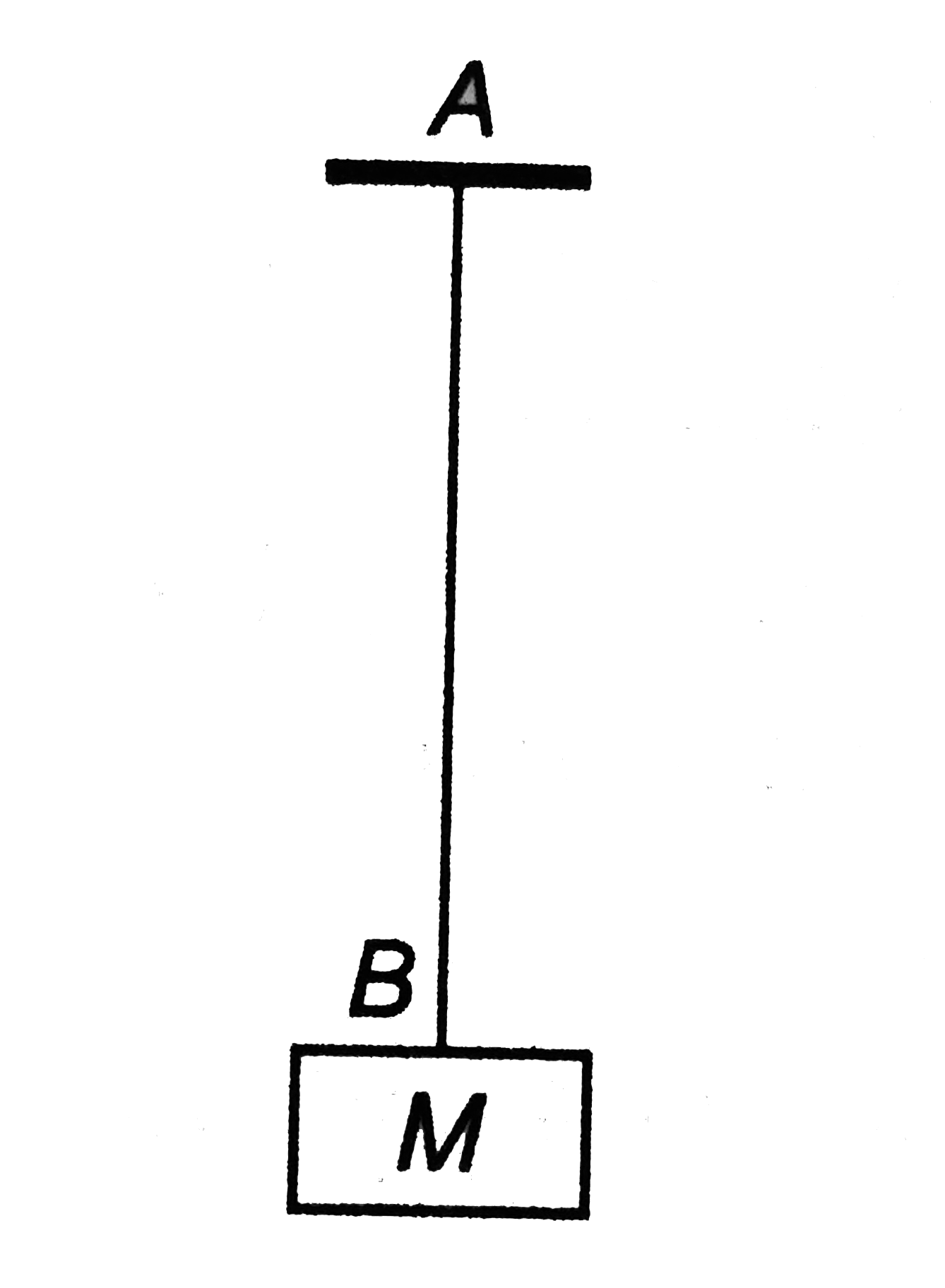
View SolutionA block of mass M=2kg is suspended from a string AB of mass 6kg as shown in figure. A transverse wave pulse of wavelength λ0 is produced at point B. find its wavelength while reaching at point A.
View SolutionA Uniform rope having mass m hags vertically from a rigid support. A transverse wave pulse is produced at the lower end. The speed v of wave pulse varies with height h from the lower end as
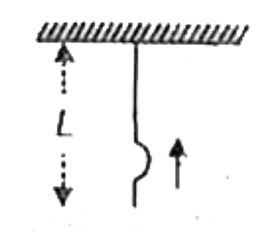
View SolutionA pulse is generated at lower end to a hanging rope of uniform density and length L. The speed of the pulse when it reaches the mid point of rope is
View Solution
