(a) Find the equivalent resistance between A and B of the network extending off to the infinity shown in the figure .

(b) If E=12V,R1=1ΩandR2=4Ω. Find the current in R2 nearest of the battery .
(a) Let the equivalent resistance of the given infinite ladder is R. Since the network extends to infinity , the resistance of the network to the right of the points C and D is also equal to R . Hence

or R=2R1+RR2R+R2=2R1R2+2R1R1+R2RR+R2
or R2+R2R=2R1R2+2R1R+R2R
or R2−2R1R−2R1R2=0
or R=2R1±√4R21+8R1R22=R1+√R21+2R1R2
(Negative resistance is not acceptable )
(b) Where R1=1Ω,R2=4Ω, the equivalent resistance
R=R1+√R21+2R1R2=4Ω
∴ The net currents is i=12V4Ω=3A
So, the current in each of 4Ω resistor in figure (c) is i2=1.5A
That is , the current in R2 nearest to the battery is 1.5A

Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Try Yourself
34 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT(SECTION-A(OBJECTIVE TYPE QUESTIONS))
69 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMMUNICATION SYSTEMS EXERCISE - ASSIGNMENT SECTION D (Assertion-Reason)
10 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
Find the equivalent resistances between the points a and c of the network shown in figure. Each resistance is equal to r.
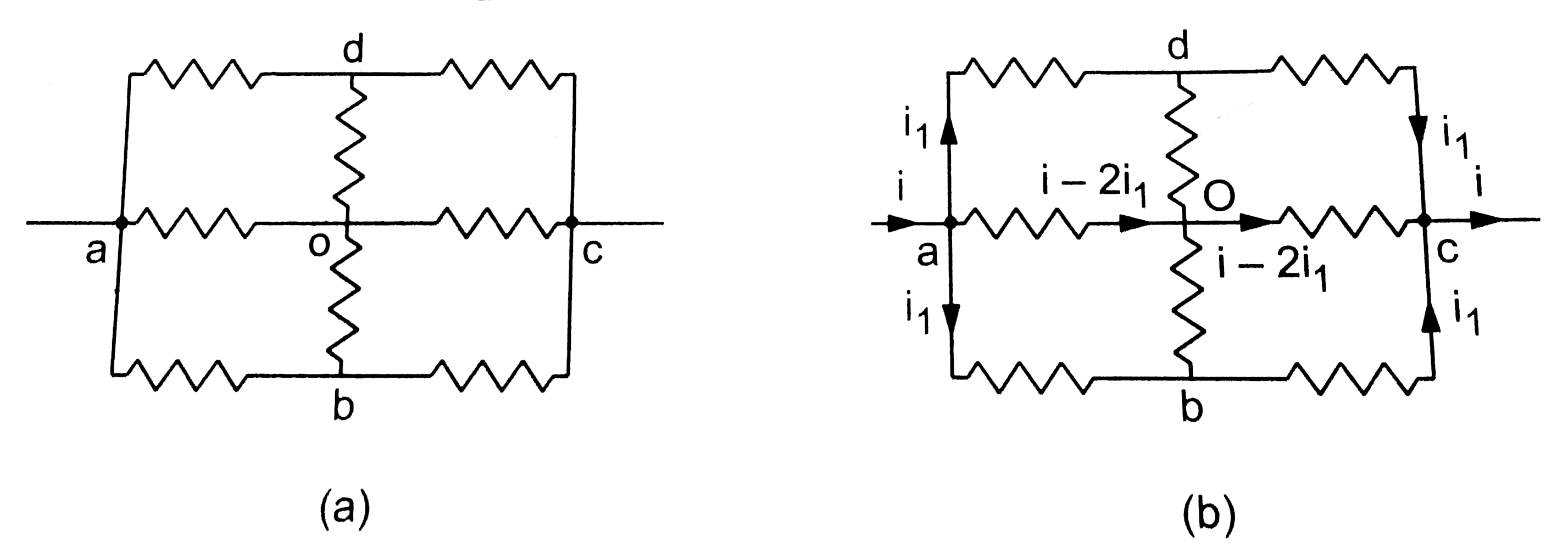
View SolutionFind the equivalent resistance of the networks shown in figure. between the points A and B.
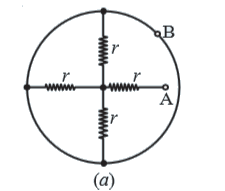
View SolutionFind the equivalent resistance of the network shown in figure between the points A and B .
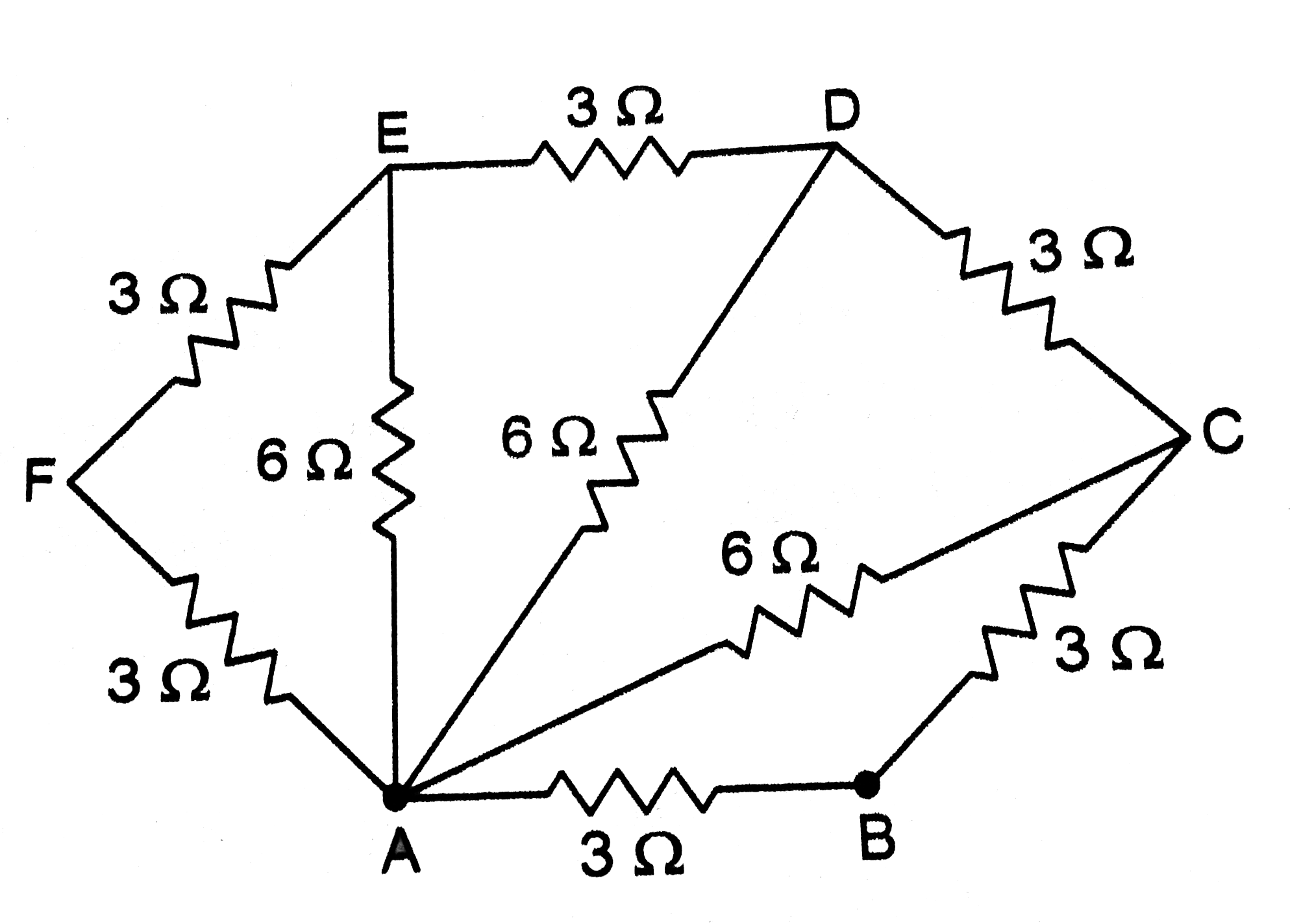
View SolutionFind the equivalent resistances of the network shown in figure between the point a and b.

View SolutionFind the equivalent resistance of the networks shown in figure between the points a and b.
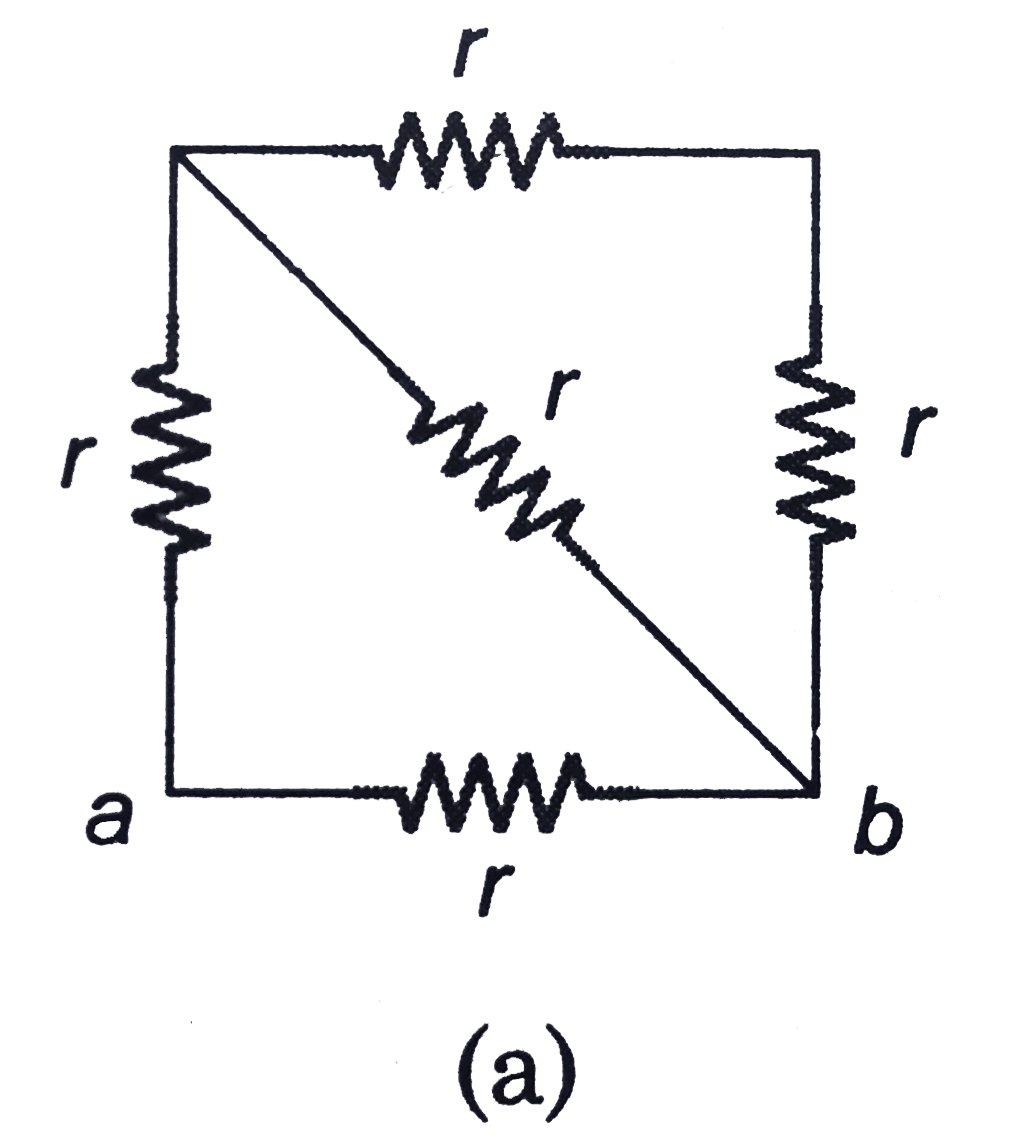
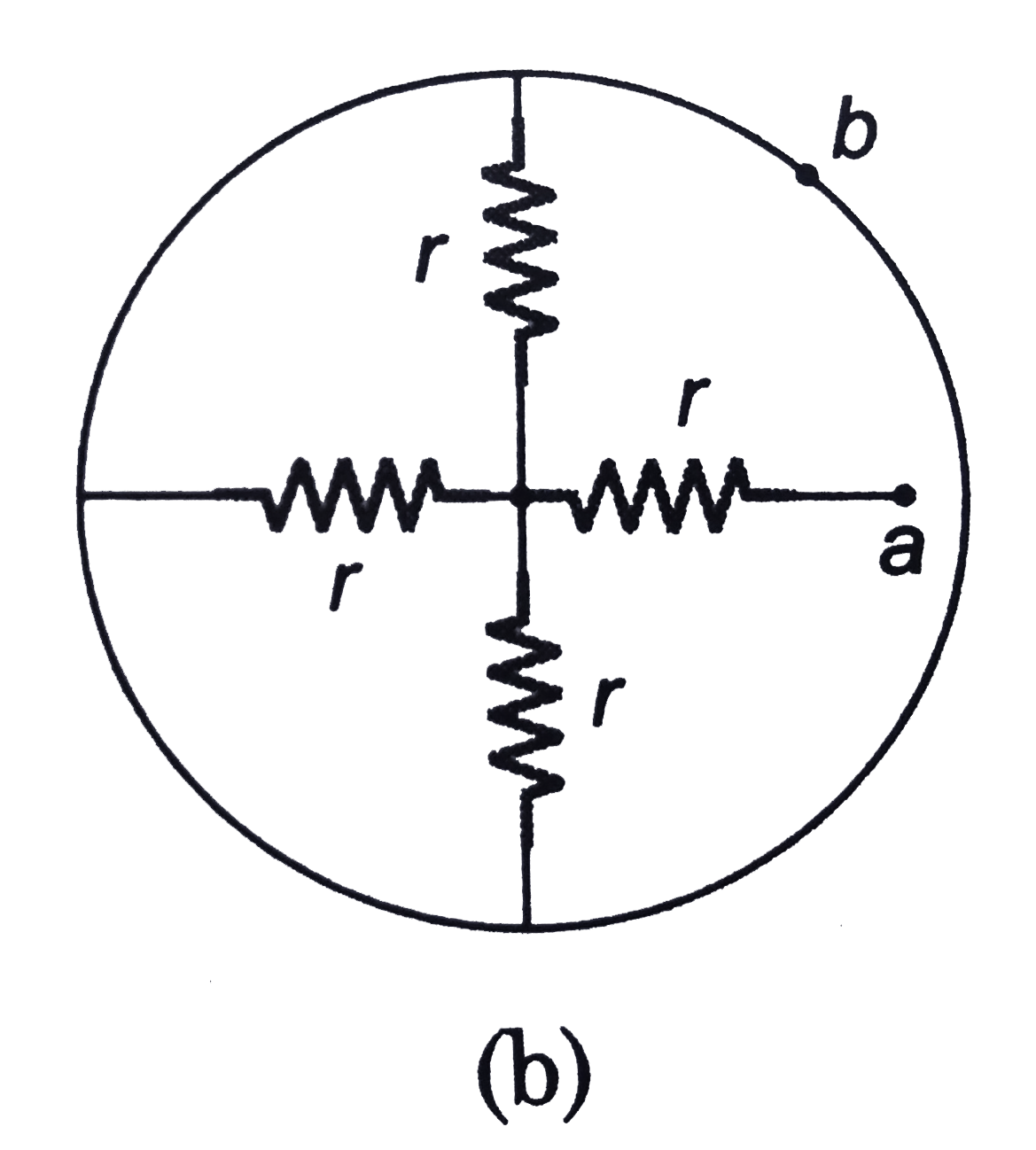
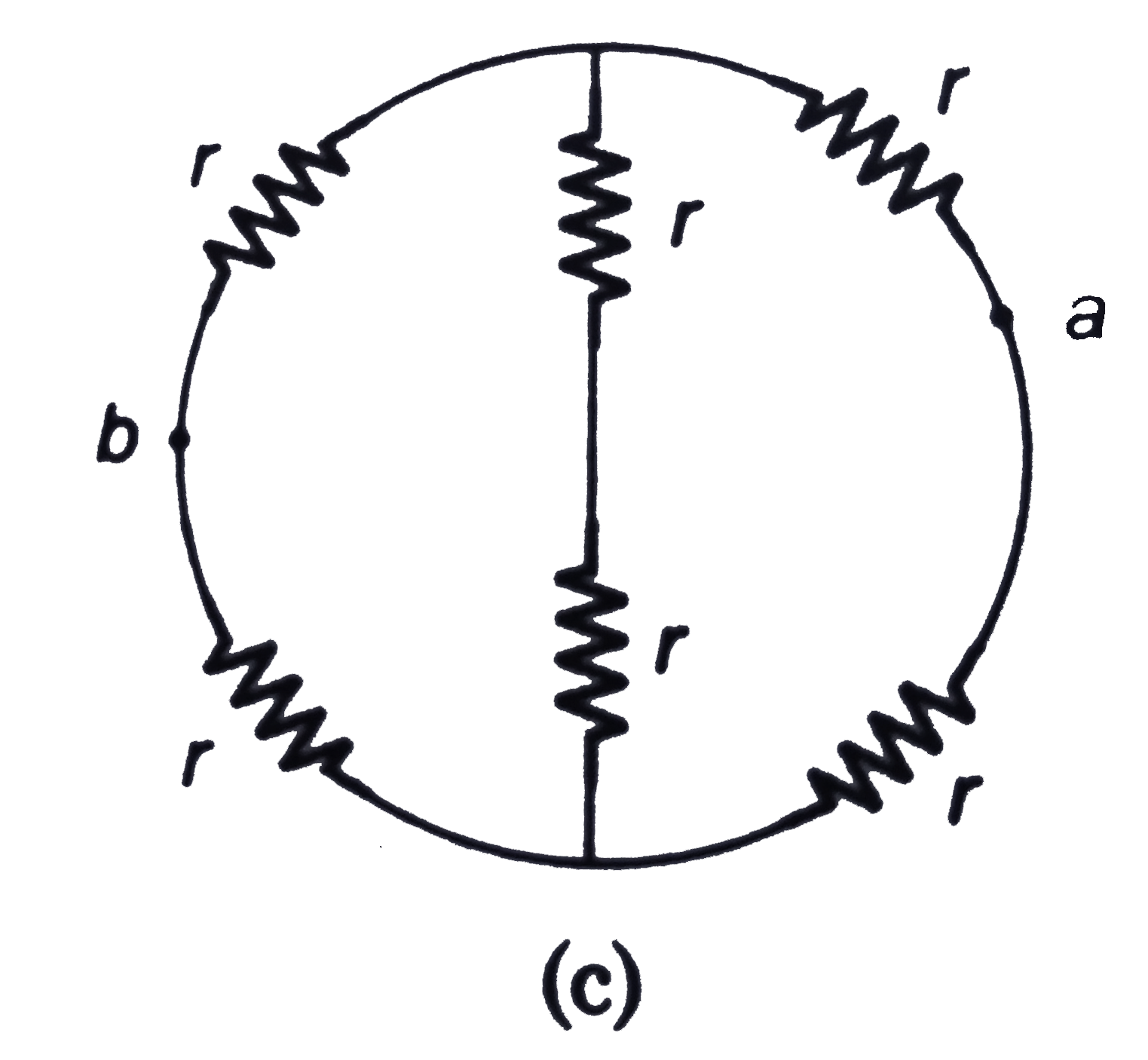
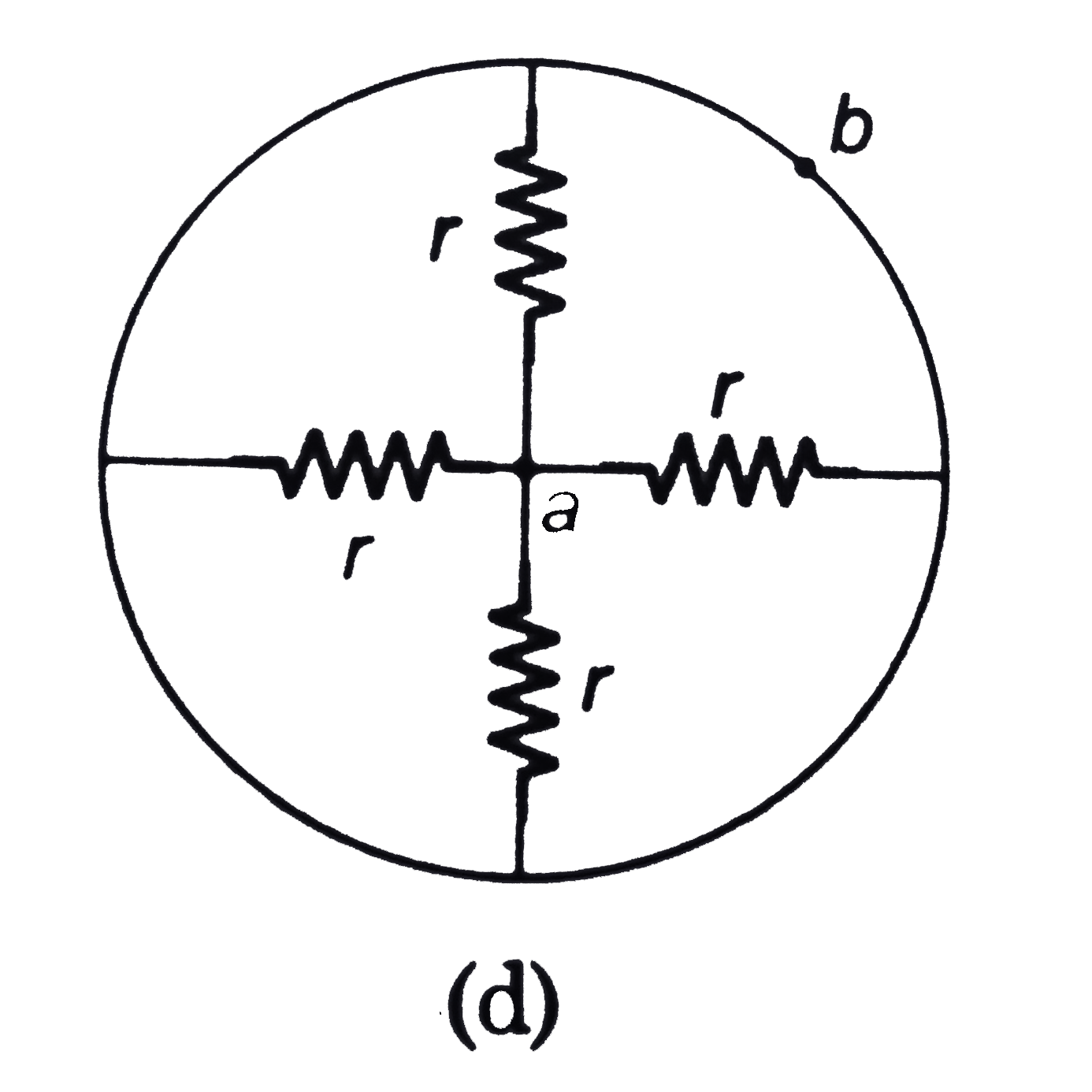
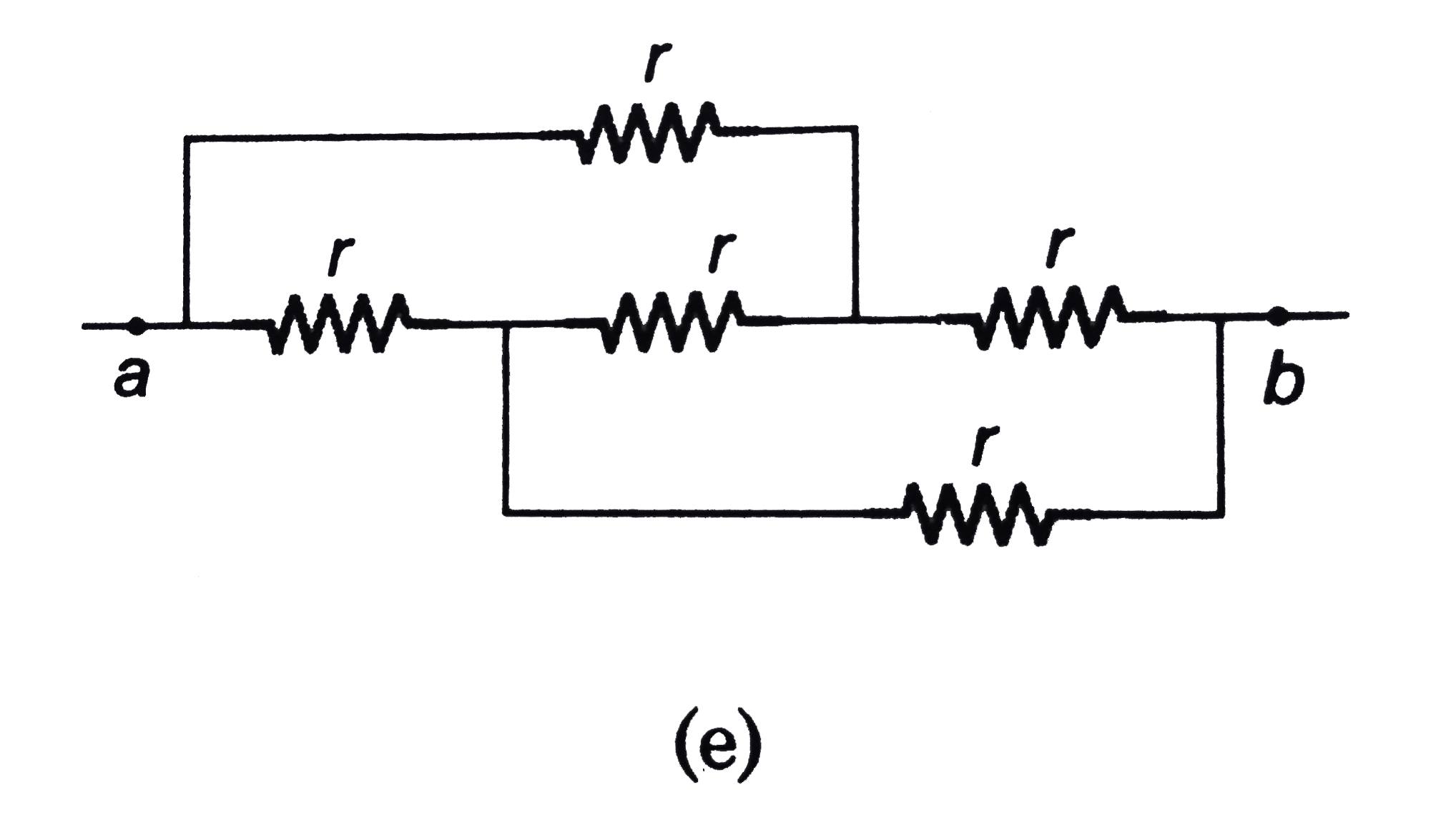
View SolutionIn the following circuit ,E1=4V,R1=2Ω,
E2=6V,R2=2Ω,andR3=4Ω. Find the currents i1andi2
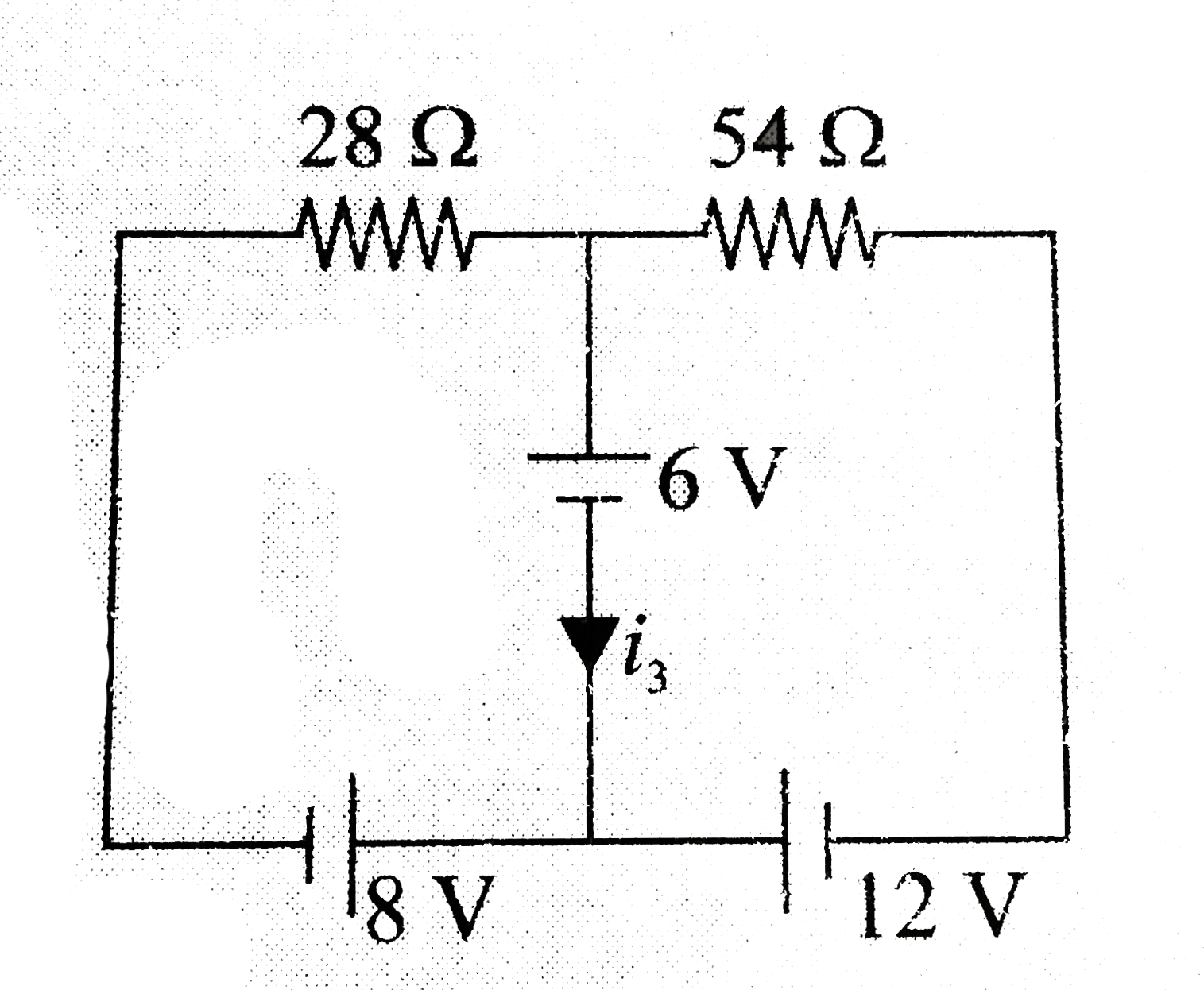
View SolutionIn the circuit shown in figure

Current through R2 is zero if R4=2Ω and R3=4Ω In this case
View SolutionIn the circuit shown below E1=4.0V,R1=2Ω,E2=6.0V,R2=4Ω and R3=2Ω. The current I1 is
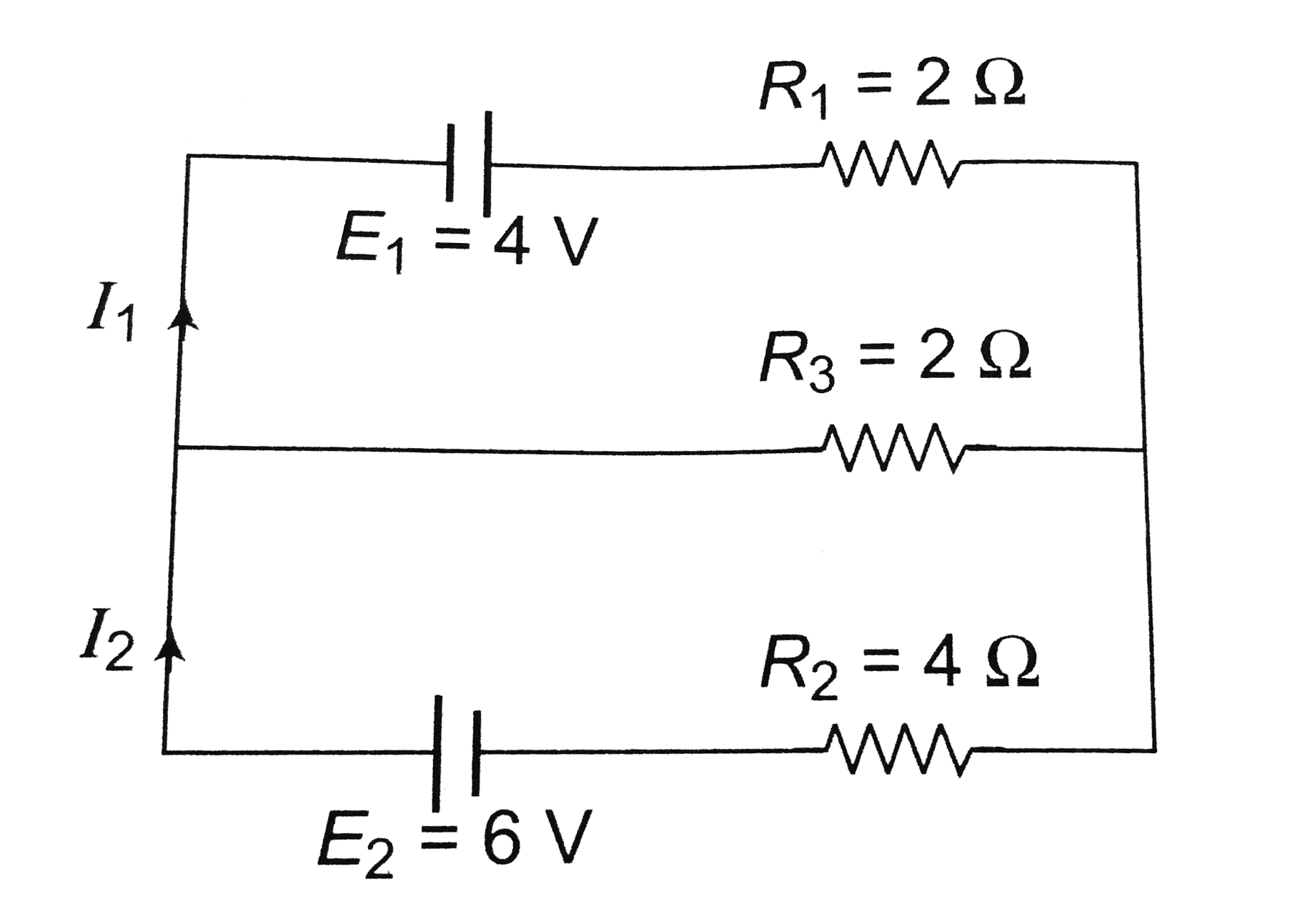
View SolutionIn the circuit shown, E1=7V,E2=7V,R1=R2=1Ω and R3=3Ω respectively. The current through the resistance R3
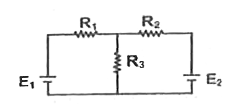
View SolutionIn the circuit shown, E1=7V,E2=7V,R1=R2=1Ω and R3=3Ω respectively. The current through the resistance R3

View Solution