Two short magnet having magnetic moment in the ratio 27:8, when placed on the opposite sides of a deflection magnetometer, produce no deflection. If the distance of the weaker magnet is 0.12m from the centre of deflection magnetometer, the distance of the stronger magnet from the centre is
0.06m
0.08m
0.12m
0.18m
The correct Answer is:D
To solve the problem, we need to find the distance of the stronger magnet from the center of the deflection magnetometer, given the magnetic moments of the two magnets and the distance of the weaker magnet.
1. Define the Magnetic Moments:
Let the magnetic moment of the stronger magnet be M1 and that of the weaker magnet be M2. According to the problem, the ratio of their magnetic moments is given as:
M1M2=278
2. Assign the Distance:
The distance of the weaker magnet from the center of the magnetometer is given as d2=0.12m. Let the distance of the stronger magnet from the center be d1 (which we need to find).
3. Magnetic Field Calculation:
The magnetic field B produced by a magnetic dipole at a distance d is given by:
B=μ04π⋅2Md3
Therefore, the magnetic field due to the stronger magnet at distance d1 is:
B1=μ04π⋅2M1d31
And for the weaker magnet at distance d2:
B2=μ04π⋅2M2d32
4. Set the Magnetic Fields Equal:
Since there is no deflection, the magnetic fields produced by both magnets must be equal:
B1=B2
This leads to:
2M1d31=2M2d32
The μ04π and 2 cancel out, simplifying to:
M1d31=M2d32
5. Substituting the Ratio of Magnetic Moments:
Substitute M1=278M2 into the equation:
278M2d31=M2(0.12)3
Cancel M2 from both sides:
278d31=1(0.12)3
6. Cross-Multiply and Solve for d31:
Cross-multiplying gives:
27⋅(0.12)3=8⋅d31
Calculate (0.12)3:
(0.12)3=0.001728
Thus:
27⋅0.001728=8⋅d31
0.046656=8d31
d31=0.0466568=0.005832
7. Taking the Cube Root:
Now, take the cube root to find d1:
d1=√(3)0.005832≈0.181
Rounding gives:
d1≈0.18m
Final Answer:
The distance of the stronger magnet from the center of the deflection magnetometer is approximately 0.18m.
---
Let the magnetic moment of the stronger magnet be M1 and that of the weaker magnet be M2. According to the problem, the ratio of their magnetic moments is given as:
M1M2=278
The distance of the weaker magnet from the center of the magnetometer is given as d2=0.12m. Let the distance of the stronger magnet from the center be d1 (which we need to find).
The magnetic field B produced by a magnetic dipole at a distance d is given by:
B=μ04π⋅2Md3
Therefore, the magnetic field due to the stronger magnet at distance d1 is:
B1=μ04π⋅2M1d31
And for the weaker magnet at distance d2:
B2=μ04π⋅2M2d32
Since there is no deflection, the magnetic fields produced by both magnets must be equal:
B1=B2
This leads to:
2M1d31=2M2d32
The μ04π and 2 cancel out, simplifying to:
M1d31=M2d32
Substitute M1=278M2 into the equation:
278M2d31=M2(0.12)3
Cancel M2 from both sides:
278d31=1(0.12)3
Cross-multiplying gives:
27⋅(0.12)3=8⋅d31
Calculate (0.12)3:
(0.12)3=0.001728
Thus:
27⋅0.001728=8⋅d31
0.046656=8d31
d31=0.0466568=0.005832
Now, take the cube root to find d1:
d1=√(3)0.005832≈0.181
Rounding gives:
d1≈0.18m
The distance of the stronger magnet from the center of the deflection magnetometer is approximately 0.18m.
Topper's Solved these Questions
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION A)
36 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION B)
24 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - Assignment Section D (Assertion- Reason Type Questions)
8 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-D) (Assertion-Reason Type Questions)
15 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - J
9 Videos
Similar Questions
Knowledge Check
A short bar magnet has a magnetic moment of 0.65TJ−1, then the magnitude and direction of the magnetic field produced by the magnet at a distance 8 cm from the centre of magnet on the axis is
A2.5×10−4T, along NS directionB2.5×10−4T, along SN directionC4.5×10−4T, along NS directionD4.5×10−4T, along NS directionA short bar magnet has a magnetic moment of 0.39 J T−1. The magnitude and direction of the magnetic field produced by the magnet at a distance of 20 cm from the centre of the magnet on the equatorial line of the magnet is
A0.049 G, N-S directionB4.95 G, S-N directionC0.0195 G, S-N directionD19.5 G, N-S direction
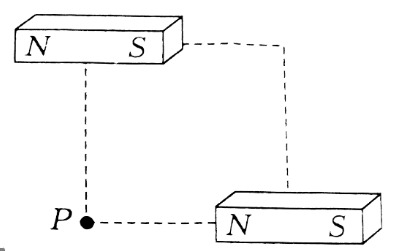
Two short magnets of magnetic moment 1000Am2 are placed as shown at the corners of a square of side 10cm. The net magnetic induction at P is
View SolutionIn tan A position two short bar magnets of magnetic moments in ratio of √3:1 are placed at same distance respectively . If the deflection produced for the first magnet be 60∘ then what will be deflection for second magnet ?
View SolutionThe needle of a deflection galvanometer shows a deflection of 60∘ due to a short bar magnet at a certain distance in tan A position. If the distance is doubled, the deflection is
View SolutionIn tan A position two short bar magnets of magnetic moments in the ratio of 1:√3 aer placed at the same distnace respectively. If the definection produced for the first magnet be 30∘, then what will be defication for the second magnet ?
View SolutionA short bar magnet has a magnetic moment of 0⋅48JT−1. Give the direction and magnitude of the magnetic field produced by the magnet at a distance of 10cm from the centre of the magnet on (i) the axis (ii) the equatorial line (normal bisector) of the magnet.
View SolutionA short bar magnet has a magnetic moment of 0⋅48JT−1. Give the direction and magnitude of the magnetic field produced by the magnet at a distance of 10cm from the centre of the magnet on (i) the axis (ii) the equatorial line (normal bisector) of the magnet.
View Solution
