A: In the expression for Lorentza force, →F=q(→v×→B+→E). If one switches to a frame with instantaneous velcoity →v
R: There exists an appropriate electric field in the new frame.
If both Assertion & Reason are true and the reason is the correct explanation of the assertion then mark (1)
If both Assertion & Reason are true but the reason is not the correct explanation of the assertion, then mark 2.
If assertion is true statement but Reason is false, then mark (3)
If both Assertion and Reason are false statements, then mark (4)
The correct Answer is:A
To solve the problem, we need to analyze the assertion and reason provided regarding the Lorentz force and the transformation of electric and magnetic fields when switching frames of reference.
1. Understanding the Lorentz Force:
The Lorentz force acting on a charge q moving with velocity →v in an electromagnetic field is given by the equation:
→F=q(→v×→B+→E)
Here, →E is the electric field, and →B is the magnetic field.
2. Switching Frames of Reference:
When we switch to a different inertial frame moving with an instantaneous velocity →v, we need to consider how the electric and magnetic fields transform. The transformation of fields is governed by the laws of electromagnetism.
3. Electric and Magnetic Field Transformation:
In the new frame, the electric field →E′ and magnetic field →B′ can be expressed in terms of the original fields →E and →B as follows:
→E′=→E+→v×→B
→B′=→B−1c2(→v×→E)
where c is the speed of light.
4. Existence of an Appropriate Electric Field:
In the new frame, the electric field →E′ includes a term that depends on the velocity →v and the magnetic field →B. This means that there exists an electric field in the new frame that accounts for the motion of the charge.
5. Conclusion:
Since both the assertion and reason are true, and the reason correctly explains the assertion, we conclude that:
- The assertion is true: The expression for the Lorentz force holds when switching to a frame with instantaneous velocity →v.
- The reason is true: There exists an appropriate electric field in the new frame due to the transformation of fields.
Final Answer:
Both the assertion and reason are true, and the reason is the correct explanation for the assertion.
---
The Lorentz force acting on a charge q moving with velocity →v in an electromagnetic field is given by the equation:
→F=q(→v×→B+→E)
Here, →E is the electric field, and →B is the magnetic field.
When we switch to a different inertial frame moving with an instantaneous velocity →v, we need to consider how the electric and magnetic fields transform. The transformation of fields is governed by the laws of electromagnetism.
In the new frame, the electric field →E′ and magnetic field →B′ can be expressed in terms of the original fields →E and →B as follows:
→E′=→E+→v×→B
→B′=→B−1c2(→v×→E)
where c is the speed of light.
In the new frame, the electric field →E′ includes a term that depends on the velocity →v and the magnetic field →B. This means that there exists an electric field in the new frame that accounts for the motion of the charge.
Since both the assertion and reason are true, and the reason correctly explains the assertion, we conclude that:
- The assertion is true: The expression for the Lorentz force holds when switching to a frame with instantaneous velocity →v.
- The reason is true: There exists an appropriate electric field in the new frame due to the transformation of fields.
Both the assertion and reason are true, and the reason is the correct explanation for the assertion.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION C47videos
MOVING CHARGE AND MAGNESIUM
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - J)2videos
MOTION IN STRAIGHT LINE
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment Section J (Aakash Challengers Questions)5videos
MOVING CHARGES AND MAGNETISM
Similar Questions
(a) Write the expression for the force, →F, acting on a charged particle of charge 'q', moving with a velocity →V in the presence of both electric field →E and magnetic field →B. Obtain the condition under which the particle moves undeflected through the fields.
(b) A rectangular loop of size l×b carrying a steady current I is placed in a uniform magnetic field →B. Prove that the torque →τ acting on the loop is given by
→τ=→m×→B, where →m is the magnetic moment of the loop.View SolutionWrite an expression in a vector form for the Lorentz magnetic force →F on a charge Q moving with velocity →V in a magnetic field →B. What is the direction of the magnetic force?
View SolutionThe rectangualr wire- frame, shown in has a width d, mass m, resistance R and a large length. A uniform magnetic field B exists to the left of the frame. A constant force F starts pushing the frame into the magnetic field at t =0. (a) Find the acceleration of the frame when its speed has increased to v. (b) Show that after some time the frame will move with a constant velocity till the whole frame enters into the magnetic field. find this velocity v0. (c) show that the velocity at tiem t is given by v=v0(1−e−Ftmv0.
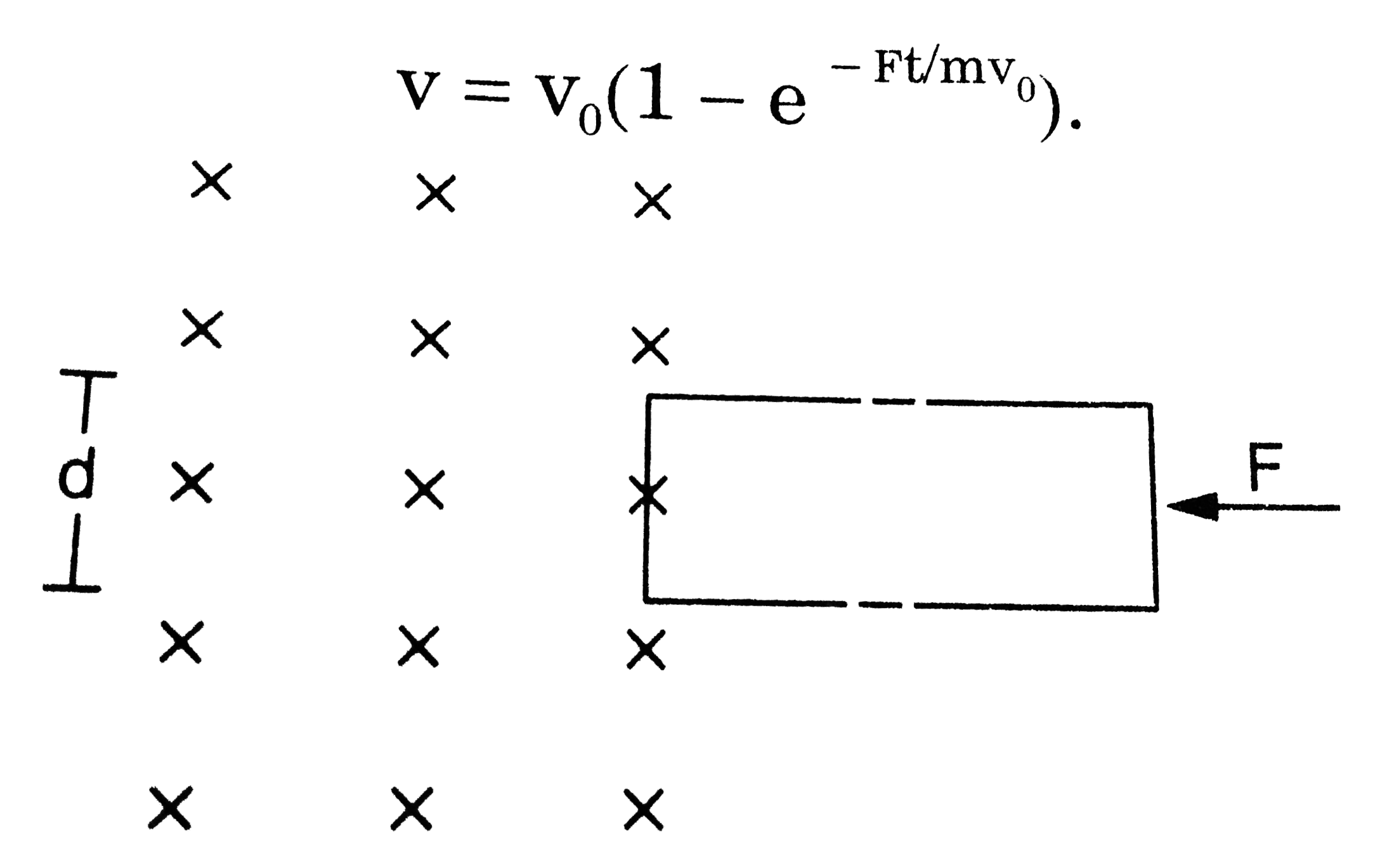 View Solution
View SolutionThe figure shows a rectangular conducting frame MNOP of resistance R placed partly in a perpendicular magnetic field →B and moved with velocity →V as shown in the figure.
Obtain the expressions for the
(a) force acting on the arm 'ON' and its direction, and
(b) power required to move the frame to get a steady emf induced between the arms MN and PO.
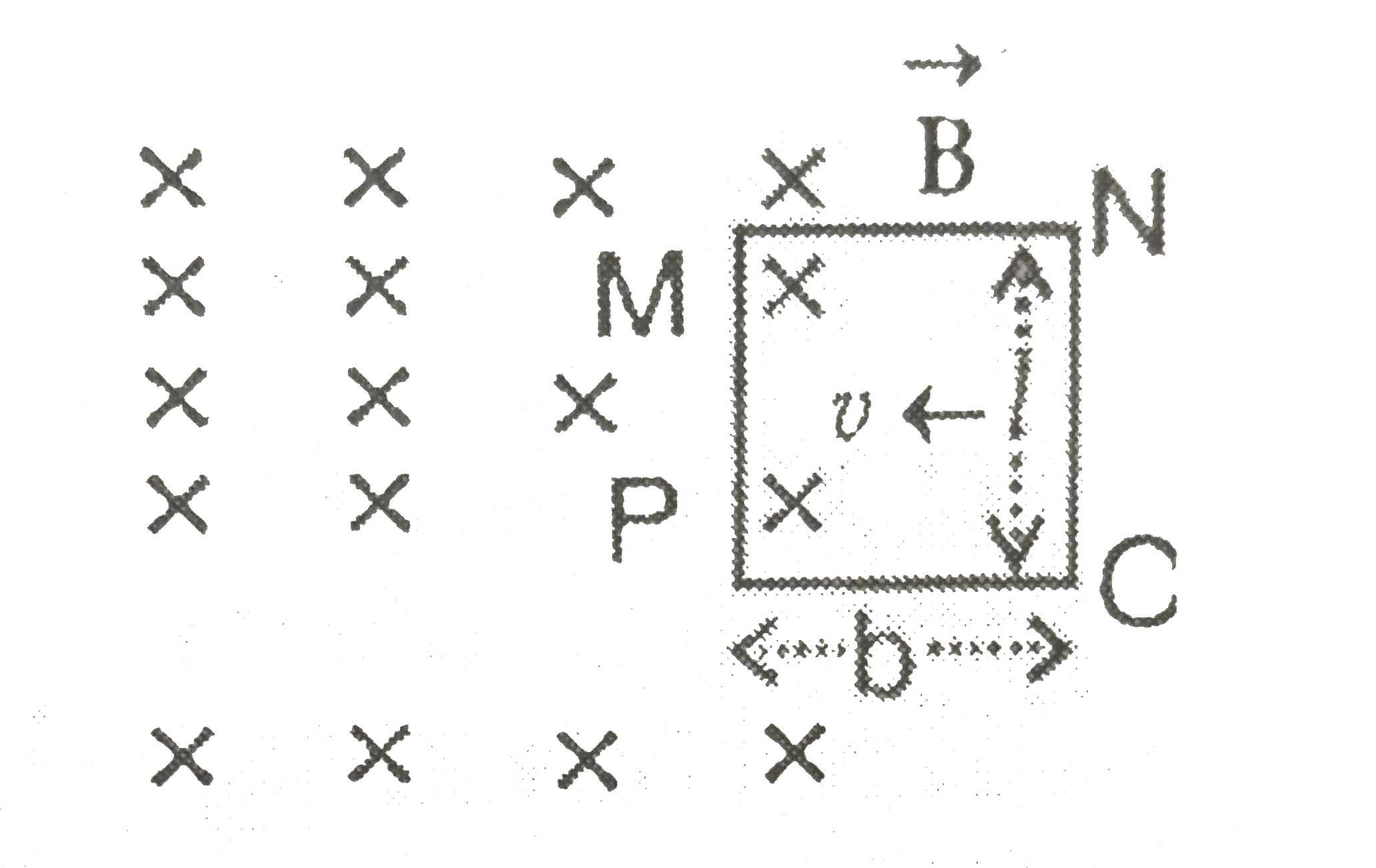 View Solution
View SolutionA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of non=inertial frame of reference. The relationship between the force →Frot experienced by a particle of mass m moving on the rotating disc and the force →F∈ experienced by the particle in an inertial frame of reference is
→Frot=→Fin+2m(→vrot×→ω)+m(→ω×→r)×→ω.
where →vrot is the velocity of the particle in the rotating frame of reference and →r is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (→ω=ωˆk). A small block of mass m is gently placed in the slot at →r(R/2)ˆi at t=0 and is constrained to move only along the slot.
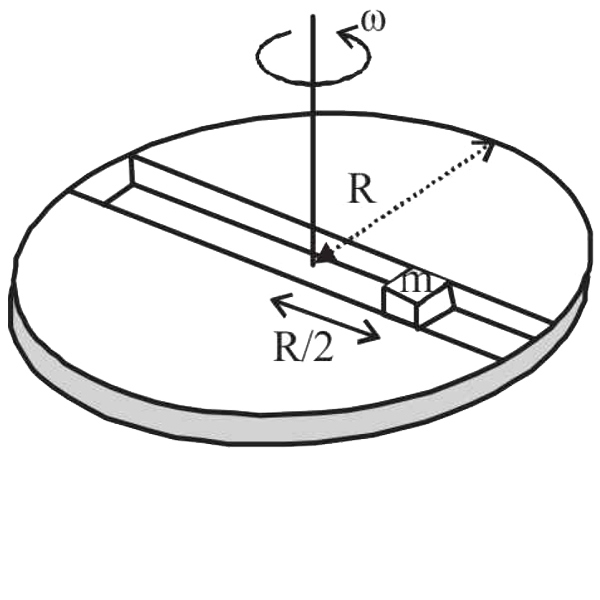
The distance r of the block at time isView SolutionA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of non=inertial frame of reference. The relationship between the force →Frot experienced by a particle of mass m moving on the rotating disc and the force →F∈ experienced by the particle in an inertial frame of reference is
→Frot=→Fin+2m(→vrot×→ω)+m(→ω×→r)×→ω.
where →vrot is the velocity of the particle in the rotating frame of reference and →r is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (→ω=ωˆk). A small block of mass m is gently placed in the slot at →r(R/2)ˆi at t=0 and is constrained to move only along the slot.
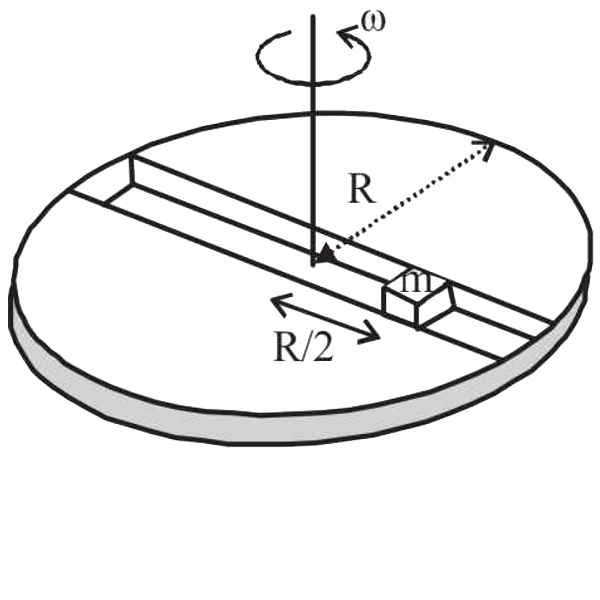
The net reaction of the disc on the block isView Solution(A)Two point charges q1 and q2 are kept r distance apart in a uniform external electric field →E. Find the amount of work done in assembling this system of charges. (B) A cube of side 20 cm is kept in a region as shown in the figure. An electric field →E exists in the region such that the potential at a point is given by V=10x+5, where V is in volt and x is in m. Find the electric field →E and (ii) total electric flux through the cube.
 View Solution
View SolutionA point charges Q is moving in a circular orbit of radius R in the x-y plane with an angular velocity ω. This can be considered as equivalent to a loop carrying a steady current Qω2π. S uniform magnetic field along the positive z-axis is now switched on, which increases at a constant rate from 0 to B in one second. Assume that the radius of hte orbit remains constant. The application of hte magnetic field induces an emf in the orbit. The induced emf is defined as the work done by an induced electric field in moving a unit positive charge around a closed loop. It si known that, for an orbiting charge, the magnetic dipole moment is proportional to the angular momentum with a porportionality constant λ.
The magnitude of the induced electric field in the orbit at any instant of time during the time interval of the mangnetic field change isView SolutionA point charges Q is moving in a circular orbit of radius R in the x-y plane with an angular velocity ω. This can be considered as equivalent to a loop carrying a steady current Qω2π. S uniform magnetic field along the positive z-axis is now switched on, which increases at a constant rate from 0 to B in one second. Assume that the radius of hte orbit remains constant. The application of hte magnetic field induces an emf in the orbit. The induced emf is defined as the work done by an induced electric field in moving a unit positive charge around a closed loop. It si known that, for an orbiting charge, the magnetic dipole moment is proportional to the angular momentum with a porportionality constant λ.
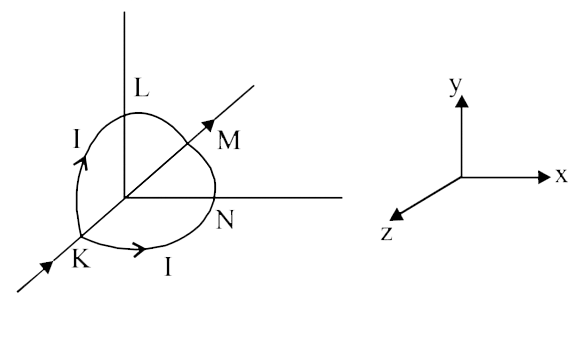
The magnitude of the induced electric field in the orbit at any instant of time during the time interval of the mangnetic field change isView SolutionA circular loop of radius R is bent along a diameter and given a shapes as shown in the figure. One of the semicircles (KNM) lies in the x−z plane with their centres and the other one (KLM) in the y−z plane with their centres at the origin. current I is flowing through each of the semi circles as shown in figure.
(a) A particle of charge q is released at the origin with a velocity →v=−v0ˆi. Find the instantaneous force →F on the particle . Assume that space is gravity free.
(b) If an external uniform magnetic field B0ˆj is applied , determine the force →F1and→F2 on the semicircles KLMandKNM due to the field and the net force →F on the loop.
 View Solution
View Solution

