A frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity $ω$ is an example of non=inertial frame of reference. The relationship between the force ${\to F}_{r o t}$ experienced by a particle of mass m moving on the rotating disc and the force ${\to F}_{\in}$ experienced by the particle in an inertial frame of reference is
${\to F}_{r o t} = {\to F}_{i n} + 2 m ({\to v}_{r o t} \times \to ω) + m (\to ω \times \to r) \times \to ω$ .
where ${\to v}_{r o t}$ is the velocity of the particle in the rotating frame of reference and $\to r$ is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed $ω$ about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis $(\to ω = ω ˆ k)$ . A small block of mass m is gently placed in the slot at $\to r (R / 2) ˆ i$ at $t = 0$ and is constrained to move only along the slot.

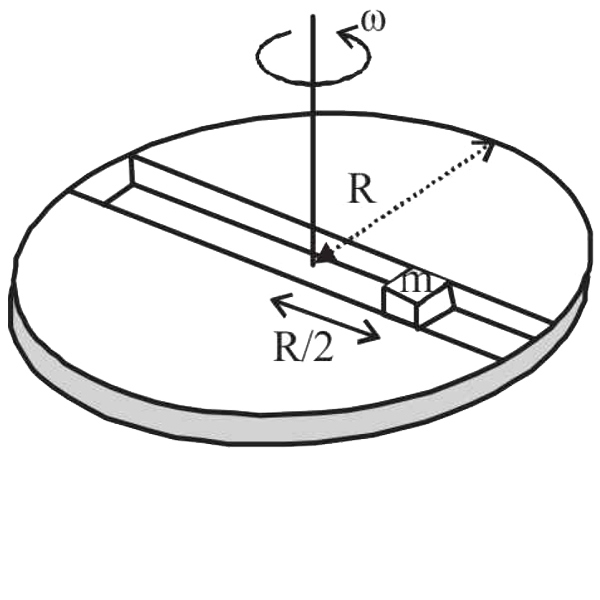
The distance r of the block at time is

A

$\frac{R}{2} cos 2 ω t$

B

$\frac{R}{2} cos ω t$

C

$\frac{R}{4} (e^{ω t} + e^{- ω t})$

D

$\frac{R}{4} (e^{2 ω t} + e^{- 2 ω t})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

In the expression ${\to F}_{e x t} = {\to F}_{\in} + 2 m (V_{r x t} \times \to ω) + m (\to ω \times \to r) \times \to ω$
The third term is radially outward i.e., this goes towards increasing ${\to V}_{r x t}$ .
2nd term is perpendicular to edge of slot and is cancelled of Normal reaction from edge of slot.
So, for radial direction.
$F = m ω^{2} r, (m d^{2} r) ({d t}^{2}) = m ω^{2} r$
i.e., $\frac{d^{2} r}{{d t}^{2}} = ω^{2} r$
Solution to this differential equation is $r = A e^{ω t} + B e^{- ω t}$
Where A and B are constants.
* for detailed solution of above differential equation see the end of this solution:
At $t = 0, r = \frac{R}{2}, \frac{R}{2} = A + B$
Also, $V_{r x t} = \frac{d r}{d t} = A ω e^{ω t} - B ω e^{- ω t}$
At t=0, $V_{r x t} = 0$ , so,
$0 = (A - B) ω, ∴ A = B - \frac{R}{4}$
So, $r = \frac{R}{4} (e^{ω t} + e^{- ω t})$
So, $r = \frac{R}{4} [e^{ω t} + e^{- ω t})]$
Hence (C) + Detailed solution of differential equation
$\Rightarrow a = ω^{2} r = v \frac{d v}{d r} \Rightarrow \int_{0}^{v} v d v = ω^{2} \int_{R / 2}^{F} r d r$
$\Rightarrow \frac{v^{2}}{2} = ω^{2} [\frac{r^{2}}{2} - \frac{R^{2}}{8}] \Rightarrow v = ω \sqrt{r^{2} - \frac{R^{2}}{4}} = \frac{d r}{d t}$
$\Rightarrow ln [\frac{r + \sqrt{x^{2} - R^{2} / 4}}{R / 2}] = ω t \Rightarrow r + \sqrt{r^{2} - R^{2} / 4} = \frac{R}{2} e^{ω t}$
$\Rightarrow r^{2} - \frac{R^{2}}{4} = {[\frac{R}{2} e^{ω t} - R]}^{2} \Rightarrow r^{2} - \frac{R^{2}}{4} = [\frac{R}{2} e^{ω t + r^{2}} - R . r e^{ω t}]$
$\Rightarrow r R e^{ω t} = R \frac{o^{2}}{4} [1 + e^{2 ω t}] \Rightarrow r = \frac{R}{4} [e^{ω t} + e^{- ω t}]$

Updated on:21/07/2023

|

Class 12 PHYSICS ROTATIONAL MOTION

Topper's Solved these Questions

Similar Questions

VMC MODULES ENGLISH-ROTATIONAL MOTION -JEE Advanced (Archive) (LINKED COMPREHENSIVE TYPE)

Home
Ask Doubt
Profile