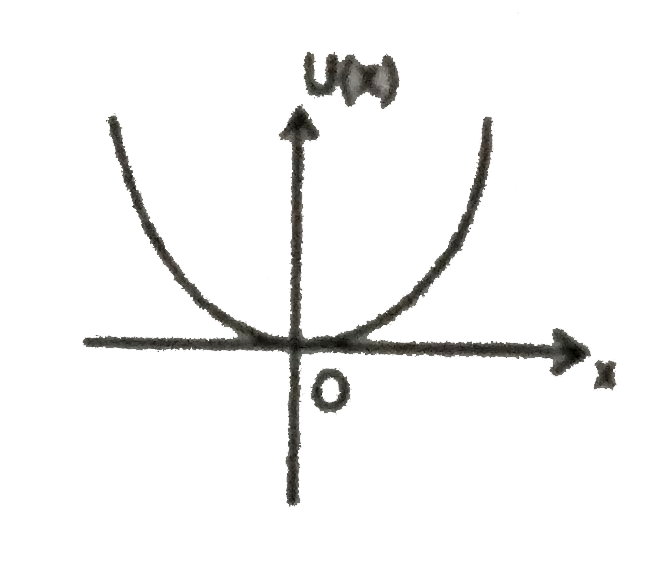
Figure shows a plot of potential energy function U(x)=kx2 where x=displacement and k=constant. Identify the correct conservative force function F(x)
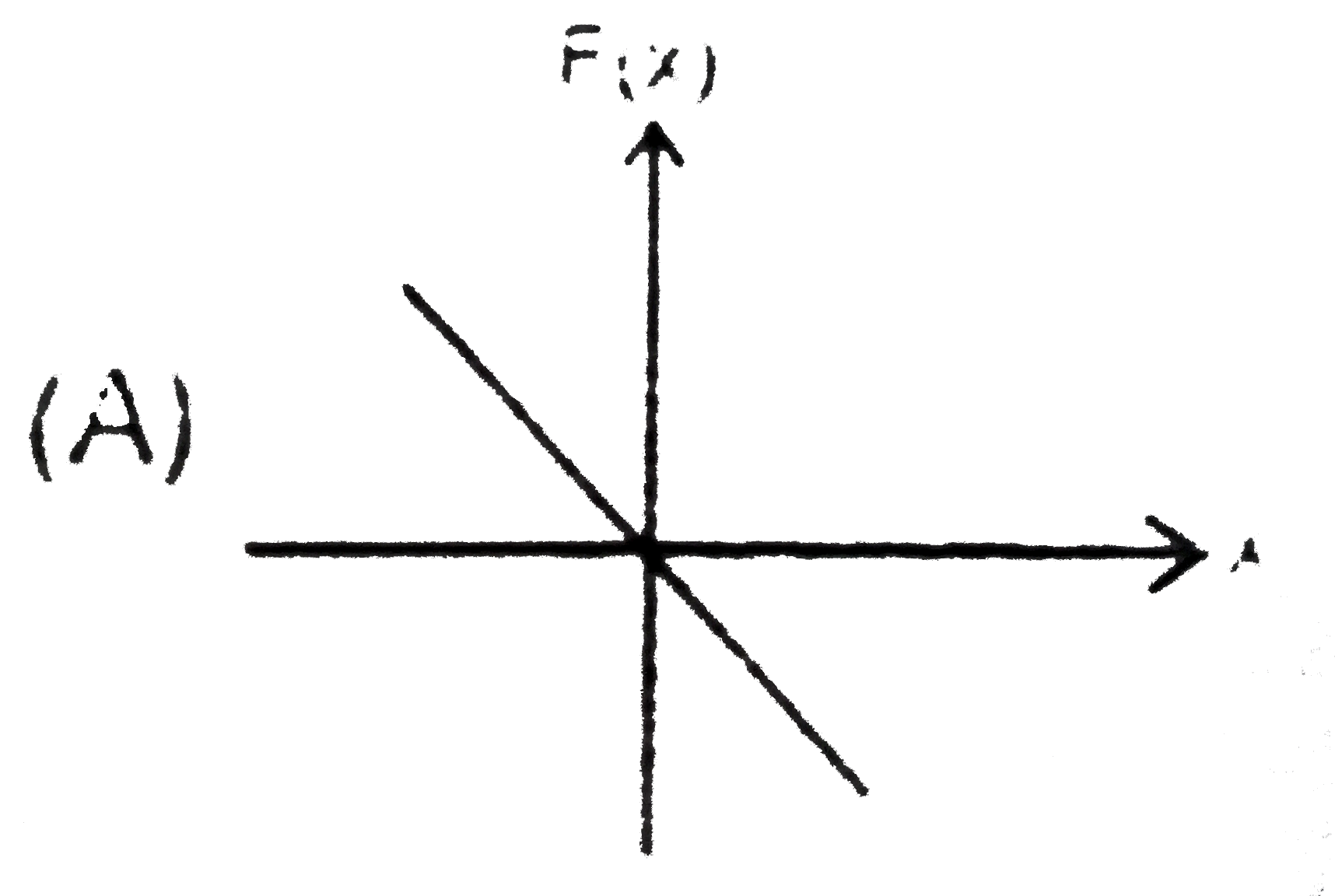
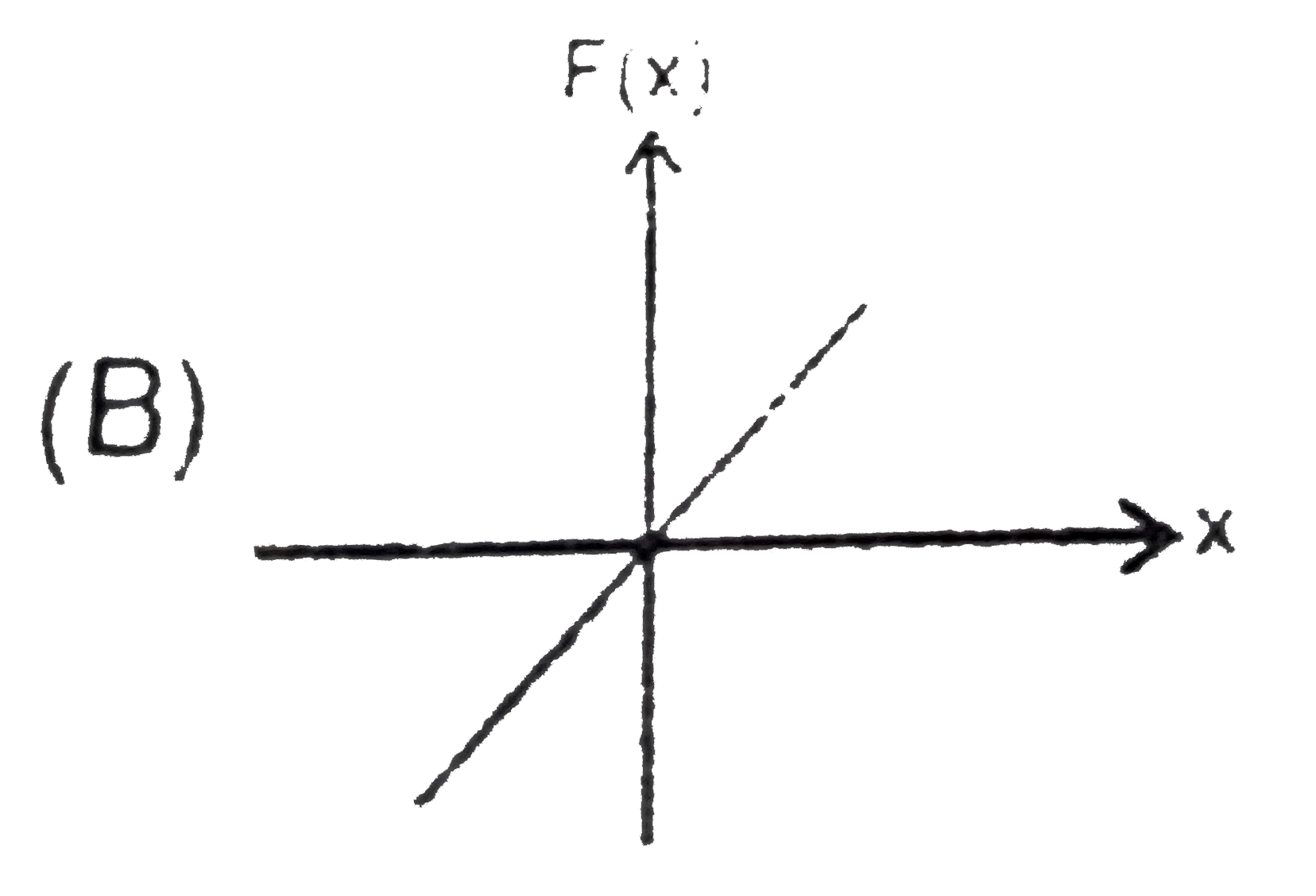
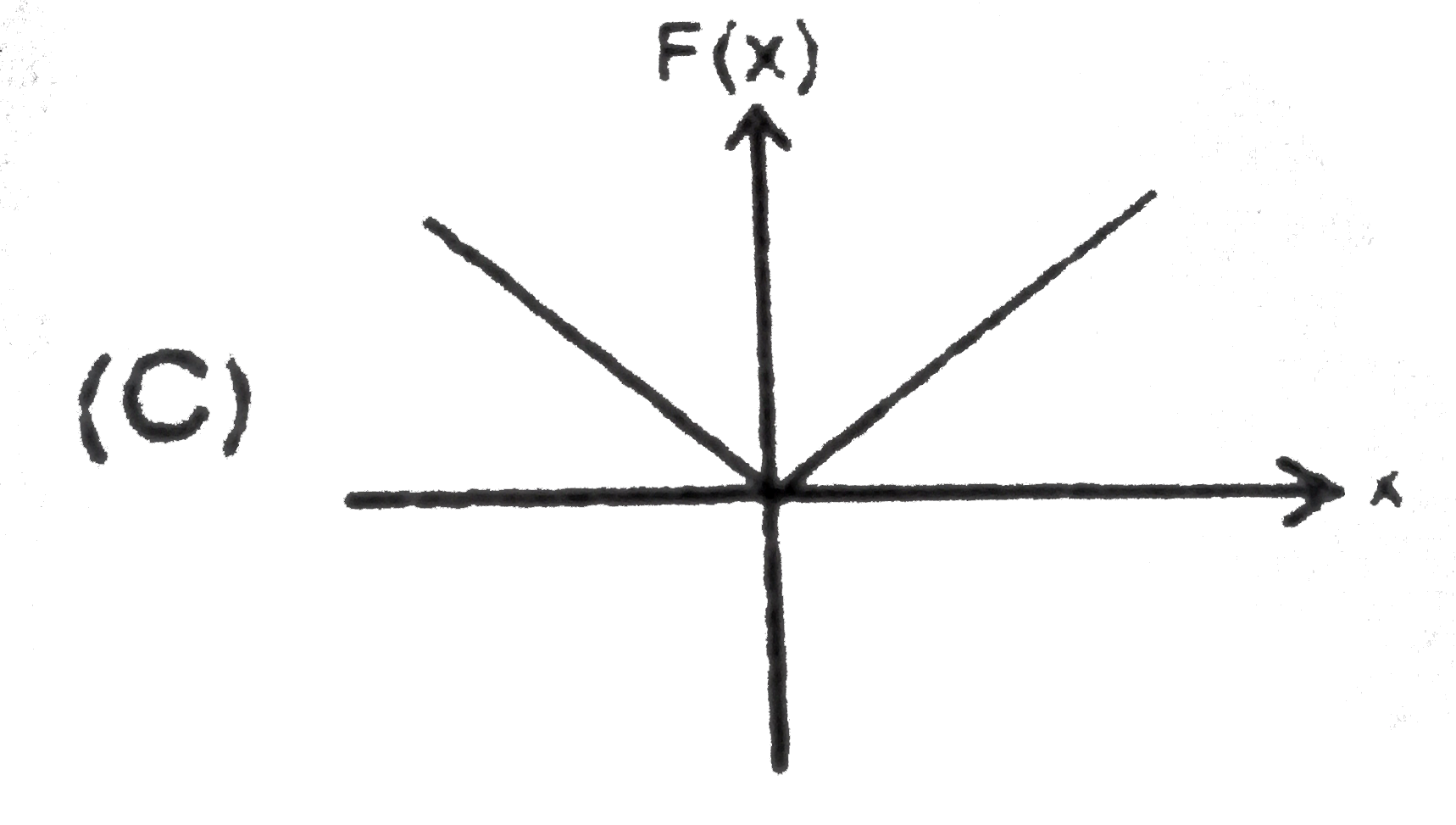

The correct Answer is:A
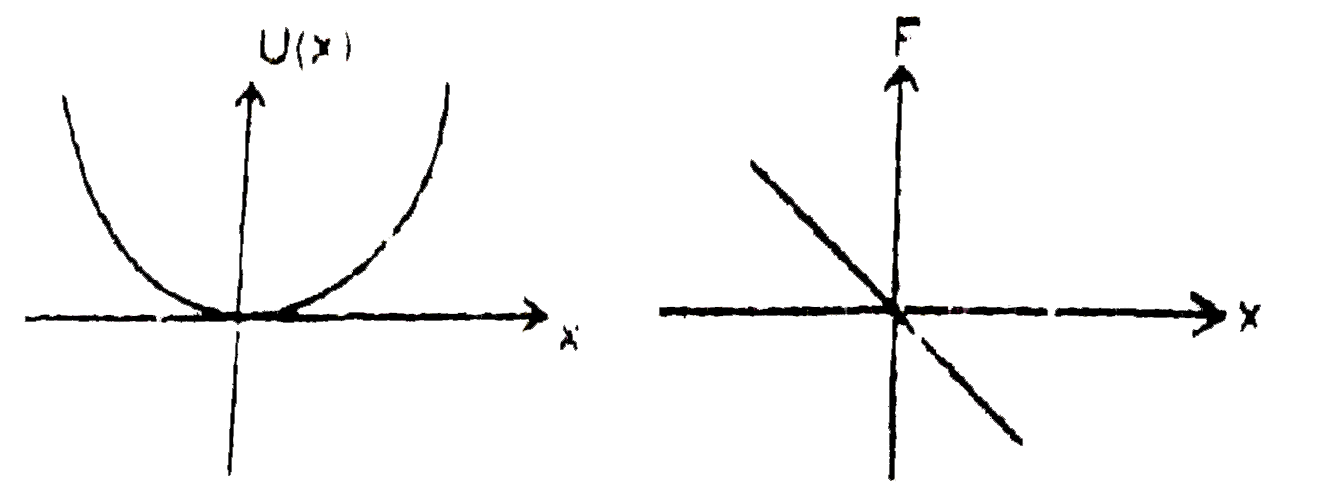
F=−dUdx
∵U(x)=kx2
F=−2kx.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.349videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.3520videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.329videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)19videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
Given below is the plot of a potential energy function U(x) for a system, in which a particle is in one dimensional motion, while a conservative force F(x) acts on it. Suppose tha Emech= 8 J, the incorrect statement for this system is :
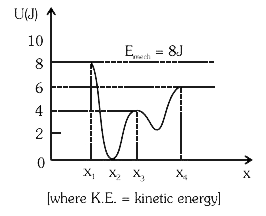
A. at x > x4, K.E. is constant throughout the region.
B. at x < x1 K.E. is smallest and the particle is moving at the slowest speed.
C. at x = x2 , K.E is greatest and the particle is moving at the fastest speed.
D. at x = x3, K.E. = 4 JView SolutionFigure shows a plot of the potential energy as a function of x for a particle moving along the x-axis. Which of the following statement(s) is/are true?
 View Solution
View SolutionFigure shows a plot of the potential energy as a function of x for a particle moving along the x-axis. Which of the following statement(s) is/are true?
 View Solution
View SolutionThe potential energy function of a particle in the x-y plane is given by U=k(x+y), where (k) is a constant. The work done by the conservative force in moving a particlae from (1,1) to (2,3) is .
View SolutionA particle located in one dimensional potential field has potential energy functionU(x)=ax2−bx3, where a and b are positive constants. The position of equilibrium corresponds to x equal to
View SolutionThe potential energy U for a force field →F is such that U=−kxy where K is a constant . Then
View SolutionA particle is moving on frictionless XY-plane. It is acted on by a conservative force described by the potential-energy function.
U(x,y,z)=12k(x2+y2+z2)
where , k=constant
Derive an expression for the force an the particle.View SolutionThe potential energy of a body is given by U=A−Bx2 (where x is the displacement). The magnitude of force acting on the partical is
View SolutionA particle located in a one-dimensional potential field has its potential energy function as U(x)ax4−bx2, where a and b are positive constants. The position of equilibrium x corresponds to
View SolutionThe potential energy U of diatomic molecules as a function of separation r is shown in figure. Identify the correct stateement.
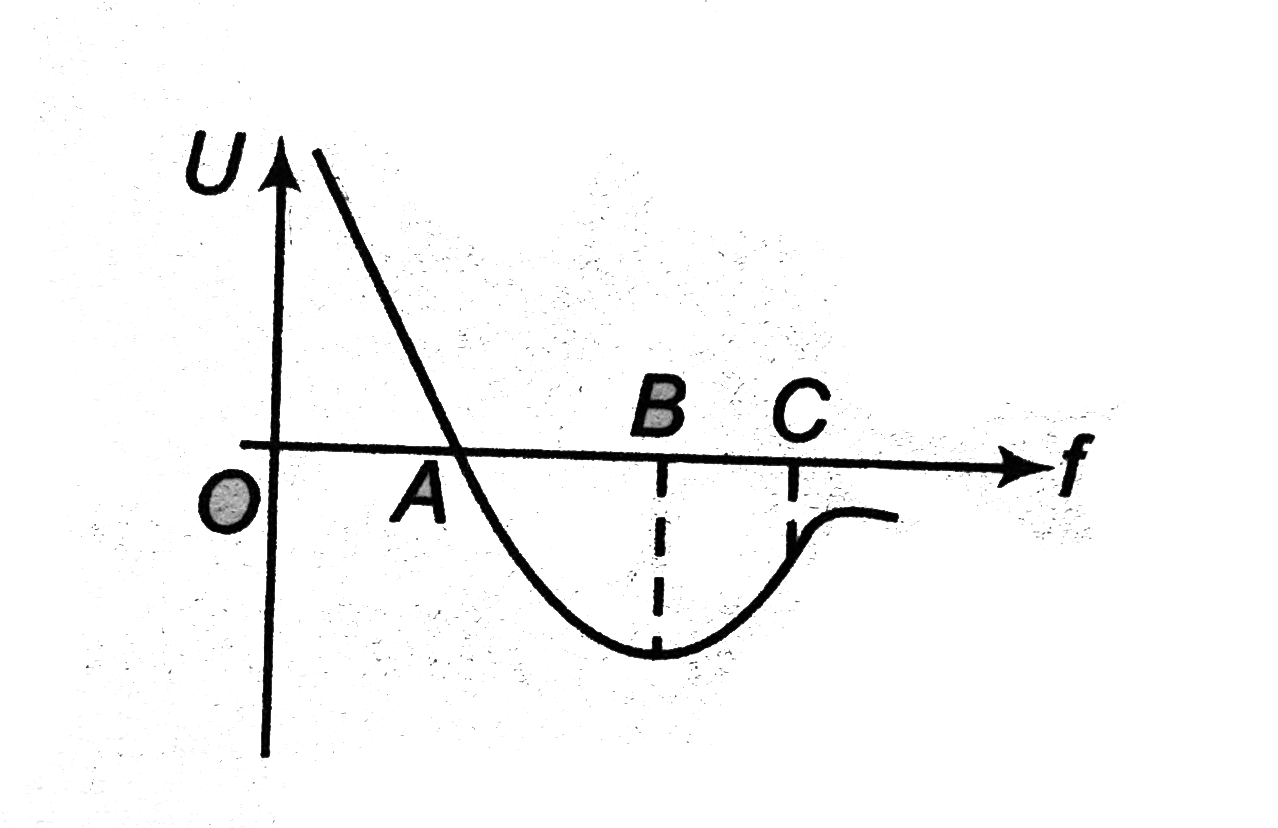 View Solution
View Solution

