A particle moves from point P(1,2,3) to (2,1,4) under the action of a constant force F=(2ˆi+ˆj+ˆk)N. Work done by the force is
2 J
4 J
16 J
8 J
The correct Answer is:A
To find the work done by the force when a particle moves from point P(1,2,3) to point Q(2,1,4) under the action of a constant force F=2^i+^j+^k N, we can follow these steps:
Step 1: Determine the Displacement Vector
The displacement vector d can be calculated by subtracting the initial position vector from the final position vector.
1. Initial Position Vector P:
P=1^i+2^j+3^k
2. Final Position Vector Q:
Q=2^i+1^j+4^k
3. Displacement Vector d:
d=Q−P=(2^i+1^j+4^k)−(1^i+2^j+3^k)
d=(2−1)^i+(1−2)^j+(4−3)^k=1^i−1^j+1^k
Step 2: Calculate Work Done
The work done W by the force is given by the dot product of the force vector F and the displacement vector d.
1. Force Vector F:
F=2^i+1^j+1^k
2. Dot Product F⋅d:
W=F⋅d=(2^i+1^j+1^k)⋅(1^i−1^j+1^k)
=2⋅1+1⋅(−1)+1⋅1
=2−1+1=2 joules
Final Answer
The work done by the force is 2 joules.
---
The displacement vector d can be calculated by subtracting the initial position vector from the final position vector.
P=1^i+2^j+3^k
Q=2^i+1^j+4^k
d=Q−P=(2^i+1^j+4^k)−(1^i+2^j+3^k)
d=(2−1)^i+(1−2)^j+(4−3)^k=1^i−1^j+1^k
The work done W by the force is given by the dot product of the force vector F and the displacement vector d.
F=2^i+1^j+1^k
W=F⋅d=(2^i+1^j+1^k)⋅(1^i−1^j+1^k)
=2⋅1+1⋅(−1)+1⋅1
=2−1+1=2 joules
The work done by the force is 2 joules.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:Assignment (SECTION - A)
Explore 64 Videos
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:Assignment (SECTION - B)
Explore 35 Videos
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:SECTION-J (AAKASH CHALLENGERS QUESTIONS)
Explore 14 Videos
- WAVESBook:AAKASH INSTITUTE ENGLISHChapter:WAVESExercise:ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
Explore 12 Videos
Similar Questions
A particle moves from point (ˆi+ˆj)m to a point (6ˆi−2ˆj)m under the action of force (10ˆi−2ˆj)N. The work done by the force is
View SolutionAn object is displaced from point A(2m,3m,4m) to a point B(1m,2m,3m) under a constant force F=(2ˆi+3ˆj+4ˆk)N. Find the work done by this force in this process.
View SolutionAn object is displaced from point A(2m,3m,4m,) to a point B (1m,2m,3m) under a constant force (2ˆi+3ˆj+4ˆk) N. Find the work done by this force in this process.
View SolutionA body moves from a position →r1=(2ˆi−3ˆj−4ˆk) m to a position →r2=(3ˆi−4ˆj+5ˆk)m under the influence of a constant force →F=(4ˆi+ˆj+6ˆk)N. The work done by the force is :
View SolutionA particle is displaced from a position 2ˆi−ˆj+ˆk(m) to another position 3ˆi+2ˆj−2ˆk(m) under the action of a force 2ˆi+ˆj−ˆk(N). The work done by the force is
View SolutionA block of mass m is taken from A to B under the action of a constant force F. Work done by this force is
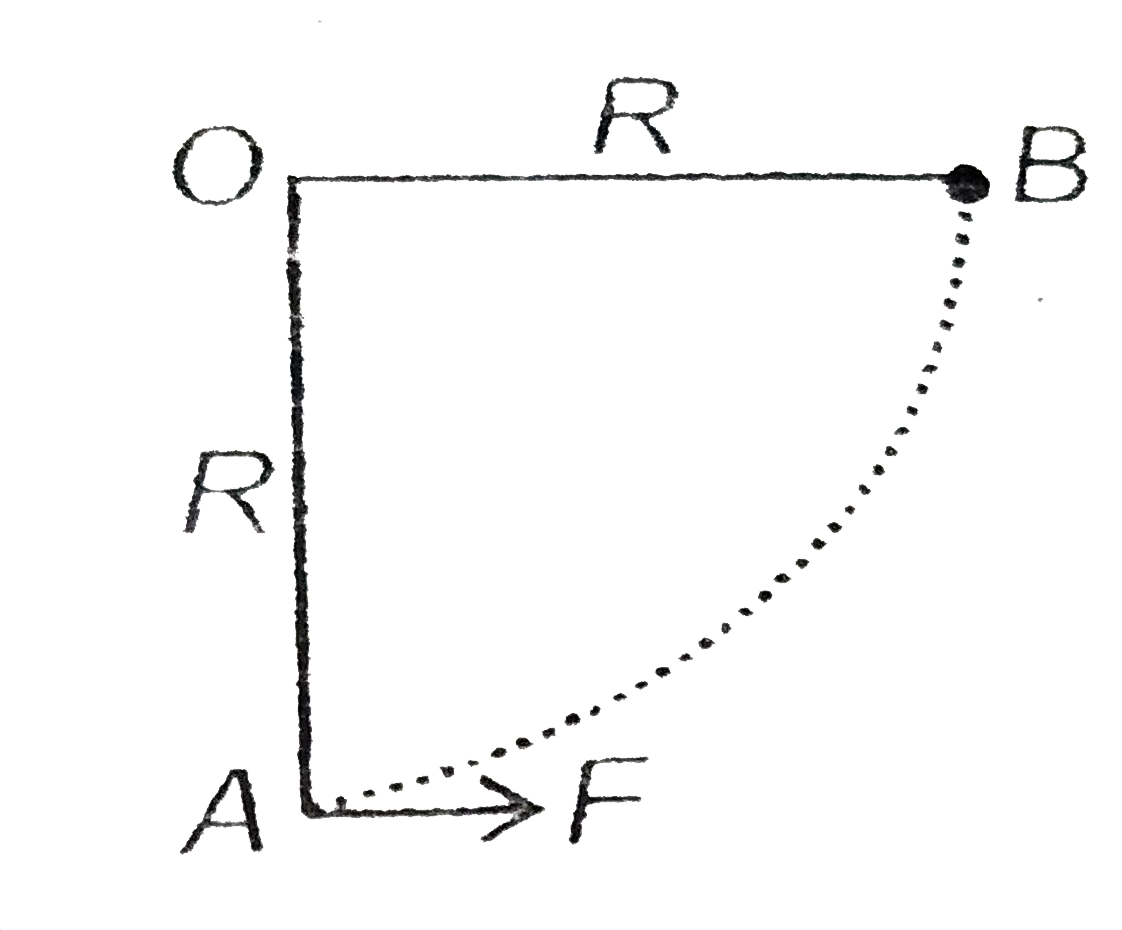
View SolutionA block is displaced from (1m,4m,6m) to (2ˆi+3ˆj−4ˆk)m under a constant force F=(6ˆi−2ˆj+ˆk)N. Find the work done by this force.
View SolutionA particle is desplaced from a position (2ˆI+4ˆ−3ˆk) metre to another position (12ˆi+14ˆj+7ˆk) metre under the action of force (ˆi+2ˆj−ˆk) metre under rthe action of force (ˆi+2ˆj−ˆk) N. Work done by the force is
View SolutionA particle moves along x - axis under the action of a position dependent force F=(5x2−2x)N. Work done by force on the particle when it moves from origin to x = 3 m is
View SolutionA particle moves with a velocity of (4ˆi−2ˆj+2ˆk)ms−1 under the influence of a constant force →F=(10ˆi+3ˆj−2ˆk)N. The instantaneous power applied to the particle is
View Solution