What is the minimum velocity with which a body of mass m must enter a vertical loop of radius R so that it can complete the loop?
The correct Answer is:A
To find the minimum velocity u with which a body of mass m must enter a vertical loop of radius R to complete the loop, we can follow these steps:
Step 1: Analyze the forces at the top of the loop
At the highest point of the loop, the forces acting on the body are:
- The gravitational force mg acting downward.
- The centripetal force required to keep the body moving in a circular path, which is provided by the gravitational force and the tension in the string (if any). For the minimum condition, we can assume the tension is zero.
At the top of the loop, the centripetal force is given by:
mv2R
where v is the velocity at the top of the loop.
For the body to just complete the loop, the gravitational force must provide the necessary centripetal force:
mg=mv2R
This simplifies to:
g=v2R
From this, we can express v as:
v=√gR
Step 2: Apply conservation of mechanical energy
Now, we will use the conservation of mechanical energy to find the minimum velocity u at the bottom of the loop. The total mechanical energy at the bottom must equal the total mechanical energy at the top.
At the bottom of the loop:
- Potential energy UA=0 (taking this point as the reference level).
- Kinetic energy KA=12mu2.
At the top of the loop:
- Potential energy UB=mg(2R) (the height is 2R).
- Kinetic energy KB=12mv2.
Using conservation of energy:
UA+KA=UB+KB
Substituting the values:
0+12mu2=mg(2R)+12mv2
Step 3: Substitute v from Step 1
Now, substituting v=√gR into the energy equation:
12mu2=mg(2R)+12m(√gR)2
This simplifies to:
12mu2=mg(2R)+12mgR
12mu2=mg(2R+12R)
12mu2=mg(52R)
Step 4: Solve for u
Now, we can cancel m from both sides (assuming m≠0):
12u2=g52R
Multiplying both sides by 2:
u2=5gR
Taking the square root:
u=√5gR
Final Answer
The minimum velocity u with which a body of mass m must enter a vertical loop of radius R to complete the loop is:
u=√5gR
At the highest point of the loop, the forces acting on the body are:
- The gravitational force mg acting downward.
- The centripetal force required to keep the body moving in a circular path, which is provided by the gravitational force and the tension in the string (if any). For the minimum condition, we can assume the tension is zero.
mv2R
where v is the velocity at the top of the loop.
mg=mv2R
This simplifies to:
g=v2R
From this, we can express v as:
v=√gR
Now, we will use the conservation of mechanical energy to find the minimum velocity u at the bottom of the loop. The total mechanical energy at the bottom must equal the total mechanical energy at the top.
- Potential energy UA=0 (taking this point as the reference level).
- Kinetic energy KA=12mu2.
- Potential energy UB=mg(2R) (the height is 2R).
- Kinetic energy KB=12mv2.
UA+KA=UB+KB
Substituting the values:
0+12mu2=mg(2R)+12mv2
Now, substituting v=√gR into the energy equation:
12mu2=mg(2R)+12m(√gR)2
This simplifies to:
12mu2=mg(2R)+12mgR
12mu2=mg(2R+12R)
12mu2=mg(52R)
Now, we can cancel m from both sides (assuming m≠0):
12u2=g52R
Multiplying both sides by 2:
u2=5gR
Taking the square root:
u=√5gR
The minimum velocity u with which a body of mass m must enter a vertical loop of radius R to complete the loop is:
u=√5gR
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - D)
13 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - B)
35 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
A ball of mass m is attached to one end of a light rod of length l, the other end of which is hinged. What minimum velocity v should be imparted to the ball downwards, so that it can complete the circle ?

View SolutionA cabin is moving upwards with a constant acceleration g. A boy standing in the cabin wants to whirl a particle of mass m in a vertical circle of radius l. (Mass is attached to an ideal string.) Calculate minimum velocity which should be provided at lowermost point (w.r.t cabin) so that particle can just complete the circle.
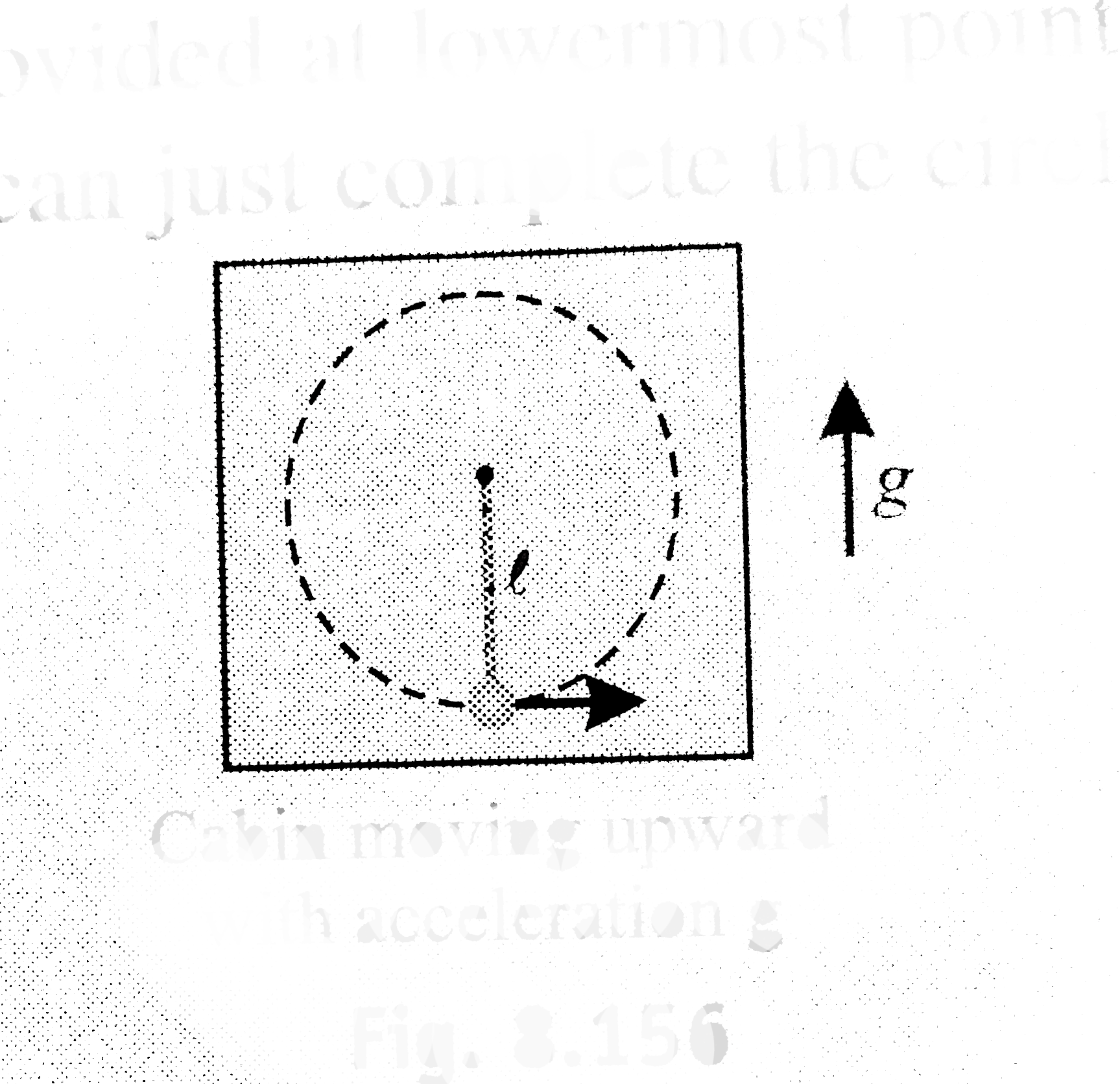
View SolutionYou may have seen in a circus a motorcyclist driving in vertical loops inside a death well (a hollow spherical chamber with holes, so the spectators can watch from outside). Explain clearly why the motorcyclist does not drop down when he is at the uppermost point of death well with no support from below. What is the minimum speed required at the uppermost position to perform a vertical loop if the radius of the chamber is 25 m ?
View SolutionWith what velocity a body of mass m be projected vertically upwards so that it may be able to reach a height nR above earth's surface
View SolutionAn inclined track ends in a circular loop of radius r. From what height on the track a particle should be released so that it completes the loop, assuming there is no friction ?
View SolutionThe velocity of a body of mass m revolving in a vertical circle of radius R at the lowest point 2√2gR . The minimum tension in the string will be
View SolutionA rectangular conducting loop, PQRS is hanging from a thread as shown. Thread is now cut. Compute velocity with which the loop falls as function of time t. Show that if side PS is large enough the loop ultimately falls with constant speed. (m = mass of loop, r = Resistance of loop, PQ = l, PS = b)

View SolutionWhat is the minimum energy required to launch a satellite of mass m from the surface of a planet of mass M and radius R in a circular orbit at an altitude of 2R?
View SolutionA particle of mass m is released from a height H on a smooth curved surface which ends into a vertical loop of radius R, as shown. Choose the correct alernative(s) if H=2R.
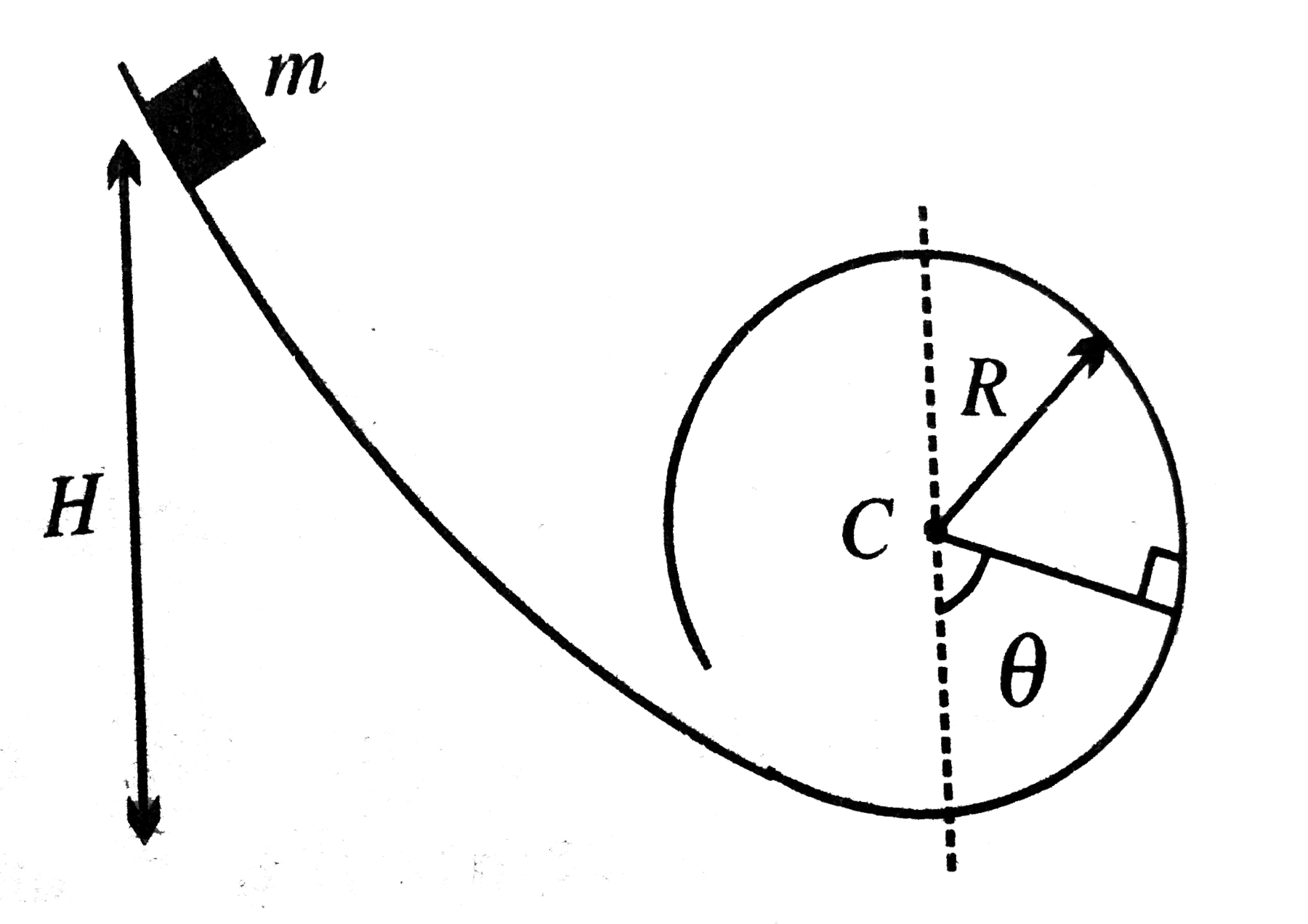
View SolutionA particle of mass m is released from a height H on a smooth curved surface which ends into a vertical loop of radius R, as shown. Choose the correct alernative(s) if H=2R.
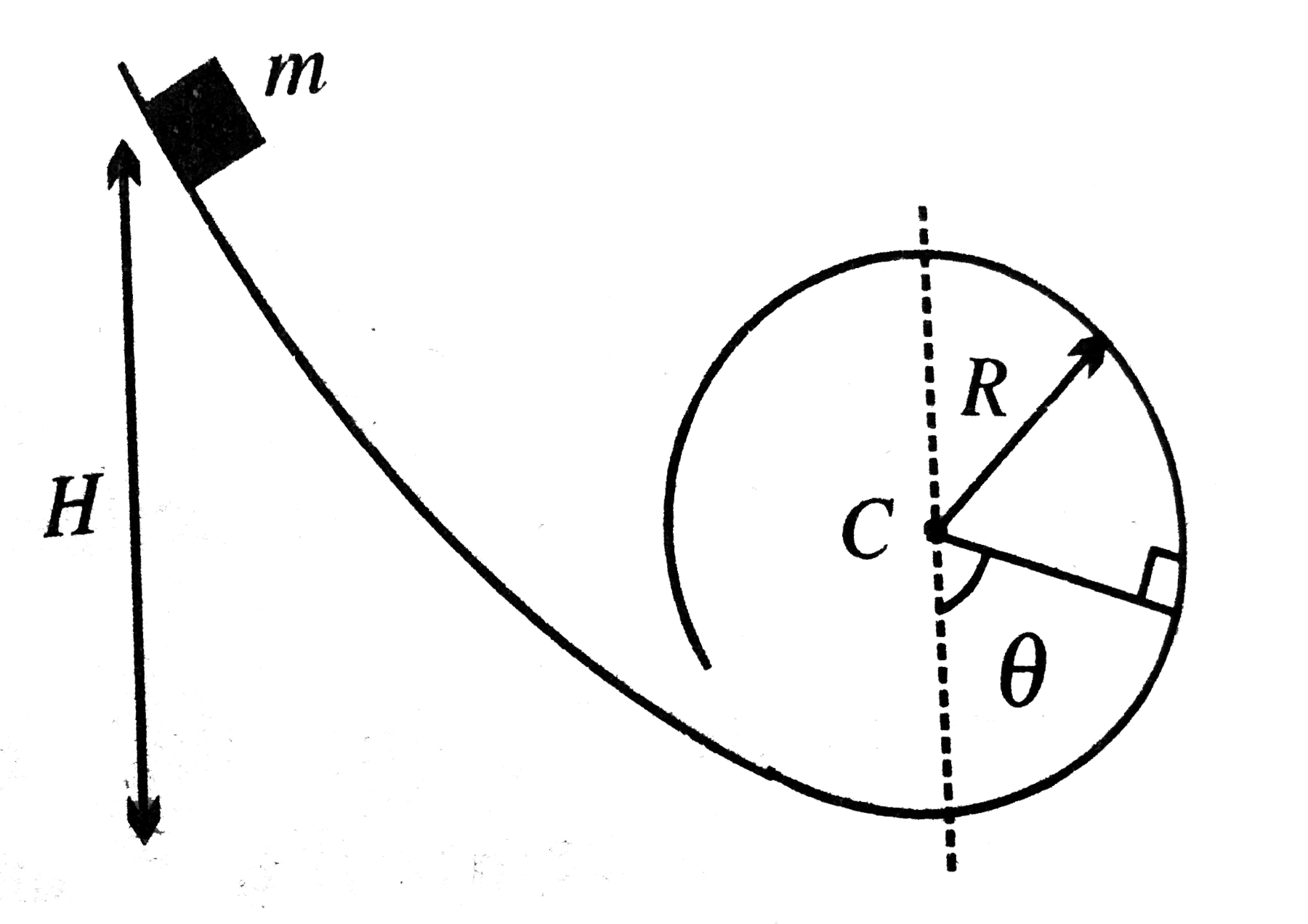
View Solution
