An inclined track ends in a circular loop of radius r. From what height on the track a particle should be released so that it completes the loop, assuming there is no friction ?
r2
3r2
2r
5r2
The correct Answer is:D
To solve the problem of determining the height from which a particle should be released on an inclined track so that it completes a circular loop of radius r, we can follow these steps:
Step 1: Understand the conditions for completing the loop
To complete the circular loop, the particle must have a minimum velocity at the top of the loop. This minimum velocity v can be derived from the centripetal force requirement. At the top of the loop, the gravitational force must provide the necessary centripetal force:
mg=mv2r
From this, we can derive the minimum velocity at the top of the loop:
v2=gr⇒v=√gr
However, this is the condition for the top of the loop. For the particle to just complete the loop, we actually need to consider the energy conservation from the starting height to the top of the loop.
Step 2: Apply conservation of energy
When the particle is released from height h, its initial potential energy is converted into kinetic energy and potential energy at the top of the loop.
The potential energy at height h is:
PEinitial=mgh
At the top of the loop (height 2r), the potential energy is:
PEtop=mg(2r)
The kinetic energy at the top of the loop is:
KEtop=12mv2
Using the minimum velocity v=√5gr at the top of the loop (derived from the centripetal force condition), we can substitute this into the kinetic energy expression:
KEtop=12m(5gr)=52mgr
Step 3: Set up the energy conservation equation
By conservation of energy, we have:
mgh=PEtop+KEtop
Substituting the expressions we derived:
mgh=mg(2r)+52mgr
Step 4: Simplify the equation
Dividing through by mg (assuming m≠0) gives:
h=2r+52r
Combining the terms:
h=2r+2.5r=4.5r=9r2
Step 5: Conclusion
Thus, the height h from which the particle should be released is:
h=5r2
Final Answer
The correct height from which the particle should be released to complete the loop is:
h=5r2
To complete the circular loop, the particle must have a minimum velocity at the top of the loop. This minimum velocity v can be derived from the centripetal force requirement. At the top of the loop, the gravitational force must provide the necessary centripetal force:
When the particle is released from height h, its initial potential energy is converted into kinetic energy and potential energy at the top of the loop.
By conservation of energy, we have:
Dividing through by mg (assuming m≠0) gives:
Thus, the height h from which the particle should be released is:
The correct height from which the particle should be released to complete the loop is:
Similar Questions
A block is released from rest at the top of an inclined plane which later curves into a circular track of radius r as shown in figure. Find the minimum height h from where it should be released so that it is able to complete the circle.
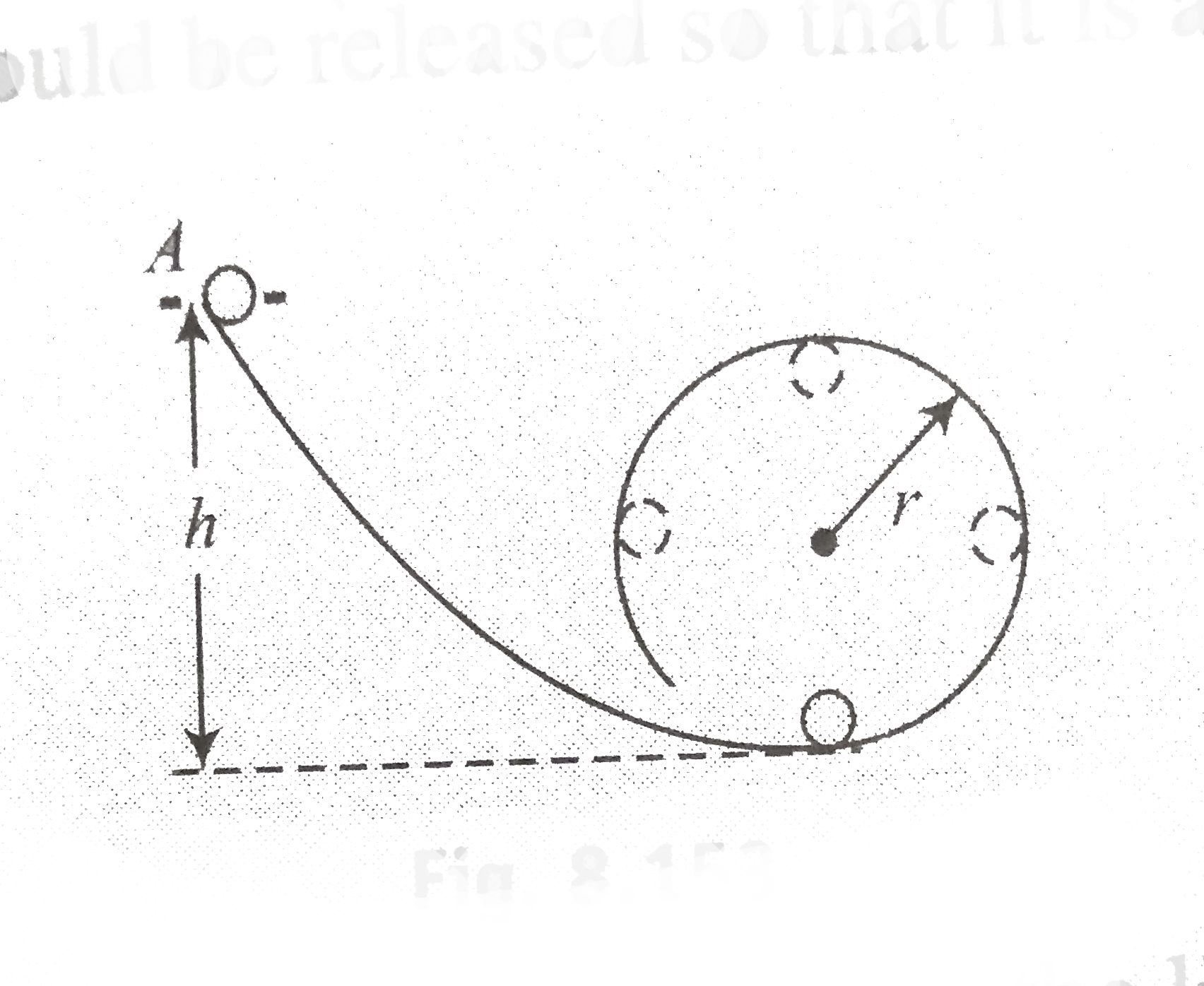
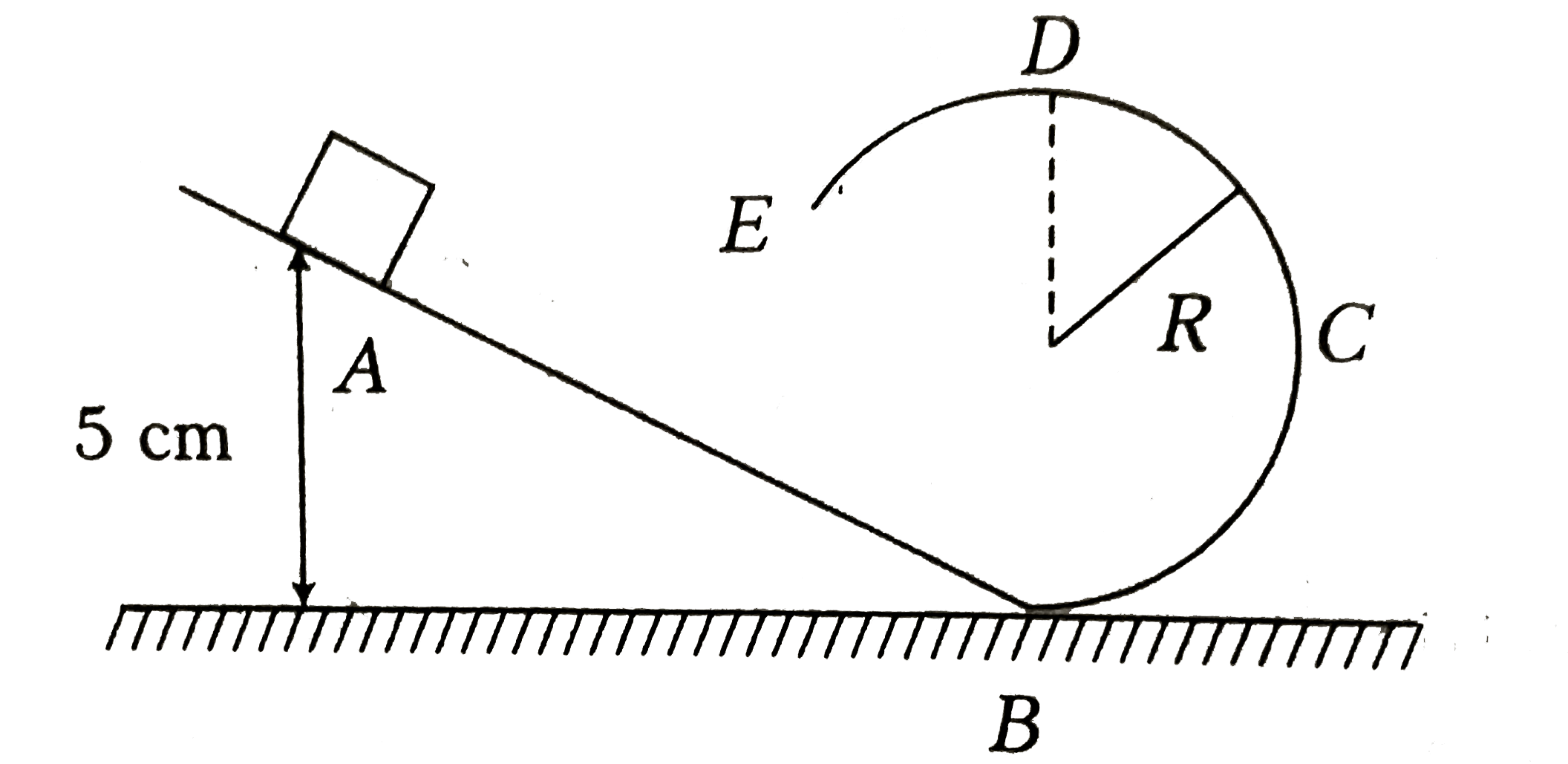
View SolutionA frictionless track ABCDE ends in a circular loop of radius R. A body slides down the track from point A which is at height h = 5cm. Maximum value of R for a body to complete the loop successfully is
View SolutionA body slides down on a frictionless track which ends in a circular loop of diameter D. The minimum height h in terms of D so that the body may just complete the circular loop, is

View SolutionWhat is the minimum velocity with which a body of mass m must enter a vertical loop of radius R so that it can complete the loop?
View SolutionWhat is the minimum velocity with which a body of mass m must enter a vertical loop of radius R so that it can complete the loop?
View SolutionA current I flows along a round circular loop of radius R. Find the line integration of magnetic field along the axis of the loop from center to ∞
View SolutionAn object of mass m is released from rest at a height h above the surface of a table. The object slides along the inside of the loop. The loop track consisting of a ramp and a circular loop of radius R shown in the figure. Assume that the track is frictionless. When the object is at the top of the circular track it pushes against the track with a force equal to three times its weight. What height was the object dropped from?

View SolutionThe moment of inertia of a circular loop of radius R, at a distance of R/2 around a rotating axis parallel to horizontal diameter of loop is
View SolutionA wire of length 'I' is bent into a circular loop of radius R and carries a current I. The magnetic field at the centre of the loop is 'B '. The same wire is now bent into a double loop. If both loops carry the same current I and it is in the same direction, the magnetic field at the centre of the double loop will be
View SolutionDue to the flow of current in a circular loop of radius R, the magnetic induction produced at the centre of the loop is B. The magnetic moment of the loop is (μ0=permeability constant)
View Solution
