What is the angle between velocity vector and acceleration vector in unitorm circular motion ?
0∘
180∘
90∘
45∘
The correct Answer is:C
Step by step video & image solution for What is the angle between velocity vector and acceleration vector in unitorm circular motion ? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
A particle starts traveling on a circle with constant tangential acceleration. The angle between velocity vector and acceleration vector, at the moment when particle completes half the circular track, is
View SolutionA particle starts travelling on a circle with constant tangential acceleration. The angle between velocity vector and acceleration vector, at the moment when particle completes half the circular track. Is
View Solution
Knowledge Check
- Question 1 - Select One
Velocity vector and acceleration vector in a uniform circular motion are related as
Aboth in the same directionBperpendicular to each otherCboth in opposite directionDnot related to each other - Question 2 - Select One
In case of a projectile motion, what is the angle between the velocity and acceleration at the highest point?
A0∘B45∘C90∘D180∘
Assertion In projectile motion, the angle between instanteneous velocity vector and acceleration vector can be anything between o to π (excluding the limiting case)
Reason In projectile motion, acceleration vector is always pointing vertically downwards. (Neglect air friction.)View SolutionA disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity. The angle between the velocity and acceleration vectors of point P is
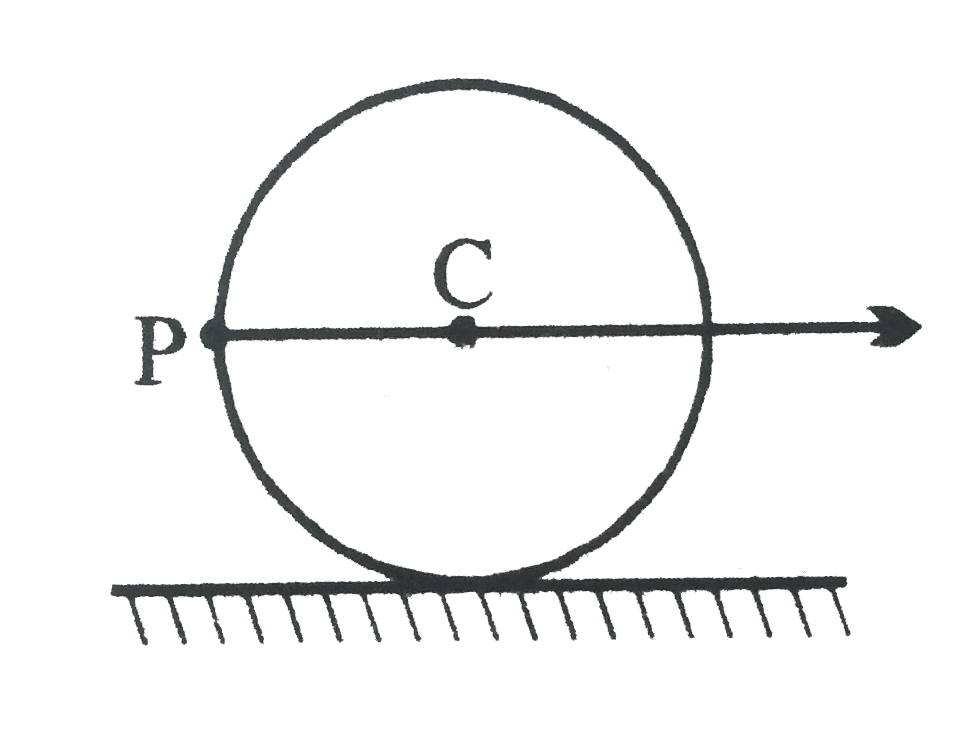.View SolutionMatch the following.
At a certain moment in time the angle between the velocity →v of a particle and the acceleration vector a of that particle is 0. Match the type of motion of the particle at this moment for different θ is
View Solutionif θ is angle between the velocity and acceleration of a particle moving on a circular path with decreasing speed, then
View Solution
A disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity the angle between the velocity ad acceleration vectors of point P isView SolutionA disc of radius R is rolling purely on a flat horizontal, with a Constant angular velocity. The angle between the of velocity and acceleration vectors point P is given by sin−1(√2/n). What is the value of n?
View Solution