Match the following.
At a certain moment in time the angle between the velocity →v of a particle and the acceleration vector a of that particle is 0. Match the type of motion of the particle at this moment for different θ is

The correct Answer is:A to (q,s); B to (q,r),C to (q),D to (p,s)
Step by step video & image solution for Match the following. At a certain moment in time the angle between the velocity vecv of a particle and the acceleration vector a of that particle is 0. Match the type of motion of the particle at this moment for different theta is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
What is the angle between velocity vector and acceleration vector in unitorm circular motion ?
View SolutionA graph between the square of the velocity of a particle and the distance s moved by the particle is shown in the figure. The acceleration of the particle is
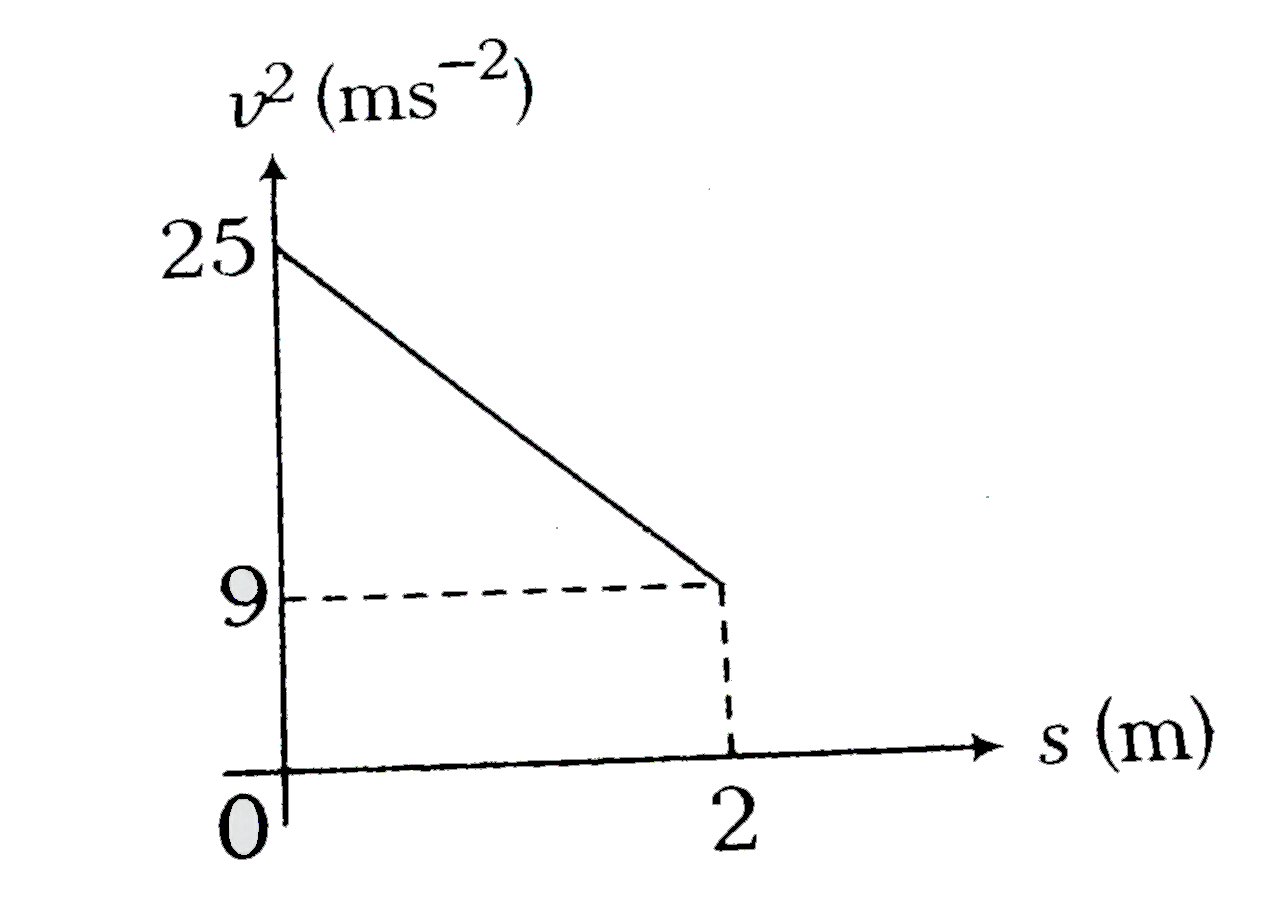 View Solution
View Solutionif θ is angle between the velocity and acceleration of a particle moving on a circular path with decreasing speed, then
View SolutionThe velocity - time graph is shown in the figure, for a particle. The acceleration of particle is
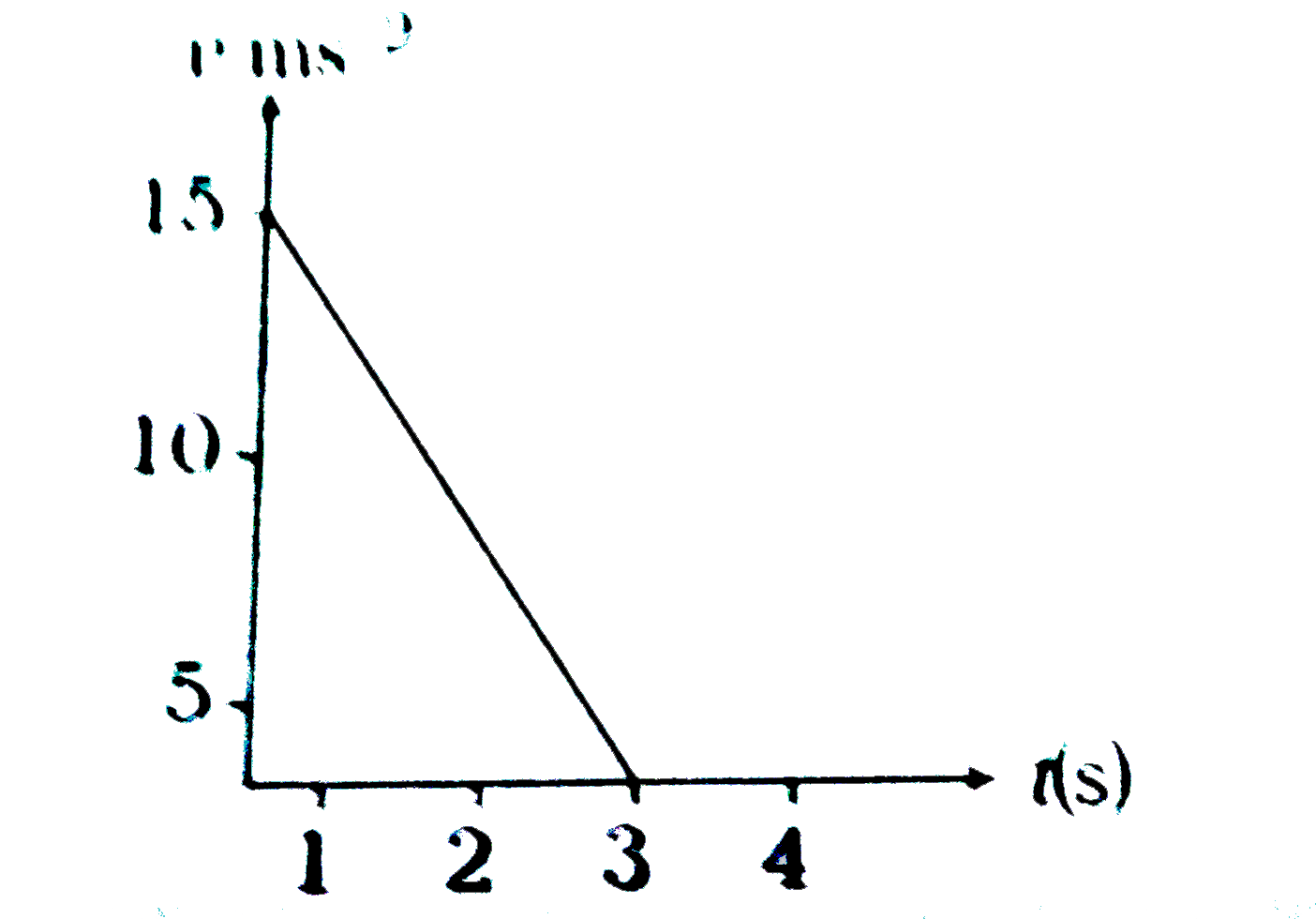 View Solution
View SolutionA particle starts travelling on a circle with constant tangential acceleration. The angle between velocity vector and acceleration vector, at the moment when particle completes half the circular track. Is
View SolutionA particle starts traveling on a circle with constant tangential acceleration. The angle between velocity vector and acceleration vector, at the moment when particle completes half the circular track, is
View SolutionInitial velocity and acceleration of a particles are as shown in the figure. Acceleration vector of particle remain constant. Then radius of curvature of path of particle :
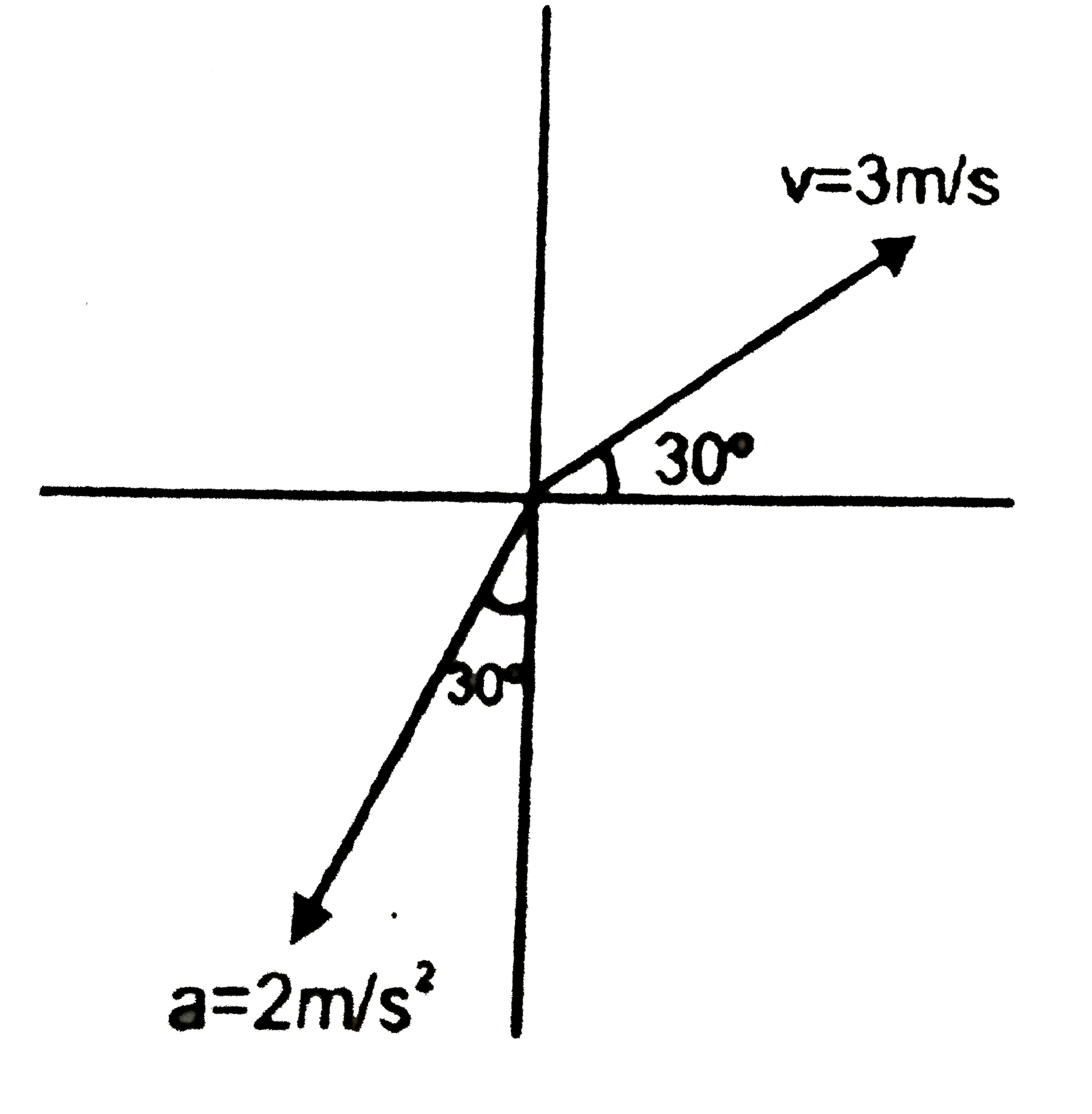 View Solution
View SolutionWhich of the following are not correctly matched with the bonds found between the constituents particle?
View SolutionMatch the following: (P = momentum of particle, K = kinetic energy of particle)
 View Solution
View SolutionMatch the following: (P = momentum of particle, K = kinetic energy of particle)
 View Solution
View Solution

