Question

Let $\theta$ be the angle between vectors $\overrightarrow{A}\text{and}\overrightarrow{B}$ . Which of the following figures correctly represent the angle $\theta$ ?

Options

A.
B.
C.
D.

Answer

C

Explanation

To determine which figure correctly represents the angle $\theta$ between the vectors $\overrightarrow{A}$ and $\overrightarrow{B}$, we can follow these steps:

Step 1: Understand the Definition of Angle Between Vectors
The angle between two vectors is defined as the angle formed when the two vectors are placed with their tails (starting points) at the same point.

Step 2: Analyze Each Option
We need to analyze each option provided to see if they correctly represent the angle `theta` between the two vectors.

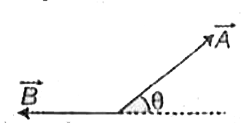
Option 1:
- Vectors `vecA` and `vecB` are shown with an angle labeled as `theta`.
- However, the angle shown is actually `180 - theta` because it is the exterior angle.
- Conclusion: Incorrect representation.

Option 2:
- Vectors `vecA` and `vecB` are again shown with an angle labeled as `theta`.
- Similar to the first option, this angle is also `180 - theta`.
- Conclusion: Incorrect representation.

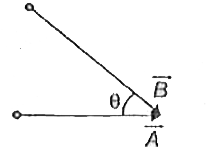
Option 3:
- This option shows both vectors with their heads touching and an angle labeled `theta`.
- However, this does not represent the angle between the two vectors correctly since the angle should be measured from their tails.
- Conclusion: Incorrect representation.

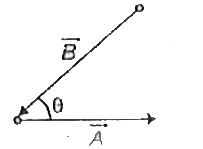
Option 4:
- This option shows vector `vecA` and vector `vecB` with their tails at the same point and an angle labeled as `theta`.
- This is the correct representation of the angle between the two vectors.
- Conclusion: Correct representation.

Step 3: Final Conclusion
After analyzing all the options, we find that only Option 4 correctly represents the angle `theta` between vectors `vecA` and `vecB`.