A particle is projected from ground with speed 80 m/s at an angle 30∘ with horizontal from ground. The magnitude of average velocity of particle in time interval t = 2 s to t = 6 s is [Take g = 10 m/s2]
40√2 m/s
40 m/s
zero
40√3 m/s
The correct Answer is:D
Step by step video & image solution for A particle is projected from ground with speed 80 m/s at an angle 30^(@) with horizontal from ground. The magnitude of average velocity of particle in time interval t = 2 s to t = 6 s is [Take g = 10 m//s^(2)] by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A particle is projected from ground with velocity 40√2m/s at 45∘. At time t=2s
View SolutionA particle is projected with speed 20ms−1 at an angle 30∘ With horizontal. After how much time the angle between velocity and acceleration will be 90∘
View SolutionA particle is projected from ground at angle 45∘ with initial velocity 20(√2)m/s. Find
(a) change in velocity,
(b) magnitude of average velocity in a time interval from t=0 to t=3s.
View SolutionA particle is projected with velocity 50 m/s at an angle 60∘ with the horizontal from the ground. The time after which its velocity will make an angle 45∘ with the horizontal is
View SolutionA particle is projected with speed u at angle θ with horizontal from ground . If it is at same height from ground at time t1andt2 , then its average velocity in time interval t1 to t2 is
View SolutionAn object is projected from ground with speed 20 m/s at angle 30∘ with horizontal. Its centripetal acceleration one second after the projection is
[ Take g = 10 m/s2 ]
View SolutionA particle is projected from ground with velocity 3ˆi+4ˆj m/s. Find range of the projectile :-
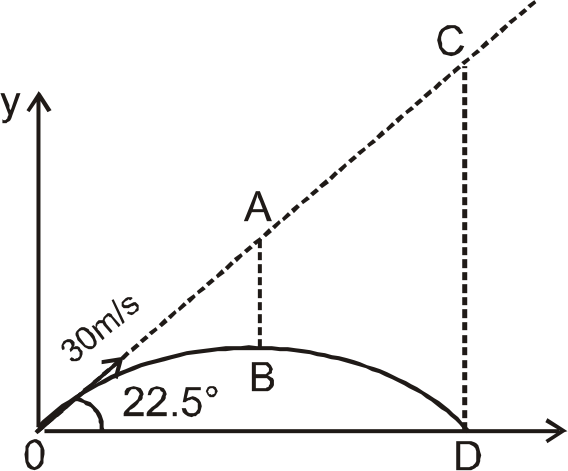
View SolutionA particle is projected with speed 30m/s at angle 22.5∘ with horizontal from ground as shown. AB and CD are parallel to y-axis and B is highest point of trajectory of particle. CD/AB is
View SolutionA particle is projected from ground with speed u and at an angle θ with horizontal. If at maximum height from ground, the speed of particle is 1/2 times of its initial velocity of projection, then find its maximum height attained.
View SolutionA particle is projected at angle θ with horizontal from ground. The slop (m) of the trajectory of the particle varies with time (t) as
View Solution
