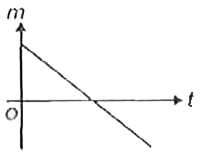
A particle is projected at angle θ with horizontal from ground. The slop (m) of the trajectory of the particle varies with time (t) as

The correct Answer is:A
To solve the problem of how the slope m of the trajectory of a particle projected at an angle θ with the horizontal varies with time t, we can follow these steps:
Step 1: Understand the motion components
A particle is projected at an initial speed u at an angle θ. The horizontal and vertical components of the initial velocity are:
- Horizontal component: ux=ucosθ
- Vertical component: uy=usinθ
Step 2: Write the equations of motion
The equations of motion for the particle can be described as follows:
- Horizontal motion:
x=ucosθ⋅t
- Vertical motion:
y=usinθ⋅t−12gt2
Step 3: Derive the equation of the trajectory
To find the trajectory equation, we eliminate time t from the equations. From the horizontal motion equation, we can express t as:
t=xucosθ
Substituting this into the vertical motion equation gives:
y=usinθ⋅(xucosθ)−12g(xucosθ)2
Simplifying this, we get:
y=xtanθ−gx22u2cos2θ
Step 4: Find the slope m
The slope m of the trajectory at any point is given by:
m=dydx
Differentiating the trajectory equation:
m=tanθ−gu2cos2θx
Step 5: Express x in terms of t
From the horizontal motion equation, we know:
x=ucosθ⋅t
Substituting this into the slope equation gives:
m=tanθ−gu2cos2θ(ucosθ⋅t)
This simplifies to:
m=tanθ−gucosθt
Step 6: Analyze the slope equation
The equation m=tanθ−gucosθt represents a straight line with:
- A y-intercept of tanθ
- A negative slope of −gucosθ
Step 7: Conclusion
The slope m decreases linearly with time t, indicating that as time progresses, the slope of the trajectory becomes less steep.
Final Answer
The graph representing the slope of the trajectory of the particle as a function of time t is a straight line with a negative slope and a positive intercept.
---
A particle is projected at an initial speed u at an angle θ. The horizontal and vertical components of the initial velocity are:
- Horizontal component: ux=ucosθ
- Vertical component: uy=usinθ
The equations of motion for the particle can be described as follows:
- Horizontal motion:
x=ucosθ⋅t
- Vertical motion:
y=usinθ⋅t−12gt2
To find the trajectory equation, we eliminate time t from the equations. From the horizontal motion equation, we can express t as:
t=xucosθ
Substituting this into the vertical motion equation gives:
y=usinθ⋅(xucosθ)−12g(xucosθ)2
Simplifying this, we get:
y=xtanθ−gx22u2cos2θ
The slope m of the trajectory at any point is given by:
m=dydx
Differentiating the trajectory equation:
m=tanθ−gu2cos2θx
From the horizontal motion equation, we know:
x=ucosθ⋅t
Substituting this into the slope equation gives:
m=tanθ−gu2cos2θ(ucosθ⋅t)
This simplifies to:
m=tanθ−gucosθt
The equation m=tanθ−gucosθt represents a straight line with:
- A y-intercept of tanθ
- A negative slope of −gucosθ
The slope m decreases linearly with time t, indicating that as time progresses, the slope of the trajectory becomes less steep.
The graph representing the slope of the trajectory of the particle as a function of time t is a straight line with a negative slope and a positive intercept.
Similar Questions
A particle is projected at an angle θ with an initial speed u.
View SolutionA heavy particle is projected with a velocity at an angle with the horizontal into the uniform gravitational field. The slope of the trajectory of the particle varies as
View SolutionA particle is projected with speed u at angle θ with horizontal from ground . If it is at same height from ground at time t1andt2 , then its average velocity in time interval t1 to t2 is
View SolutionA particle of mass m is projected with speed u at angle θ with horizontal from ground. The work done by gravity on it during its upward motion is
View SolutionA particle of mass m is projected with speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA particle of mass m is projected with speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA particle is projected at an angle θ from the horizontal with kinetic energy (T). What is the kinetic energy of the particle at the highest point ?
View SolutionA particle of mass m is projected with a velocity v at an angle of θ with horizontal. The angular momentum of the particle at the highest point of its trajectory is equal to :
View SolutionA particle is projected with velocity v at an angle θ aith horizontal. The average angle velocity of the particle from the point of projection to impact equals
View SolutionA particle is projected at an angle θ=30∘ with the horizontal, with a velocity of 10ms−1. Then
View Solution
