Three moles of an ideal gas (Cp=72R) at pressure, PA and temperature TA is isothermally expanded to twice its initial volume. It is then compressed at constant pressure to its original volume. Finally gas is compressed at constant volume to its original pressure PA.
(a) Sketch P-V and P-T diagrams for the complete process.
(b) Calculate the net work done by the gas, and net heat supplied to the gas during the complete process.

The correct Answer is:A, C
To solve the problem step by step, we will analyze the processes involved, sketch the required diagrams, and calculate the net work done and net heat supplied during the complete process.
Step 1: Understanding the Processes
1. Isothermal Expansion (A to B): The gas expands isothermally from volume VA to VB=2VA at constant temperature TA.
2. Isobaric Compression (B to C): The gas is compressed at constant pressure from volume VB back to VC=VA.
3. Isochoric Compression (C to A): The gas is compressed at constant volume back to its original pressure PA.
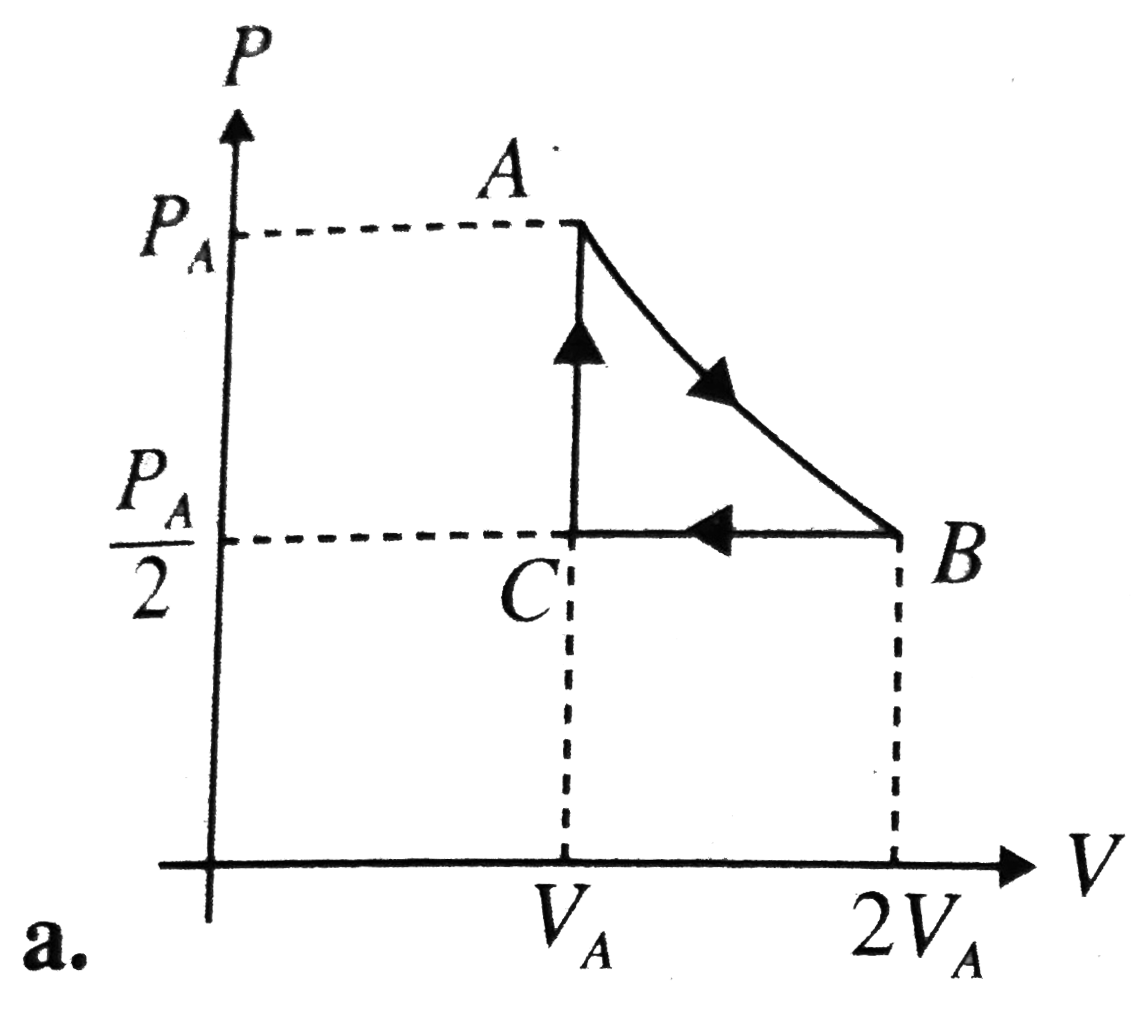
Step 2: Sketching the P-V Diagram
- Point A: (PA,VA)
- Point B: (PB,VB) where PB=PA2 and VB=2VA
- Point C: (PC,VC) where PC=PA2 and VC=VA
The P-V diagram will show:
- A hyperbolic curve from A to B (isothermal).
- A straight line from B to C (isobaric).
- A vertical line from C to A (isochoric).
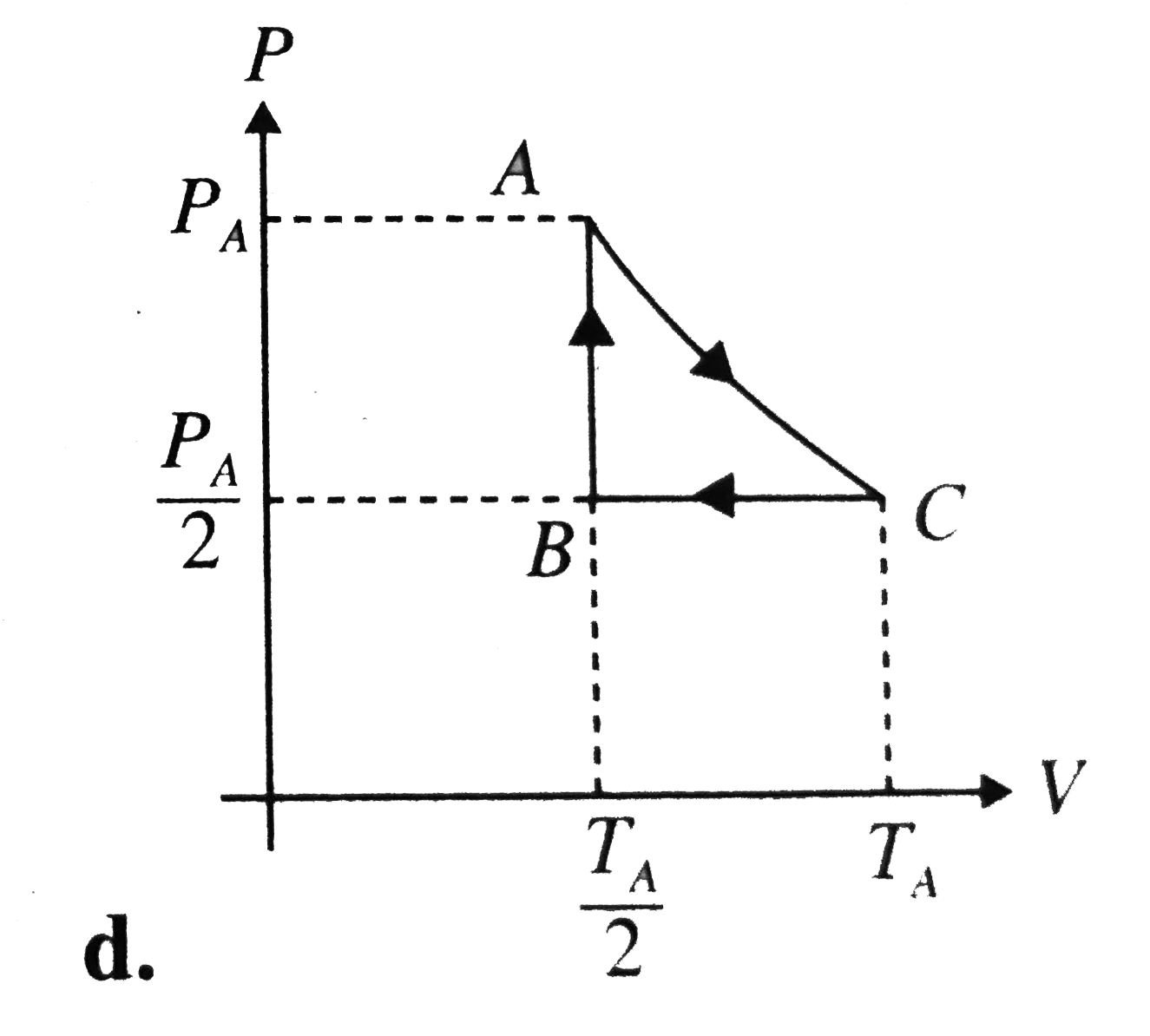
Step 3: Sketching the P-T Diagram
- Point A: (PA,TA)
- Point B: (PB,TA) where PB=PA2
- Point C: (PC,TC) where TC=TA2
The P-T diagram will show:
- A horizontal line from A to B (isothermal).
- A straight line from B to C (isobaric).
- A straight line from C to A (isochoric).
Step 4: Calculating the Work Done
1. Work Done in Isothermal Process (A to B):
WAB=nRTAln(VBVA)=3RTAln(2)
2. Work Done in Isobaric Process (B to C):
WBC=PB(VC−VB)=PA2(VA−2VA)=−PAVA2=−3RTA2
3. Work Done in Isochoric Process (C to A):
WCA=0
4. Net Work Done:
Wnet=WAB+WBC+WCA=3RTAln(2)−3RTA2+0
Step 5: Calculating the Heat Supplied
1. Heat Supplied in Isothermal Process (A to B):
QAB=WAB=3RTAln(2)
2. Heat Supplied in Isobaric Process (B to C):
- Change in Internal Energy:
ΔUBC=nCVΔT=3⋅5R2(TA2−TA)=−15RTA4
- Heat Supplied:
QBC=WBC+ΔUBC=−3RTA2−15RTA4=−21RTA4
3. Heat Supplied in Isochoric Process (C to A):
QCA=ΔUCA=nCVΔT=3⋅5R2(TA−TA2)=15RTA4
4. Net Heat Supplied:
Qnet=QAB+QBC+QCA=3RTAln(2)−21RTA4+15RTA4
Qnet=3RTAln(2)−6RTA4=3RTAln(2)−3RTA2
Final Answers
- Net Work Done:
Wnet=3RTAln(2)−3RTA2
- Net Heat Supplied:
Qnet=3RTAln(2)−3RTA2
1. Isothermal Expansion (A to B): The gas expands isothermally from volume VA to VB=2VA at constant temperature TA.
2. Isobaric Compression (B to C): The gas is compressed at constant pressure from volume VB back to VC=VA.
3. Isochoric Compression (C to A): The gas is compressed at constant volume back to its original pressure PA.
- Point A: (PA,VA)
- Point B: (PB,VB) where PB=PA2 and VB=2VA
- Point C: (PC,VC) where PC=PA2 and VC=VA
- A hyperbolic curve from A to B (isothermal).
- A straight line from B to C (isobaric).
- A vertical line from C to A (isochoric).
- Point A: (PA,TA)
- Point B: (PB,TA) where PB=PA2
- Point C: (PC,TC) where TC=TA2
- A horizontal line from A to B (isothermal).
- A straight line from B to C (isobaric).
- A straight line from C to A (isochoric).
1. Work Done in Isothermal Process (A to B):
WAB=nRTAln(VBVA)=3RTAln(2)
WBC=PB(VC−VB)=PA2(VA−2VA)=−PAVA2=−3RTA2
WCA=0
Wnet=WAB+WBC+WCA=3RTAln(2)−3RTA2+0
1. Heat Supplied in Isothermal Process (A to B):
QAB=WAB=3RTAln(2)
- Change in Internal Energy:
ΔUBC=nCVΔT=3⋅5R2(TA2−TA)=−15RTA4
- Heat Supplied:
QBC=WBC+ΔUBC=−3RTA2−15RTA4=−21RTA4
QCA=ΔUCA=nCVΔT=3⋅5R2(TA−TA2)=15RTA4
Qnet=QAB+QBC+QCA=3RTAln(2)−21RTA4+15RTA4
Qnet=3RTAln(2)−6RTA4=3RTAln(2)−3RTA2
- Net Work Done:
Wnet=3RTAln(2)−3RTA2
- Net Heat Supplied:
Qnet=3RTAln(2)−3RTA2
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Assertion-Reasoning
6 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Comprehension
56 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Single Correct
140 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
Similar Questions
Three moles of an ideal gas at a pressure PA and temperature TA is isothermally expanded to twice its initial volume. It is then compressed at constant pressure to its original , volume. Finally the gas is compressed at constant volume to its original pressure PA
(a) Sketch the P-V and P-T diagrams for the complete process.
(b) Calculate the net work done by the gas, and net heat supplied to the gas during the complete process.
View SolutionThree moles of an ideal gas (Cp=72R) at pressure p0 and temperature T0 is isothermally expanded to twice its initial volume. It is then compressed at a constant pressure to its original volume.
(a) Sketch p-V and p-T diagram for complete process.
(b) Calculate net work done by the gas.
(c) Calculate net heat supplied to the gas during complete process.
(Write your answer in terms of gas constant =R)
View Solution
Knowledge Check
A mass of ideal gas at pressure P is expanded isothermally to four times the originl volume and then slowly compressed adiabatically to its original volume. Assuming γ to be 1.5 , the new pressure of the gas is
A0.58333333333333BPC0.66666666666667DP/2
A sample of an ideal gas has pressure p0, volume V0 and tempreture T0. It is isothermally expanded to twice its oringinal volume.it is then compressed at constant pressure to have the original volume V0. Finally, the gas is heated at constant volume to get the original tempreture.(a) show the process in a V-T diagram (b) calculate the heat absorbed in the process.
View SolutionAn ideal gas intially has pressure P volume V and temperature T. Its is isothermally expanded to four times of its original volume, then it is compressed at constant pressure to attain its original volume V. Finally, the gas is heated at constant volume to get the original temperature T. (a) Draw V−T curve (b) Calculate the total work done by the gas in the process.(given ln2=0.693)
View SolutionIf a gas is heated at constant pressure, its isothermal compressibility
View SolutionOne mole of an ideal gas at pressure P0 and temperature T0 is expanded isothermally to twice its volume and then compressed at constant pressure to (V0/2) and the gas is brought bac to original state by a process in which PαV (pressure is directly proportional to volume). The correct temperature of the process is
View Solutionn moles of a gas are filled in a container at temperature T. If the gas is slowly and isothermally compressed to half its initial volume, the work done by the atmosphere on the gas is

View SolutionA monoatomic gas at pressure P1 and volume V1 is compressed adiabatically to 18th of its original volume. What is the final pressure of gas.
View SolutionIf a gas of a volume V1 at pressure p1 is compressed adiabatically to volume V2 and pressure p2, calculate the work done by the gas.
View Solution
