a process A rarr D is difficult to occur directly instead it takes place in three successive steps, DeltaS(ArarrB)=40 e.u., DeltaS(BrarrC)=30 e.u., DeltaS(DrarrC)=20 e.u. where e.u. is entropy unit then the entropy change DeltaS for the process (ArarrD) is
+ 90 e.u.
+ 50 e.u.
-90 e.u.
- 50 e.u.
The correct Answer is:B
To calculate the total entropy change (ΔS) for the process A → D, we will add the entropy changes for each of the three successive steps: A → B, B → C, and D → C.
1. Identify the given entropy changes:
- ΔS(A → B) = 40 e.u.
- ΔS(B → C) = 30 e.u.
- ΔS(D → C) = 20 e.u.
2. Recognize the relationship between D and C:
- Since we need to find ΔS(A → D), we can express it in terms of the steps we have:
- ΔS(A → D) = ΔS(A → B) + ΔS(B → C) + ΔS(C → D)
3. Calculate ΔS(C → D):
- The process D → C has an entropy change of +20 e.u.
- Therefore, the reverse process C → D will have an entropy change of:
ΔS(C→D)=−ΔS(D→C)=−20 e.u.
4. Combine all the entropy changes:
- Now we can substitute the values into the equation:
ΔS(A→D)=ΔS(A→B)+ΔS(B→C)+ΔS(C→D)
ΔS(A→D)=40 e.u.+30 e.u.−20 e.u.
5. Perform the calculation:
ΔS(A→D)=40+30−20=50 e.u.
Final Answer:
The total entropy change ΔS for the process A → D is 50 e.u..
---
- ΔS(A → B) = 40 e.u.
- ΔS(B → C) = 30 e.u.
- ΔS(D → C) = 20 e.u.
- Since we need to find ΔS(A → D), we can express it in terms of the steps we have:
- ΔS(A → D) = ΔS(A → B) + ΔS(B → C) + ΔS(C → D)
- The process D → C has an entropy change of +20 e.u.
- Therefore, the reverse process C → D will have an entropy change of:
ΔS(C→D)=−ΔS(D→C)=−20 e.u.
- Now we can substitute the values into the equation:
ΔS(A→D)=ΔS(A→B)+ΔS(B→C)+ΔS(C→D)
ΔS(A→D)=40 e.u.+30 e.u.−20 e.u.
ΔS(A→D)=40+30−20=50 e.u.
The total entropy change ΔS for the process A → D is 50 e.u..
Topper's Solved these Questions
Similar Questions
The direct conversion of A to B is difficult, hence it is carried out as
A→C→D→B
Given, ΔS(A→C)=50eU,ΔS(C→D)=30eU,ΔS(B→D)=20eU, where eU is entropy unit. Thus the change in entropy in (A→B) is:
View SolutionThe direct conversion of A to B is difficult, hence it is carried out as
A→C→D→B
Given, ΔS(A→C)=50eU,ΔS(C→D)=30eU,ΔS(B→D)=20eU, where eU is entropy unit. Thus the change in entropy in (A→B) is:
View SolutionThe direct conversion of A or B is difficult, hence it is carried out by the following shown path
Given, ΔSA→C=50eu, ΔSC→D=30eu,ΔSB→D=20eu
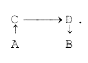
Where eu is entropy unit, then ΔSA→B is .
View SolutionP−V diagram of a cyclic process ABCA is as shown in Fig. Choose the correct alternative

(A)ΔQA→B= negative (B)ΔUB→C= positive (C)ΔUC→A= negative (D)ΔWCAB= negative
View SolutionA reversible heat engine carries 1 mole of an ideal monatomic gas around the cycle 1-2-3-1. Process 1-2 takes place at constant volume, process 2-3 is adiabatic, and process 3-1 takes place at constant pressure. Complete the values for the heat ΔQ, the change in internal energy ΔU, and the work done Δ, for each of the three processes and for the cycle as a whole.

View SolutionDependence of Spontaneity on Temperature:
For a process to be spontaneous , at constant temperature and pressure , there must be decrease in free energy of the system in the direction of the process , i.e. ΔGP.T<0.ΔGP.T=0 implies the equilibrium condition and ΔGP.T>0 corresponds to non- spontaneity.
Gibbs- Helmholtz equation relates the free energy change to the enthalpy and entropy changes of the process as : ΔGP.T=ΔH−TΔS ...(1)
The magnitude of ΔH does not change much with the change in temperature but the entropy factor TΔS change appreciably . Thus, spontaneity of a process depends very much on temperature.
For endothermic process, both ΔH and ΔS are positive . The energy factor, the first factor of equation, opposes the spontaneity whereas entorpy factor favours it. At low temperature the favourable factor TΔS will be small and may be less than ΔH,ΔG will have positive value indicated the nonspontaneity of the process. On raising temperature , the factor TΔS Increases appreciably and when it exceeds ΔH,ΔG would become negative and the process would be spontaneous .
For an expthermic process, both ΔH and ΔS would be negative . In this case the first factor of eq.1 favours the spontaneity whereas the second factor opposes it. At high temperature , when TΔS>ΔH,ΔG will have positive value, showing thereby the non-spontaneity fo the process . However , on decreasing temperature , the factor ,TΔS decreases rapidly and when TΔS<ΔH,ΔG becomes negative and the process occurs spontaneously. Thus , an exothermic process may be spontaneous at low temperature and non-spontaneous at high temperature.
For the reaction at 298K,2A+B→C
ΔH=100kcal and ΔS=0.050kcalK−1. If ΔH and ΔS are assumed to be constant over the temperature range, above what temperature will the reaction become spontaneous?
View SolutionDependence of Spontaneity on Temperature:
For a process to be spontaneous , at constant temperature and pressure , there must be decrease in free energy of the system in the direction of the process , i.e. ΔGP.T<0.ΔGP.T=0 implies the equilibrium condition and ΔGP.T>0 corresponds to non- spontaneity.
Gibbs- Helmholtz equation relates the free energy change to the enthalpy and entropy changes of the process as : ΔGP.T=ΔH−TΔS ...(1)
The magnitude of ΔH does not change much with the change in temperature but the entropy factor TΔS change appreciably . Thus, spontaneity of a process depends very much on temperature.
For endothermic process, both ΔH and ΔS are positive . The energy factor, the first factor of equation, opposes the spontaneity whereas entorpy factor favours it. At low temperature the favourable factor TΔS will be small and may be less than ΔH,ΔG will have positive value indicated the nonspontaneity of the process. On raising temperature , the factor TΔS Increases appreciably and when it exceeds ΔH,ΔG would become negative and the process would be spontaneous .
For an expthermic process, both ΔH and ΔS would be negative . In this case the first factor of eq.1 favours the spontaneity whereas the second factor opposes it. At high temperature , when TΔS>ΔH,ΔG will have positive value, showing thereby the non-spontaneity fo the process . However , on decreasing temperature , the factor ,TΔS decreases rapidly and when TΔS<ΔH,ΔG becomes negative and the process occurs spontaneously. Thus , an exothermic process may be spontaneous at low temperature and non-spontaneous at high temperature.
For the reaction at 25∘,X2O4(l)→2XO2(g)
ΔH=2.1Kcal and ΔS=20calK−1. The reaction would be
View SolutionDependence of Spontaneity on Temperature:
For a process to be spontaneous , at constant temperature and pressure , there must be decrease in free energy of the system in the direction of the process , i.e. ΔGP.T<0.ΔGP.T=0 implies the equilibrium condition and ΔGP.T>0 corresponds to non- spontaneity.
Gibbs- Helmholtz equation relates the free energy change to the enthalpy and entropy changes of the process as : ΔGP.T=ΔH−TΔS ...(1)
The magnitude of ΔH does not change much with the change in temperature but the entropy factor TΔS change appreciably . Thus, spontaneity of a process depends very much on temperature.
For endothermic process, both ΔH and ΔS are positive . The energy factor, the first factor of equation, opposes the spontaneity whereas entorpy factor favours it. At low temperature the favourable factor TΔS will be small and may be less than ΔH,ΔG will have positive value indicated the nonspontaneity of the process. On raising temperature , the factor TΔS Increases appreciably and when it exceeds ΔH,ΔG would become negative and the process would be spontaneous .
For an expthermic process, both ΔH and ΔS would be negative . In this case the first factor of eq.1 favours the spontaneity whereas the second factor opposes it. At high temperature , when TΔS>ΔH,ΔG will have positive value, showing thereby the non-spontaneity fo the process . However , on decreasing temperature , the factor ,TΔS decreases rapidly and when TΔS<ΔH,ΔG becomes negative and the process occurs spontaneously. Thus , an exothermic process may be spontaneous at low temperature and non-spontaneous at high temperature.
A reaction has a value of ΔH=−40Kcal at 400 k cal mol−1. The reaction is spontaneous, below this temperature , it is not . The values fo ΔG and ΔS at 400 k are respectively
View SolutionDependence of Spontaneity on Temperature:
For a process to be spontaneous , at constant temperature and pressure , there must be decrease in free energy of the system in the direction of the process , i.e. ΔGP.T<0.ΔGP.T=0 implies the equilibrium condition and ΔGP.T>0 corresponds to non- spontaneity.
Gibbs- Helmholtz equation relates the free energy change to the enthalpy and entropy changes of the process as : ΔGP.T=ΔH−TΔS ...(1)
The magnitude of ΔH does not change much with the change in temperature but the entropy factor TΔS change appreciably . Thus, spontaneity of a process depends very much on temperature.
For endothermic process, both ΔH and ΔS are positive . The energy factor, the first factor of equation, opposes the spontaneity whereas entorpy factor favours it. At low temperature the favourable factor TΔS will be small and may be less than ΔH,ΔG will have positive value indicated the nonspontaneity of the process. On raising temperature , the factor TΔS Increases appreciably and when it exceeds ΔH,ΔG would become negative and the process would be spontaneous .
For an expthermic process, both ΔH and ΔS would be negative . In this case the first factor of eq.1 favours the spontaneity whereas the second factor opposes it. At high temperature , when TΔS>ΔH,ΔG will have positive value, showing thereby the non-spontaneity fo the process . However , on decreasing temperature , the factor ,TΔS decreases rapidly and when TΔS<ΔH,ΔG becomes negative and the process occurs spontaneously. Thus , an exothermic process may be spontaneous at low temperature and non-spontaneous at high temperature.
When CaCO3 is heated to a high temperature , it undergoes decomposition into CaO and CO2 whereas it is quite stable at room temperature . The most likely explanation of it, is
View SolutionAs per second law of thermodynamics a process taken place spontaneously if and only if the entropy of the universe increases due to the process. Change in entropy is given by
ΔS=QrevT
What is the change in entropy of the universe due to the following reaction occuring at 27∘C ?
A+2B→C+2D,ΔH=+1.8kJmol−1
Molar entropy values of A, B, C and D are 1,2,3 and 4JK−1mol−1 respectively.
View Solution
