The direct conversion of A to B is difficult, hence it is carried out as
A→C→D→B
Given, ΔS(A→C)=50eU,ΔS(C→D)=30eU,ΔS(B→D)=20eU, where eU is entropy unit. Thus the change in entropy in (A→B) is:
100eU
60eU
−100eU
−60eU
To find the change in entropy from A to B, we can use the provided values of entropy changes for the intermediate steps. The process is as follows:
1. Identify the given entropy changes:
- ΔSA→C=50eU
- ΔSC→D=30eU
- ΔSB→D=20eU
2. Express the changes in terms of entropy:
- From the first step, we can express the change in entropy from A to C as:
ΔSA→C=SC−SA
- From the second step, the change in entropy from C to D is:
ΔSC→D=SD−SC
- From the third step, the change in entropy from B to D is:
ΔSB→D=SD−SB
3. Calculate the total change in entropy from A to B:
- We need to find ΔSA→B, which can be expressed as:
ΔSA→B=SB−SA
- To find this, we can combine the equations:
ΔSA→B=(SD−SB)+(SC−SA)+(SD−SC)
- Rearranging gives:
ΔSA→B=(SC−SA)+(SD−SC)−(SD−SB)
- This simplifies to:
ΔSA→B=(SC−SA)+(SB−SD)
4. Substituting the known values:
- From the values given:
ΔSA→B=50+30−20
- Calculating this gives:
ΔSA→B=60eU
5. Conclusion:
- Therefore, the change in entropy from A to B is 60eU.
Final Answer:
The change in entropy from A to B is 60eU.
- ΔSA→C=50eU
- ΔSC→D=30eU
- ΔSB→D=20eU
- From the first step, we can express the change in entropy from A to C as:
ΔSA→C=SC−SA
- From the second step, the change in entropy from C to D is:
ΔSC→D=SD−SC
- From the third step, the change in entropy from B to D is:
ΔSB→D=SD−SB
- We need to find ΔSA→B, which can be expressed as:
ΔSA→B=SB−SA
- To find this, we can combine the equations:
ΔSA→B=(SD−SB)+(SC−SA)+(SD−SC)
- Rearranging gives:
ΔSA→B=(SC−SA)+(SD−SC)−(SD−SB)
- This simplifies to:
ΔSA→B=(SC−SA)+(SB−SD)
- From the values given:
ΔSA→B=50+30−20
- Calculating this gives:
ΔSA→B=60eU
- Therefore, the change in entropy from A to B is 60eU.
The change in entropy from A to B is 60eU.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercise
1 Videos
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Ex 6.1
26 Videos
- STOICHIOMETRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STOICHIOMETRYEXERCISE - Archives Subjective
33 Videos
Similar Questions
The direct conversion of A or B is difficult, hence it is carried out by the following shown path
Given, ΔSA→C=50eu, ΔSC→D=30eu,ΔSB→D=20eu
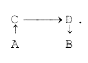
Where eu is entropy unit, then ΔSA→B is .
View Solutiona process A rarr D is difficult to occur directly instead it takes place in three successive steps, DeltaS(ArarrB)=40 e.u., DeltaS(BrarrC)=30 e.u., DeltaS(DrarrC)=20 e.u. where e.u. is entropy unit then the entropy change DeltaS for the process (ArarrD) is
View SolutionAs per second law of thermodynamics a process taken place spontaneously if and only if the entropy of the universe increases due to the process. Change in entropy is given by
ΔS=QrevT
What is the change in entropy of the universe due to the following reaction occuring at 27∘C ?
A+2B→C+2D,ΔH=+1.8kJmol−1
Molar entropy values of A, B, C and D are 1,2,3 and 4JK−1mol−1 respectively.
View SolutionA gaseous reactant A forms two different product, in parallel reaction , B and C as follows:
A→B,ΔH∘=−3KJ,ΔS∘=20JK−1 , A→C,ΔH∘=−3.6KJ,ΔS∘=10JK−1
Discuss the relative stability of B and C on the basis of Gibb's free energy change at 27∘C.
View SolutionFor a sponaneous reaction, the free energy change must be negative, ΔG=ΔH−TΔS,ΔH is the enthalpy change during the reaction. T is the absolute temperature, and ΔS is the change in entropy during the reaction. Consider a reaction such as the formation of an oxide
M+O2→MO
Dioxygen is used up in the course of this reaction. Gases have a more random structure (less ordered) than liquid or solids. Consequently gases have a higher entropy than liquids and solids. In this reaction S (entropy or randomness) decreases, hence ΔS is negative. Thus, if the temperature is raised then TΔS becomes more negative,Since, TΔS is substracted in the equation, then ΔG becomes less negative. Thus, the free energy change increases with the increase in temperature.
The free energy changes that occur when one mole of common reactant (in this case dioxygen) is used may be plotted graphically aginst temperature for a number of reactions of metals to their oxides. The following plot is called an Ellingham diagram for metal oxide. Understanding of Ellingham diagram is extremely important for the efficient extraction of metals.
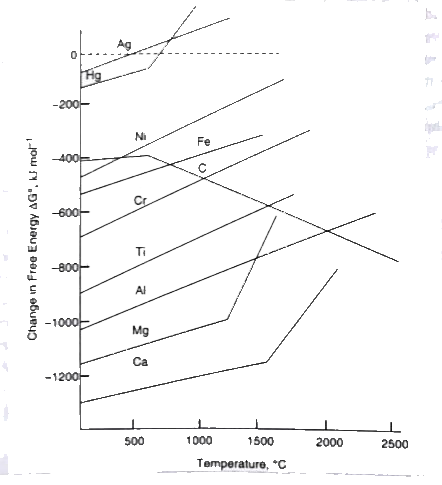
Which of the following elements can be prepared by heating the oxide above 400∘C ?
View SolutionFree energy, G=H-TS, is a state function that includes whether a reaction is spontaneous or non-spontaneous. If you think of TS as the part of the system's energy that is disordered already, then (H-TS) is the part of the system's energy that is still ordered and therefore free to cause spontaneous change by becoming disordered.
Also, ΔG=ΔH−TΔS
To see what this equation for free energy change has to do with spontaneity let us return to relationship.
ΔStotal=ΔSsys+ΔSsurr=ΔS+ΔSsurr
(It is generally understood that symbols without subscript refer to the system not the surroundings.)
ΔSsurr=−ΔHT, where ΔH is the heat gained by then system at constant pressure.
ΔStotal=ΔS−ΔHT
⇒TΔHtotal=ΔH−TΔS
⇒−TΔStotal=ΔH−TΔS
i.e. ΔG=−TΔStotal
From second law of thermodynamics, a reaction is spontaneous if ΔStotal is positive, non-spontanous if ΔStotal is negative and at equilibrium if ΔStotal is zero.
Since, −TΔS=ΔG and since ΔG and ΔS have opposite signs, we can restate the thermodynamic criterion for the spontaneity of a reaction carried out at constant temperature and pressure.
If ΔG<0, the reaction is spontaneous.
If ΔG>0, the reaction is non-spontanous.
If ΔG=0, the reaction is at equilibrium.
In the equation, ΔG=ΔH−TΔS, temperature is a weighting factor that determine the relative importance of enthalpy contribution to ΔG.
Read the above paragraph carefully and answer the following questions based on above comprehension:
One mole of ice is converted to liquid at 273 K, H2O(s) and H2O(l) have entropies 38.20 and 60.03 J mol−1K−1. Enthalpy change in the conversion will be:
View SolutionFree energy, G=H-TS, is a state function that includes whether a reaction is spontaneous or non-spontaneous. If you think of TS as the part of the system's energy that is disordered already, then (H-TS) is the part of the system's energy that is still ordered and therefore free to cause spontaneous change by becoming disordered.
Also, ΔG=ΔH−TΔS
To see what this equation for free energy change has to do with spontaneity let us return to relationship.
ΔStotal=ΔSsys+ΔSsurr=ΔS+ΔSsurr
(It is generally understood that symbols without subscript refer to the system not the surroundings.)
ΔSsurr=−ΔHT, where ΔH is the heat gained by then system at constant pressure.
ΔStotal=ΔS−ΔHT
⇒TΔHtotal=ΔH−TΔS
⇒−TΔStotal=ΔH−TΔS
i.e. ΔG=−TΔStotal
From second law of thermodynamics, a reaction is spontaneous if ΔStotal is positive, non-spontanous if ΔStotal is negative and at equilibrium if ΔStotal is zero.
Since, −TΔS=ΔG and since ΔG and ΔS have opposite signs, we can restate the thermodynamic criterion for the spontaneity of a reaction carried out at constant temperature and pressure.
If ΔG<0, the reaction is spontaneous.
If ΔG>0, the reaction is non-spontanous.
If ΔG=0, the reaction is at equilibrium.
In the equation, ΔG=ΔH−TΔS, temperature is a weighting factor that determine the relative importance of enthalpy contribution to ΔG.
Read the above paragraph carefully and answer the following questions based on above comprehension:
Which of the following is true for the reaction?
H2O(l) H2O(g) at 100∘ C and 1 atmosphere?
View SolutionEntropy is a state function and its value depends on two or three variable temperature (T), Pressure(P) and volume (V). Entropy change for an ideal gas having number of moles(n) can be determined by the following equation.
ΔS=2.303nCvlog(T2T1)+2.303nR log(V2V1)
ΔS=2.303nCPlog(T2T1)+2.303nR log(P1P2)
Since free energy change for a process or a chemical equation is a deciding factor of spontaneity , which can be obtained by using entropy change (ΔS) according to the expression, ΔG=ΔH−TΔS at a temperature T
What would be the entropy change involved in thermodynamic expansion of 2 moles of a gas from a volume of 5 L to a volume of 50 L at 25∘ C [Given R=8.3J/mole−K]
View SolutionThe P−V diagram of a system undergoing thermodynnaic transformation is shown in Fig. The work done on the system in going from A→B→C is 50J and 20cal heat is given to the system. The change in internal erergy between A and C is

View SolutionGibbs-Helmoholtz equation relates the free energy change to the enthalpy and entropy changes of the process as
(ΔG)PT=ΔH−TΔS
The magnitude of ΔH does not change much with the change in temperature but the enrgy factor TΔS changes appreciably. Thus, spontaneity of a process depends very much on temperature.
For the reaction at 298K,2A+B→C
ΔH=100kcal and ΔS=0.020kcalK−1. If ΔH and ΔS are assumed to be constant over the temperature range, at what temperature will the reaction become spontaneous?
View Solution
