83Bi2H(t12=130sec) decays to 81Tl207 by α-emission. In an experiment starting with 5 moles of 83Bi211. how much pressure would be developed in a 350 L closed vessel at 25 C after 760 sec? [Antilog (1.759) = 57 41]
0.68 atm
0.22 atm
0.34 atm
0.54 atm
The correct Answer is:C
To solve the problem, we will follow these steps:
Step 1: Understand the decay process
The decay process is given as:
21183Bi→20781Tl+42He
This indicates that Bismuth-211 decays to Thallium-207 and emits an alpha particle (Helium-4).
Step 2: Determine the decay constant (k)
The half-life (t1/2) of Bismuth-211 is given as 130 seconds. The decay constant (k) can be calculated using the formula:
k=ln(2)t1/2
Substituting the values:
k=0.693130≈0.005338s−1
Step 3: Calculate the number of moles of Bismuth remaining after 760 seconds
Using the formula for radioactive decay:
N=N0e−kt
Where:
- N0 = initial number of moles of Bismuth = 5 moles
- k = decay constant = 0.005338 s−1
- t = time = 760 seconds
Calculating N:
N=5e−0.005338×760
Calculating the exponent:
−kt=−0.005338×760≈−4.05288
Now, calculating e−4.05288:
N≈5×e−4.05288≈5×0.0176≈0.088
Thus, the remaining moles of Bismuth:
N≈5−0.088≈4.912
Step 4: Calculate the number of moles of Thallium produced
Since each decay of Bismuth produces one mole of Thallium:
Moles of Tl=0.088
Step 5: Calculate the pressure in the closed vessel
Using the ideal gas law:
PV=nRT
Where:
- P = pressure (atm)
- V = volume (350 L)
- n = moles of gas (remaining Bismuth)
- R = ideal gas constant = 0.0821 L·atm/(K·mol)
- T = temperature in Kelvin = 25°C = 298 K
Substituting the values:
P×350=4.912×0.0821×298
Calculating the right side:
P×350=120.052
Now solving for P:
P=120.052350≈0.343
Final Answer
The pressure developed in the closed vessel after 760 seconds is approximately:
P≈0.34atm
The decay process is given as:
21183Bi→20781Tl+42He
This indicates that Bismuth-211 decays to Thallium-207 and emits an alpha particle (Helium-4).
The half-life (t1/2) of Bismuth-211 is given as 130 seconds. The decay constant (k) can be calculated using the formula:
k=ln(2)t1/2
Substituting the values:
k=0.693130≈0.005338s−1
Using the formula for radioactive decay:
N=N0e−kt
Where:
- N0 = initial number of moles of Bismuth = 5 moles
- k = decay constant = 0.005338 s−1
- t = time = 760 seconds
N=5e−0.005338×760
Calculating the exponent:
−kt=−0.005338×760≈−4.05288
Now, calculating e−4.05288:
N≈5×e−4.05288≈5×0.0176≈0.088
Thus, the remaining moles of Bismuth:
N≈5−0.088≈4.912
Since each decay of Bismuth produces one mole of Thallium:
Moles of Tl=0.088
Using the ideal gas law:
PV=nRT
Where:
- P = pressure (atm)
- V = volume (350 L)
- n = moles of gas (remaining Bismuth)
- R = ideal gas constant = 0.0821 L·atm/(K·mol)
- T = temperature in Kelvin = 25°C = 298 K
P×350=4.912×0.0821×298
Calculating the right side:
P×350=120.052
Now solving for P:
P=120.052350≈0.343
The pressure developed in the closed vessel after 760 seconds is approximately:
P≈0.34atm
Topper's Solved these Questions
- MOCK_TEST_17BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOCK_TEST_17EXERCISE - Example
23 Videos
- ORGANIC CHEMISTRY : SOME BASIC PRINCIPLES AND TECHNIQUES BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ORGANIC CHEMISTRY : SOME BASIC PRINCIPLES AND TECHNIQUES EXERCISE - Assignment(Section-D)(Assertion - Reason Type Questions)
15 Videos
Similar Questions
.21884Po(t1/2=183 sec) decay to .82Pb(t1/2=161 sec) by α-emission, while Pb214 is a β-emitter. In an experiment starting with 1 mole of pure Po218, how many time would be required for the number of nuclei of .21482Pb to reach maximum ?
View Solution.84Po218(t1/2=3.05min) decays to .82Pb214(t1/2=2.68min) by α emisison while Pb214 is β-emitter. In an experiment starting with 1g atom of pure Po218, how much time would be required for the concentration of Pb214 to reach maximum?
View SolutionThe radioactive decay .21183Bi→20781Ti , takes place in 100L closed vessel at 27∘C Starting with 2 mols of _(83)211Bi(t1/2=130sec) , the presuure development in the vessel after 520 sec will be:
View SolutionAt 27∘C, hydrogen is leaked through a tiny hole into a vessel for 20min. Another unknown gas at the same T and P as that of H2, is leaked through the same hole for 20 min. After the effusion of the gases the mixture exerts a pressure of 6 atm. The hydrogen content of the mixture is 0.7 mole. If the volume of the container is 3 litre, what is molecular weight of unknown gas ?
(Use:R=0.821L atm K−1mole−1)
View SolutionEntropy is a state function and its value depends on two or three variable temperature (T), Pressure(P) and volume (V). Entropy change for an ideal gas having number of moles(n) can be determined by the following equation.
ΔS=2.303nCvlog(T2T1)+2.303nR log(V2V1)
ΔS=2.303nCPlog(T2T1)+2.303nR log(P1P2)
Since free energy change for a process or a chemical equation is a deciding factor of spontaneity , which can be obtained by using entropy change (ΔS) according to the expression, ΔG=ΔH−TΔS at a temperature T
What would be the entropy change involved in thermodynamic expansion of 2 moles of a gas from a volume of 5 L to a volume of 50 L at 25∘ C [Given R=8.3J/mole−K]
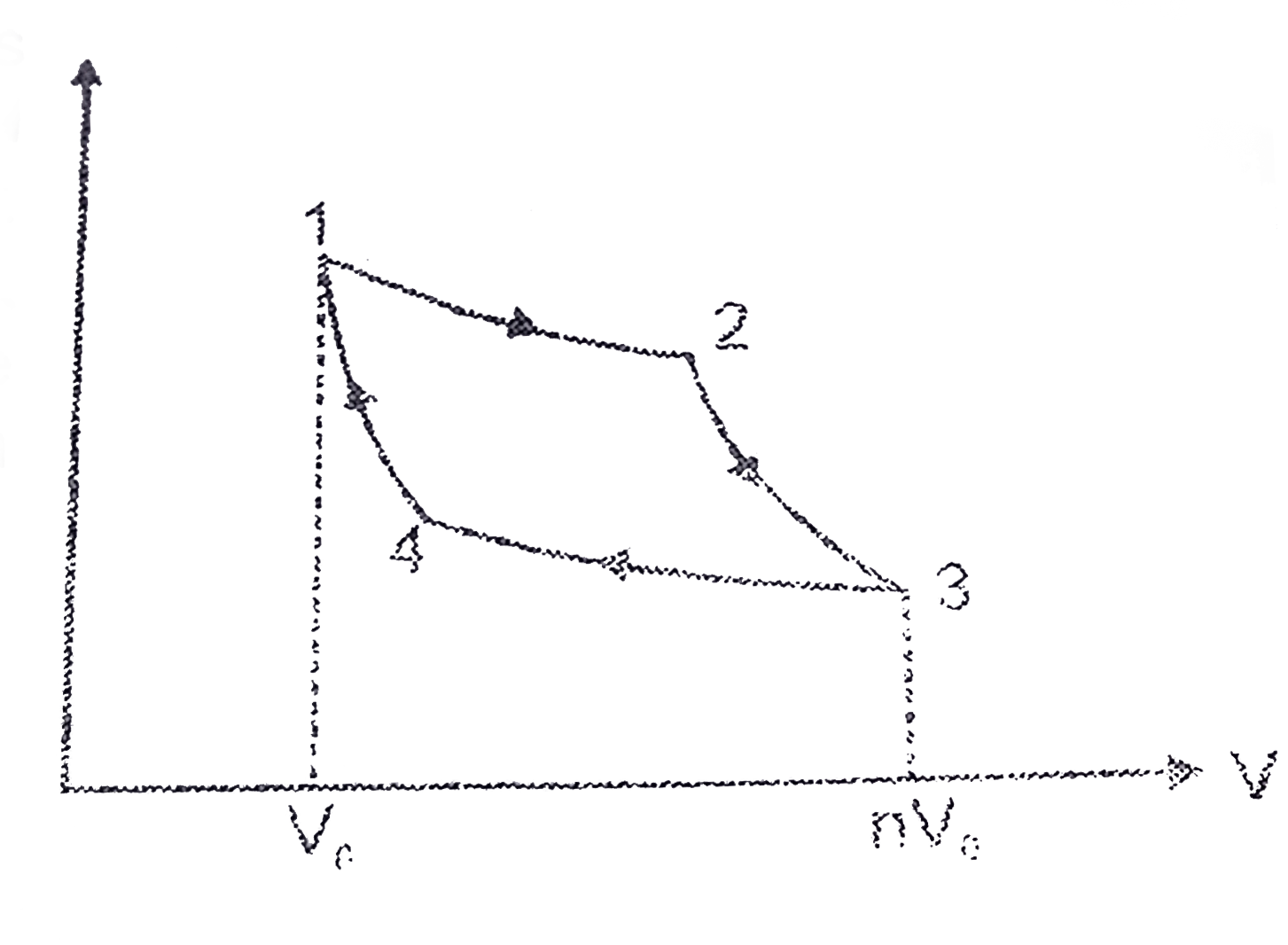
View SolutionA Carnot engine cycle is shown in the Fig. (2). The cycle runs between temperatures TH=αTL=T0(α>T). Minimum and maximum volume at state 1 and states 3 are V0 and nV0 respectively. The cycle uses one mole of an ideal gas with CP/CV=γ. Here CP and CV are the specific heats at constant pressure and volume respectively. You must express all answers in terms of the given parameters {α,n,T0,V0?} and universal gas constant R.
(a) Find P,V,T for all the states
(b) Calculate the work done by the engine in each process: W12,W23,W34,W41.
(c) Calculate Q, the heat absorbed in the cycle.
View SolutionThe mass of a nucleus .AZX is less that the sum of the masses of (A−Z) number of neutrons and Z number of protons in the nucleus.The energy equivalent to the corresponding mass difference is known as the binding energy of the nucleus. A heavy nucleus of mass M can break into two light nuclei of masses m1 and m2 only if (m1+m2)<M. Also two light nuclei of masses m3 and m4 can undergo complete fusion and form a heavy nucleus of mass M'. only if (m3+m4)>M'. The masses of some neutral atoms are given in the table below:
∣∣ ∣ ∣∣.11H1.007825u.21H2.014102u.31H3.016050u.42He4.002603u.63Li6.015123u.73Li7.016004u.7030Zn69.925325u.8234Se81.916709u.15264Gd151.91980u.20682Pb205.974455u.20983Bi208.980388u.21084Po209.982876u∣∣ ∣ ∣∣
Taking kinetic energy ( in KeV) of the alpha particle, when the nucleus .21084P0 at rest undergoes alpha decay, is:
View Solution
