Two balls each of mass 2kg (one at rest) undergo oblique collision is perfectly elastic, then the angle between their velocities after collision is
30°
60°
45°
90°
The correct Answer is:D
To solve the problem of two balls undergoing a perfectly elastic oblique collision, we will follow these steps:
Step 1: Understand the Collision
We have two balls, each with a mass of 2 kg. One ball is moving while the other is at rest. Since the collision is perfectly elastic, both momentum and kinetic energy will be conserved.
Step 2: Define the Initial Conditions
Let’s denote:
- Ball 1 (moving) has an initial velocity →u1 (let's say it moves along the x-axis).
- Ball 2 (at rest) has an initial velocity →u2=0.
Step 3: Apply Conservation of Momentum
In an elastic collision, the total momentum before and after the collision must be equal. The momentum conservation equation can be written as:
m1→u1+m2→u2=m1→v1+m2→v2
Since both balls have the same mass (2 kg), we can simplify this equation.
Step 4: Analyze the Velocities After Collision
After the collision, let:
- Ball 1 moves at an angle θ with velocity →v1.
- Ball 2 moves at an angle ϕ with velocity →v2.
Step 5: Use the Coefficient of Restitution
For perfectly elastic collisions, the coefficient of restitution e=1. The equation for the coefficient of restitution along the line of impact can be expressed as:
e=|→v2−→v1||→u1−→u2|
Since →u2=0, this simplifies to:
1=|→v2−→v1||→u1|
Step 6: Determine the Angle Between Their Velocities
In a perfectly elastic collision between two equal masses, the two balls will move off at right angles to each other after the collision. This means that the angle θ between their velocities after the collision is 90∘.
Conclusion
Thus, the angle between the velocities of the two balls after the collision is 90∘.
We have two balls, each with a mass of 2 kg. One ball is moving while the other is at rest. Since the collision is perfectly elastic, both momentum and kinetic energy will be conserved.
Let’s denote:
- Ball 1 (moving) has an initial velocity →u1 (let's say it moves along the x-axis).
- Ball 2 (at rest) has an initial velocity →u2=0.
In an elastic collision, the total momentum before and after the collision must be equal. The momentum conservation equation can be written as:
m1→u1+m2→u2=m1→v1+m2→v2
Since both balls have the same mass (2 kg), we can simplify this equation.
After the collision, let:
- Ball 1 moves at an angle θ with velocity →v1.
- Ball 2 moves at an angle ϕ with velocity →v2.
For perfectly elastic collisions, the coefficient of restitution e=1. The equation for the coefficient of restitution along the line of impact can be expressed as:
e=|→v2−→v1||→u1−→u2|
Since →u2=0, this simplifies to:
1=|→v2−→v1||→u1|
In a perfectly elastic collision between two equal masses, the two balls will move off at right angles to each other after the collision. This means that the angle θ between their velocities after the collision is 90∘.
Thus, the angle between the velocities of the two balls after the collision is 90∘.
Topper's Solved these Questions
Similar Questions
Two balls of equal masses m each undergo oblique collision. If colision is perfectly elastic, then angle between their velocities after collision is
View SolutionBlock A has a mass 3kg and is sliding on a rough horizontal surface with a velocity uA=2m/s when it makes a direct collision with block B, which has a mass of 2kg and is originally at rest. The collision is perfectly elastic. Determine the velocity of each block just after collision and the distance between the blocks when they stop sliding. The coefficient of kinetic friction between the blocks and the plane is μk=0.3 ( Take g=10m/s2)
View Solution
Knowledge Check
Two objects, one of mass 3 kg and moving with speed of 2 m/s and the other of mass 5 kg and speed 2 m/s, move toward each other and collide head-on. If the collision is perfectly inelastic, find the speed of the object after the collision.
A0.25m/sB0.5m/sC0.75m/sD1m/s
Two balls roll toward each other. The red ball has a mass of 0.5 kg and a speed of 4m/s just before impact. The green ball has a mass of 0.3 kg and a speed of 2 m/s. if the collision is perfectly inelastic, determine the velocity of the composite object after the collision.
View SolutionTwo balls of masses m and 2m moving in opposite directions collide head on elastically with velocities v and 2v. Find their velocities after collision.
View SolutionTwo balls of masses m and 2m moving in opposite directions collide head on elastically with velocities v and 2v. Find their velocities after collision.
View Solution(b) Two balls each of mass m moving in opposite direction with equal speed v collide head -on with each other . Predict the outcome of the collision assuming it perfectly elastic.
View SolutionA body (solid sphere) of mass m makes an elastic collision with another idential body at rest. Just after collision the angle between the velocity vector of one body with the initial line of motion is 15∘ then the angle between velocity vector of the other body with the initial line of motion is
View SolutionA ball of mass m is dropped onto a smooth fixed wedge of inclination θ The collision is perfectly elastic . If after the collision, the x component of the velocity of the block is √2gh , then θ is
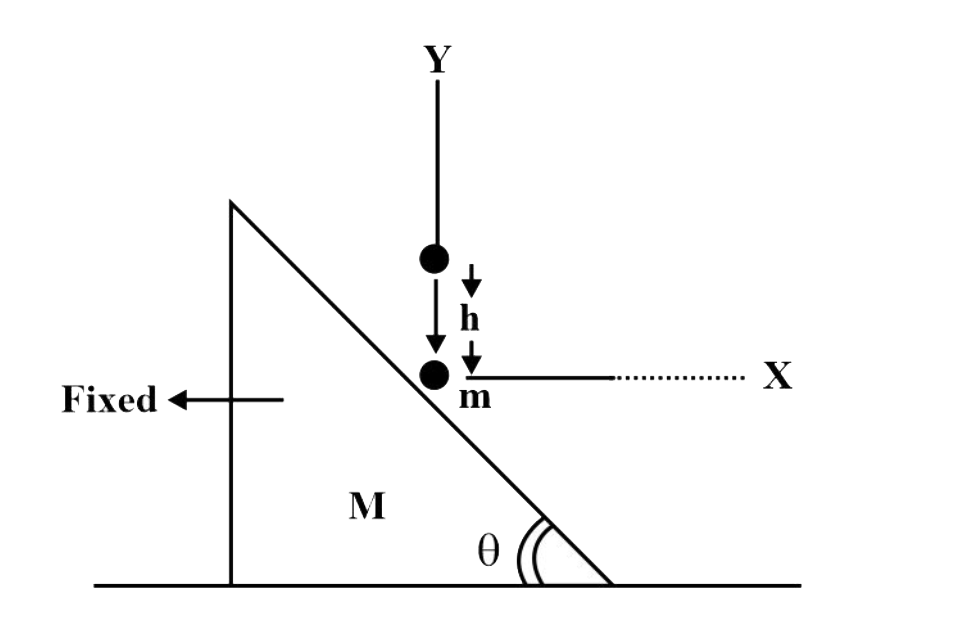
View SolutionAn object is moving towards a mirror with a velocity of 10ms−1 as shown in the figure. If the collision between the mirror and the object is perfectly elastic, then the velocity of the image after collision with mirror in vector form is
View Solution
