A lead sphere is dropped into a medium. As the sphere falls, the velocity of lead sphere
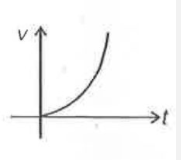

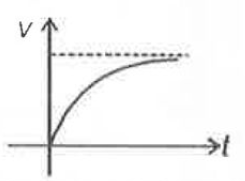
The correct Answer is:D
To solve the problem of a lead sphere falling into a medium, we need to analyze the forces acting on the sphere and how they affect its motion. Here’s a step-by-step breakdown of the solution:
Step 1: Identify the Forces Acting on the Sphere
When the lead sphere is dropped into the medium, three main forces act on it:
1. Gravitational Force (Weight): This force acts downward and is given by Fg=mg, where m is the mass of the sphere and g is the acceleration due to gravity.
2. Buoyant Force: This force acts upward and is equal to the weight of the fluid displaced by the sphere. It is given by Archimedes' principle as Fb=ρfluidVsphereg, where ρfluid is the density of the fluid and Vsphere is the volume of the sphere.
3. Drag Force: As the sphere falls, it experiences a drag force that opposes its motion. This force depends on the velocity of the sphere and is typically modeled as Fd=−kv, where k is a constant that depends on the properties of the fluid and v is the velocity of the sphere.
Step 2: Write the Equation of Motion
The net force acting on the sphere can be expressed as:
Fnet=Fg−Fb−Fd
Using Newton's second law, we can write:
ma=mg−ρfluidVsphereg−kv
where a is the acceleration of the sphere.
Step 3: Analyze the Motion Over Time
Initially, when the sphere is dropped, it will accelerate downwards due to the gravitational force being greater than the sum of the buoyant force and the drag force. As the sphere gains velocity, the drag force increases, which reduces the net force acting on the sphere.
Step 4: Determine Terminal Velocity
Eventually, the sphere will reach a point where the net force becomes zero, meaning the acceleration will be zero. This occurs when:
mg−ρfluidVsphereg−kvterminal=0
At this point, the sphere falls with a constant velocity known as the terminal velocity vterminal.
Step 5: Conclusion
The velocity of the lead sphere will initially increase as it falls, but as the drag force increases, the acceleration will decrease until it reaches zero. At this point, the sphere will continue to fall at a constant terminal velocity.
Final Answer
The velocity of the lead sphere first increases and then becomes constant as it reaches terminal velocity.
---
When the lead sphere is dropped into the medium, three main forces act on it:
1. Gravitational Force (Weight): This force acts downward and is given by Fg=mg, where m is the mass of the sphere and g is the acceleration due to gravity.
2. Buoyant Force: This force acts upward and is equal to the weight of the fluid displaced by the sphere. It is given by Archimedes' principle as Fb=ρfluidVsphereg, where ρfluid is the density of the fluid and Vsphere is the volume of the sphere.
3. Drag Force: As the sphere falls, it experiences a drag force that opposes its motion. This force depends on the velocity of the sphere and is typically modeled as Fd=−kv, where k is a constant that depends on the properties of the fluid and v is the velocity of the sphere.
The net force acting on the sphere can be expressed as:
Fnet=Fg−Fb−Fd
Using Newton's second law, we can write:
ma=mg−ρfluidVsphereg−kv
where a is the acceleration of the sphere.
Initially, when the sphere is dropped, it will accelerate downwards due to the gravitational force being greater than the sum of the buoyant force and the drag force. As the sphere gains velocity, the drag force increases, which reduces the net force acting on the sphere.
Eventually, the sphere will reach a point where the net force becomes zero, meaning the acceleration will be zero. This occurs when:
mg−ρfluidVsphereg−kvterminal=0
At this point, the sphere falls with a constant velocity known as the terminal velocity vterminal.
The velocity of the lead sphere will initially increase as it falls, but as the drag force increases, the acceleration will decrease until it reaches zero. At this point, the sphere will continue to fall at a constant terminal velocity.
The velocity of the lead sphere first increases and then becomes constant as it reaches terminal velocity.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A sphere P of mass m and velocity vi undergoes an oblique and perfectly elastic collision with an identical sphere Q initially at rest. The angle θ between the velocities of the spheres after the collision shall be
A0B45∘C90∘D180∘
If the radius of a sphere is doubled, what is the ratio of the volume of the first sphere to that of the second sphere?
View SolutionA sphere of mass m moving with velocity v collides head-on with another sphere of the same mass at rest. If the coefficient of resistitution e=1/2, then what is the ratio of final velocity of the second sphere to the intial velocity of the first sphere ?
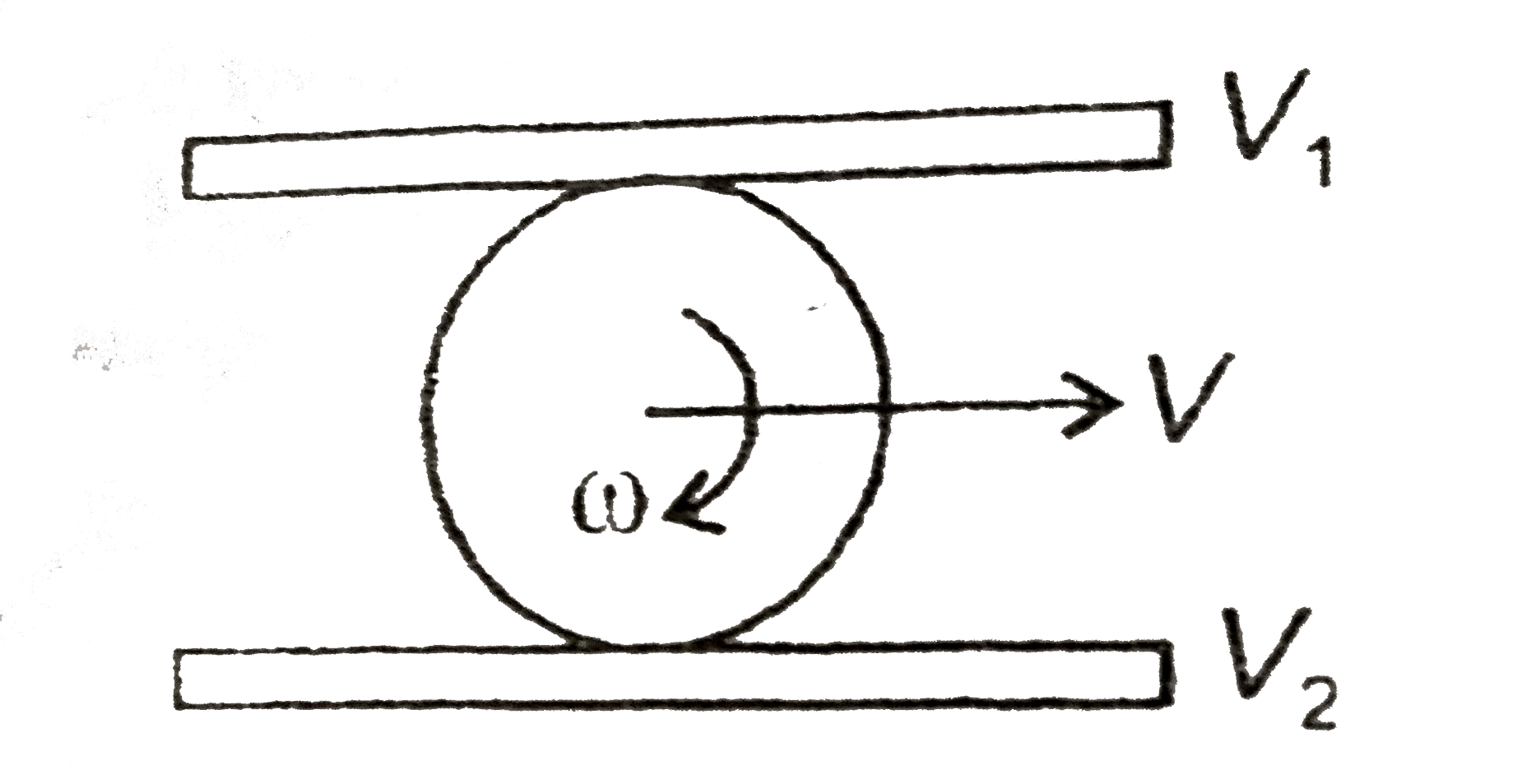
View SolutionA sphere of radius R rolls without slipping between two planks as shown in figure. Find
(a) Speed of centre of sphere
(b) Angular velocity of the sphere
View SolutionA sphere has to purely roll upwards. At an instant when the velocity of sphere is v, frictional force acting on it is

View SolutionA solid sphere is rolling without slipping on rough ground as shown in figure. If collides elastically with an identical another sphere at rest. There is no friction between the two spheres . Radius of each sphere is R and mass is m.
Linear velocity of first sphere after it again starts rolling without slipping is
View SolutionA solid sphere, of radius R acquires a terminal velocity v1 when falling (due to gravity) through a viscous fluid having a coefficient of viscosity η. The sphere is broken into 27 identical solid spheres. If each of these spheres acquires a terminal velocity, v2, when falling through the same fluid, the ratio (v1/v2) equals :
View SolutionA solid sphere, of radius R acquires a terminal velocity v1 when falling (due to gravity) through a viscous fluid having a coefficient of viscosity η he sphere is broken into 27 identical solid spheres. If each of these spheres acquires a terminal velocity v2 when falling through the same fluid, the ratio (v1/v2) equals:
View Solution
