The average value of cos2(ϕ2) in one cycle is
Zero
13
12
14
The correct Answer is:C
To find the average value of cos2(ϕ2) over one complete cycle (from 0 to 2π), we can follow these steps:
Step 1: Set up the formula for average value
The average value A of a function f(ϕ) over the interval (a,b) is given by:
A=1b−a∫baf(ϕ)dϕ
In our case, f(ϕ)=cos2(ϕ2), and we will integrate from 0 to 2π.
Step 2: Write the integral
Thus, the average value becomes:
A=12π−0∫2π0cos2(ϕ2)dϕ
This simplifies to:
A=12π∫2π0cos2(ϕ2)dϕ
Step 3: Use the trigonometric identity
We can use the trigonometric identity:
cos2x=1+cos(2x)2
Applying this identity, we have:
cos2(ϕ2)=1+cos(ϕ)2
Step 4: Substitute the identity into the integral
Now substituting this into the integral:
A=12π∫2π01+cos(ϕ)2dϕ
This simplifies to:
A=14π∫2π0(1+cos(ϕ))dϕ
Step 5: Split the integral
We can split the integral into two parts:
A=14π(∫2π01dϕ+∫2π0cos(ϕ)dϕ)
Step 6: Evaluate the integrals
1. The first integral:
∫2π01dϕ=2π
2. The second integral:
∫2π0cos(ϕ)dϕ=0
(since the integral of cosine over one complete cycle is zero).
Step 7: Substitute back into the average formula
Now substituting these values back:
A=14π(2π+0)=2π4π=12
Final Answer
Thus, the average value of cos2(ϕ2) over one cycle is:
12
The average value A of a function f(ϕ) over the interval (a,b) is given by:
A=1b−a∫baf(ϕ)dϕ
In our case, f(ϕ)=cos2(ϕ2), and we will integrate from 0 to 2π.
Thus, the average value becomes:
A=12π−0∫2π0cos2(ϕ2)dϕ
This simplifies to:
A=12π∫2π0cos2(ϕ2)dϕ
We can use the trigonometric identity:
cos2x=1+cos(2x)2
Applying this identity, we have:
cos2(ϕ2)=1+cos(ϕ)2
Now substituting this into the integral:
A=12π∫2π01+cos(ϕ)2dϕ
This simplifies to:
A=14π∫2π0(1+cos(ϕ))dϕ
We can split the integral into two parts:
A=14π(∫2π01dϕ+∫2π0cos(ϕ)dϕ)
1. The first integral:
∫2π01dϕ=2π
2. The second integral:
∫2π0cos(ϕ)dϕ=0
(since the integral of cosine over one complete cycle is zero).
Now substituting these values back:
A=14π(2π+0)=2π4π=12
Thus, the average value of cos2(ϕ2) over one cycle is:
12
Topper's Solved these Questions
Similar Questions
Knowledge Check
The voltage over a cycle varies as
V=V0sinωt for 0≤t≤πω
=−V0sinωt for πω≤t≤2πω
The average value of the voltage one cycle isAV0√2BV02CzeroD2V0πAssertion: Average value of AC over a complete cycle is always zero.
Reason: Average value of AC is always defined over half cycle.AIf both assertion ans reason are true ans reaason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion istrue but reason is false.DIf both assertion and reason are false.The first acceptor of CO2 in Calvin cycle is
APGABRuBPCPGALDRuP
The average value of a function f(x) over the interval [a,b] is the number μ=1b−a∫baf(x)dx. The square root {1b−a∫baf2(x)dx}12 is called the root mean square of f on [a,b]. The average value μ is attained if f is continuous on [a,b].
The average value of f(x)=cos2xsin2x+4cos2x on [0,π2] is
View SolutionThese question consists of two statements each linked as Assertion and Reason. While answering these question you are required to choose any one of the following five responses.
Assertion: Average value of current in half the cycle an AC circuit can't be zero.
Reason: For positive half cycle average value of current is 2π i0, where i0 is the peak value current. In time interval from t1 to t2 average value of current will be zero.
View SolutionWhat are the average values of the following in a normal adult human?
Arterial PCO2
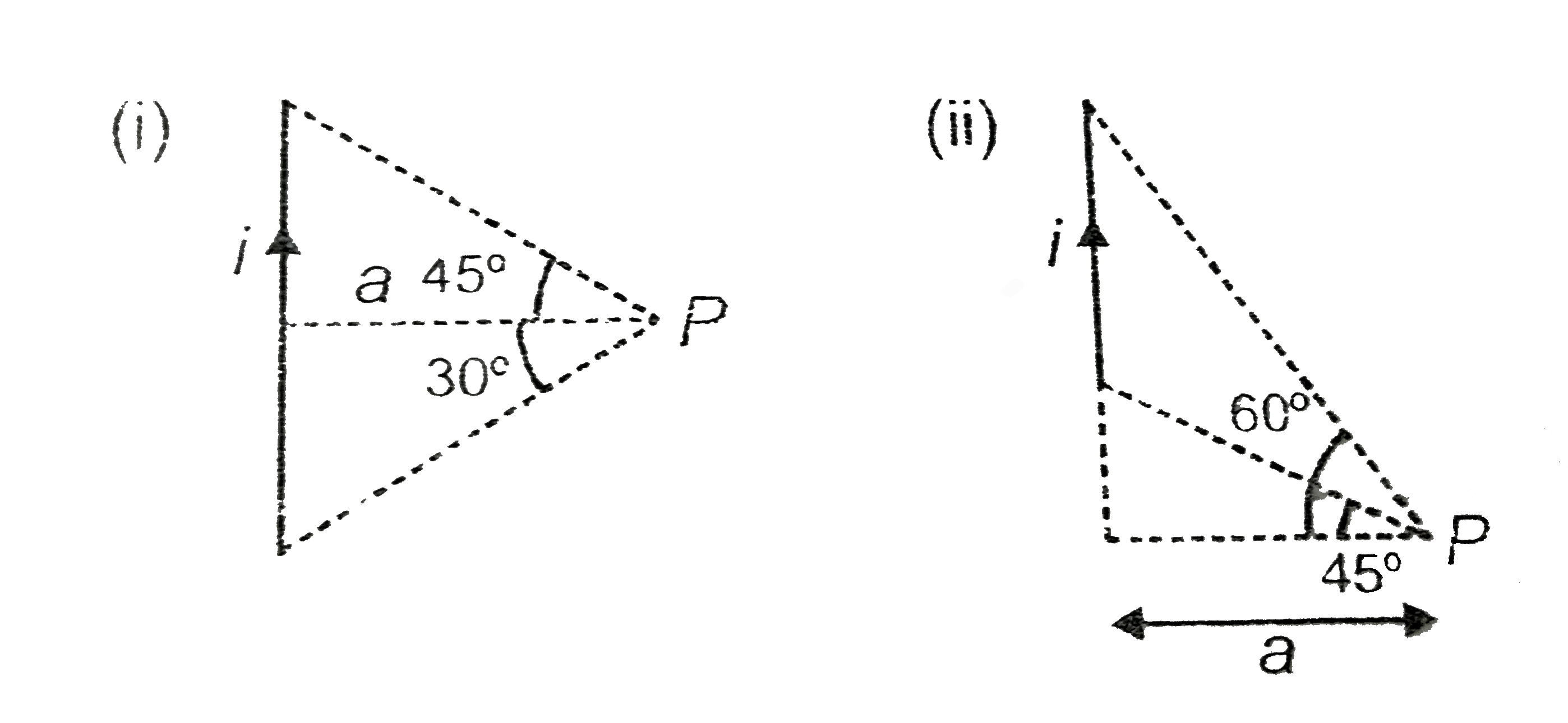
View SolutionWhat are value of ϕ1,ϕ2 and r to find out magnetic field at P in the following cases ?
View SolutionThe average velocity of CO2 at T K is 9×104cms−1. The value of T is
View Solution