Two waves of equal amplitude a from two coherent sources (S1&S2) interfere at a point R such that S2R−S1R=1.5λThe intensity at point R Would be
Zero
2a2
5a2
6a2
The correct Answer is:A
Step by step video & image solution for Two waves of equal amplitude a from two coherent sources (S_1 & S_2) interfere at a point R such that S_2R-S_1R =1.5 lambdaThe intensity at point R Would be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
When two waves of intensities l1andl2 coming from coherent sources interfere at a point P, where phase difference is ϕ, then resultant intensity (lres) at point P would be
View SolutionThe wavelength of sound waves arriving at P from two coherent sources S1 and S2 is 4 m as shown. While intensity of each wave is I0 the resultant intensity at point P is 2I0 find minimum value of x
_PHY_E06_238_Q01.png)
View Solution
Knowledge Check
In the case of light waves from two coherent sources S1 and S2, there will be constructive interference at an arbitrary point P, the path difference S1P−S2P is
A(n+12)λBnλC(n−12)λDλ2
In the figure , the intensity of waves arriving at D from two coherent soucrces s1ands2isI0. The wavelength of the wave is λ=4m . Resultant intensity at D will be

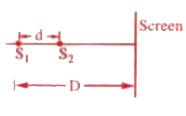
View SolutionTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be

View SolutionTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be

View SolutionTwo coherent sources S1 and S2 are separated by a small distance d. The fringes obtained on the screen will be:
View SolutionIn Young's double slit experiment, an interference pattern is obtained on a screen by a light of wavelength 6000Å, coming from the coherent sources S1 and S2. At certain point P on the screen third dark fringe is formed. Then the path difference S1P−S2P in microns is
View SolutionS1andS2 are two coherent sources of radiations separated by distance 100.25λ, where λ is the wave length of radiation. S1 leads S2 in phase by π/2.A and B are two points on the line joining S1andS2 as shown in figure.The ratio of amplitudes of component waves from source S1andS2 at A and B are in ratio 1:2. The ratio of intensity at A to that of B (IAIB) is

View SolutionS1andS2 are two coherent sources of radiations separated by distance 100.25λ, where λ is the wave length of radiation. S1 leads S2 in phase by π/2.A and B are two points on the line joining S1andS2 as shown in figure.The ratio of amplitudes of component waves from source S1andS2 at A and B are in ratio 1:2. The ratio of intensity at A to that of B (IAIB) is

View Solution
