One mole of an ideal gas undergoes change of state from (4 L, 3 atm) to (6 L, 5 atm). If the change in internal energy is 45 L-atm then the change of enthalpy for the process is
27 L-atm
45 L-atm
55 L-atm
63 L-atm
The correct Answer is:D
To find the change in enthalpy (ΔH) for the process, we can use the relationship between change in enthalpy, change in internal energy (ΔU), and the work done by the system. The formula we will use is:
ΔH=ΔU+Δ(PV)
Where:
- ΔH = change in enthalpy
- ΔU = change in internal energy
- Δ(PV) = change in pressure-volume product
Step 1: Identify the given values
- Change in internal energy (ΔU) = 45 L-atm
- Initial state: P1 = 3 atm, V1 = 4 L
- Final state: P2 = 5 atm, V2 = 6 L
Step 2: Calculate the initial and final PV values
- Initial PV (P1V1):
P1V1=3atm×4L=12L-atm
- Final PV (P2V2):
P2V2=5atm×6L=30L-atm
Step 3: Calculate the change in PV (Δ(PV))
Δ(PV)=P2V2−P1V1=30L-atm−12L-atm=18L-atm
Step 4: Substitute values into the enthalpy change equation
Now we can substitute the values into the enthalpy change formula:
ΔH=ΔU+Δ(PV)=45L-atm+18L-atm=63L-atm
Final Answer
The change in enthalpy (ΔH) for the process is:
ΔH=63L-atm
---
- ΔH = change in enthalpy
- ΔU = change in internal energy
- Δ(PV) = change in pressure-volume product
- Change in internal energy (ΔU) = 45 L-atm
- Initial state: P1 = 3 atm, V1 = 4 L
- Final state: P2 = 5 atm, V2 = 6 L
- Initial PV (P1V1):
P1V1=3atm×4L=12L-atm
P2V2=5atm×6L=30L-atm
Δ(PV)=P2V2−P1V1=30L-atm−12L-atm=18L-atm
Now we can substitute the values into the enthalpy change formula:
ΔH=ΔU+Δ(PV)=45L-atm+18L-atm=63L-atm
The change in enthalpy (ΔH) for the process is:
ΔH=63L-atm
Topper's Solved these Questions
Similar Questions
One mole of an ideal gas undergoes a change of state (2.0) atm, 3.0 L) to (2.0 atm, 7.0 L) with a change in internal energy (ΔU)=30 L-atm. The change in enthalpy (ΔH) of the process in L-atm :
View SolutionOne mole of non− ideal gas undergoes a change of state (1.0atm,3.0L,200K) to (4.0atm,5.0L,250K) with a change in internal energy (ΔU)=40L−atm. The change in enthalpy of the process in L−atm,
View SolutionOne mole of a non-ideal gas undergoes a change of state from (2,0 atm, 3.0 L, 100 K) to (4.0 atm, 5.0 L, 250 K) with a change in internal energy, ΔU=30.0 Latm. The change on enthalpy of process in (L - atm) is
View SolutionOne mole of a non-ideal gas undergoes a change of state (2.0atm,3.0L,95K)→(4.0atm,5.0L,245K)
With a change in internal energy ΔE=30L atm. The change in enthalpy (ΔH) in the process in L-atm is
View SolutionChange in internal energy in an isothermal process for ideal gas is
View SolutionOne mole of a non-ideal gas undergoes a change of state (2.0atm,3.0L,95K)→(4.0atm,5.0L,245K) with a change in internal energy , ΔU=30.0L.atm. Calculate change in enthalpy of the process in L.atm.
View SolutionOne mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure,
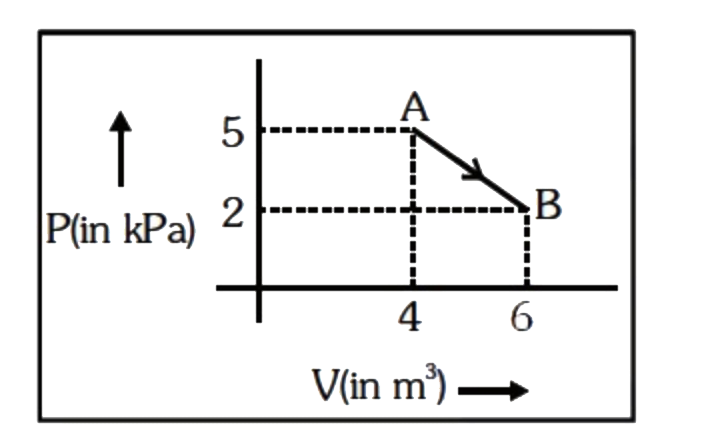
The change in internal energy of the gas during the transition is :
View SolutionOne mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure
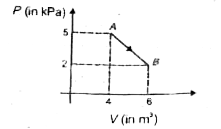
The change to internal energy of the gas during the transition is
View Solution0.5 moles of an ideal monoatomic gas undergoes a thermodynamic process from A to B as shown in figure. The change in internal energy of the gas during the process from A to B is
View SolutionOne mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in (figure). The change in internal energy of the gas during the transition is (γ=3/5)
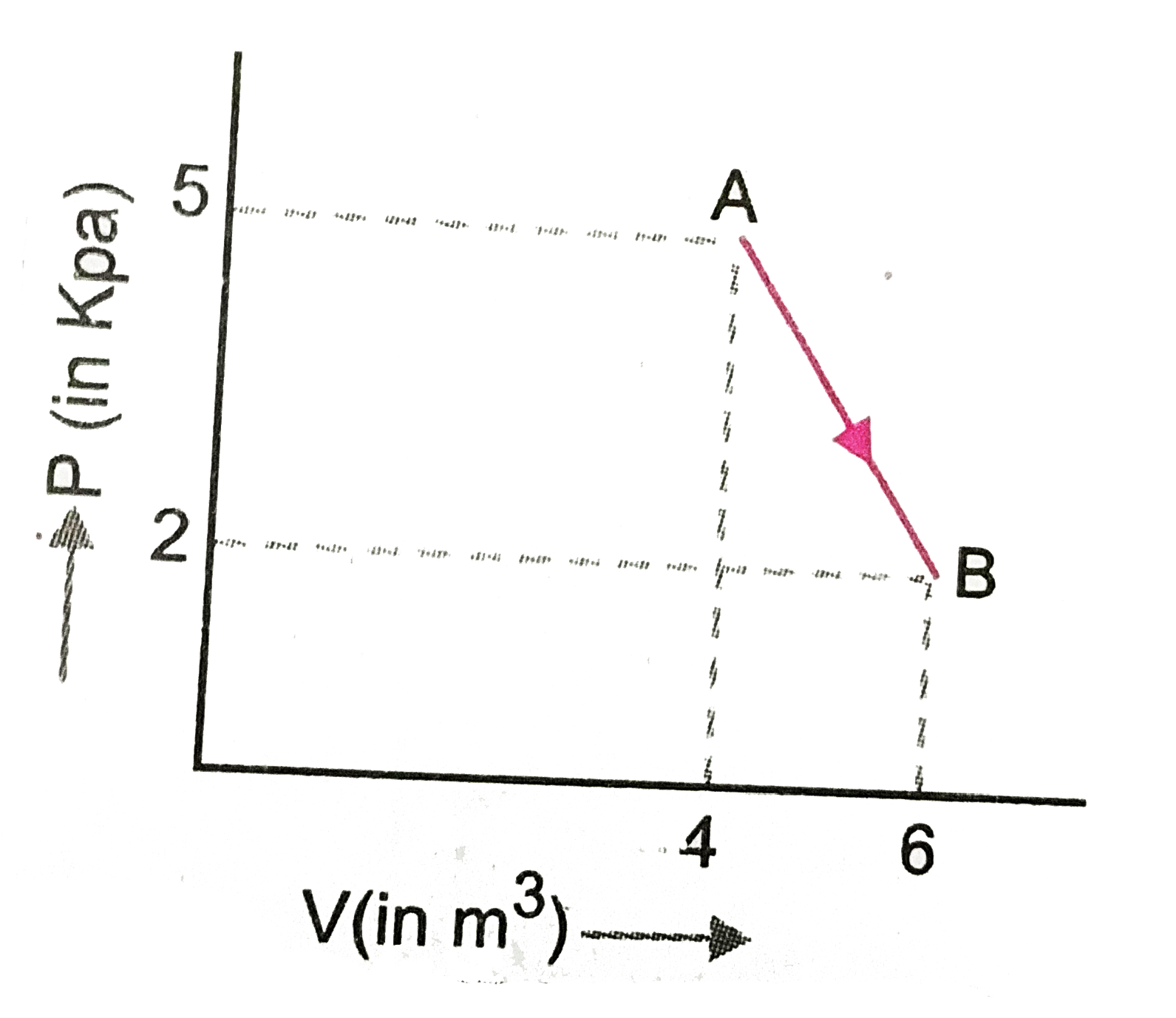
View Solution
