An inductor of inductance L = 8 H and a resistor of resistance R = 2Ω are connected in series with a battery of emf E = 10 V as shown in the figure. If the switch is closed at t = 0, then the voltage drop across the inductor at t = 1 s will be in volts)
52e−12
5e−14
58e−12
10e−14
To solve the problem, we need to find the voltage drop across the inductor at t=1 second after the switch is closed. We can use the relationship between the current through the inductor and the voltage drop across it.
1. Identify the given values:
- Inductance L=8H
- Resistance R=2Ω
- EMF E=10V
2. Write the formula for current in an RL circuit:
The current I(t) in an RL circuit after the switch is closed can be expressed as:
I(t)=ER(1−e−RLt)
3. Substitute the values into the equation:
I(t)=102(1−e−28t)=5(1−e−14t)
4. Calculate the current at t=1s:
I(1)=5(1−e−14⋅1)=5(1−e−14)
5. Find the derivative of current with respect to time:
The voltage drop across the inductor VL can be expressed as:
VL=LdIdt
To find dIdt, we differentiate I(t):
dIdt=ER⋅ddt(1−e−RLt)=ER⋅(0+RLe−RLt)
dIdt=ELe−RLt
6. Substitute the values into the derivative:
dIdt=108e−28t=54e−14t
7. Calculate dIdt at t=1s:
dIdt∣∣∣t=1=54e−14≈54⋅0.7788≈0.9748A/s
8. Calculate the voltage drop across the inductor:
VL=LdIdt=8⋅0.9748≈7.7984V
Final Answer:
The voltage drop across the inductor at t=1s is approximately 7.8V.
---
- Inductance L=8H
- Resistance R=2Ω
- EMF E=10V
The current I(t) in an RL circuit after the switch is closed can be expressed as:
I(t)=ER(1−e−RLt)
I(t)=102(1−e−28t)=5(1−e−14t)
I(1)=5(1−e−14⋅1)=5(1−e−14)
The voltage drop across the inductor VL can be expressed as:
VL=LdIdt
To find dIdt, we differentiate I(t):
dIdt=ER⋅ddt(1−e−RLt)=ER⋅(0+RLe−RLt)
dIdt=ELe−RLt
dIdt=108e−28t=54e−14t
dIdt∣∣∣t=1=54e−14≈54⋅0.7788≈0.9748A/s
VL=LdIdt=8⋅0.9748≈7.7984V
The voltage drop across the inductor at t=1s is approximately 7.8V.
Similar Questions
An inductor L and a resistance R are connected in series with a battery of emf E and a switch. Initially the switch is open. The switch is closed at an instant t = 0. Select the correct alternatives
View SolutionAn inductor of reactance XL=4Ω and resistor of resistance R=3Ω are connected in series with a voltage source of emf ε=(20V)[sin(100π(rads))t]. The current in the circuit at any time t will be
View Solution
Knowledge Check
- Question 1 - Select One
A pure inductor L, a capactior C and a resistance R are connected across a battery of emf E and internal resistance r as shows in Fig. Switch SW is closed at t=0, select the correct altermative (S).
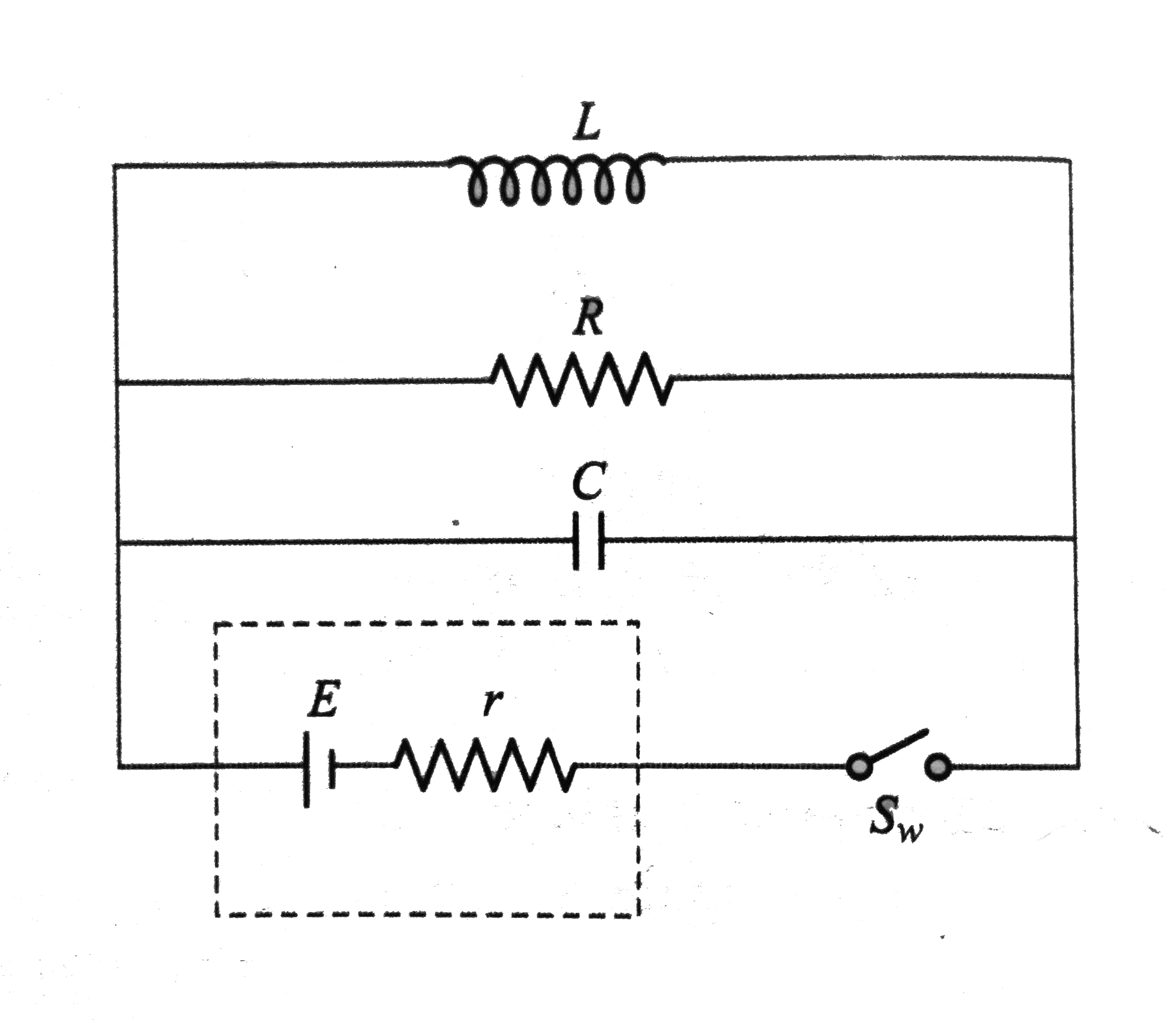 ACurrent through resistance R is zero all the time.BCurrent through resistance R is zero at t = 0 and t→∞.CMaximum charge stored in the capacitor is Cε.DMaximum energy stored in the inductor is equal to the maximum energy stored in the capacitor.
ACurrent through resistance R is zero all the time.BCurrent through resistance R is zero at t = 0 and t→∞.CMaximum charge stored in the capacitor is Cε.DMaximum energy stored in the inductor is equal to the maximum energy stored in the capacitor.
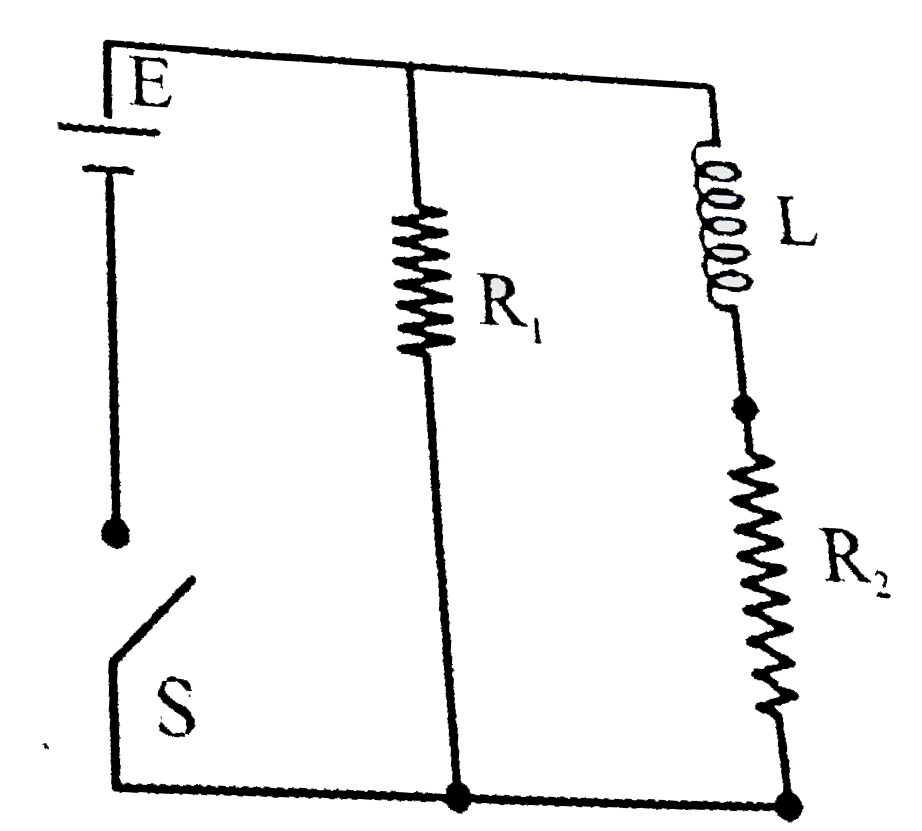
An inductor of inductance L = 400 mH and resistors of resistance R1=2Ω and R2=2Ω are connected to a battery of emf 12 V as shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at t=0. The potential drop across L as a function of time is
 View Solution
View SolutionAn inductor of inductance L = 400 mH and resistors of resistance R1=2Ω and R2=2Ω are connected to a battery of emf 12 V as shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at t=0. The potential drop across L as a function of time is
 View Solution
View SolutionAn inductor of inductance L = 400 mH and resistors of resistance R1=2Ω and R2=2Ω are connected to a battery of emf 12 V as shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at t=0. The potential drop across L as a function of time is
 View Solution
View SolutionAn inductor of inductance L=400mH and resistors of resistances R1=2Ω and R2=2Ω are connected to a battery of emf E=12V as shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at time t=0.

What is the potential dro across L s a function of time? After the steady state is reached, the switch is opened. What is the direction ad the magnitude of current throough R1 as a function of time?View SolutionAn inductor of 2 H and a resistance of 10Ω are connects in series with a battery of 5 V. The initial rate of change of current is
View Solution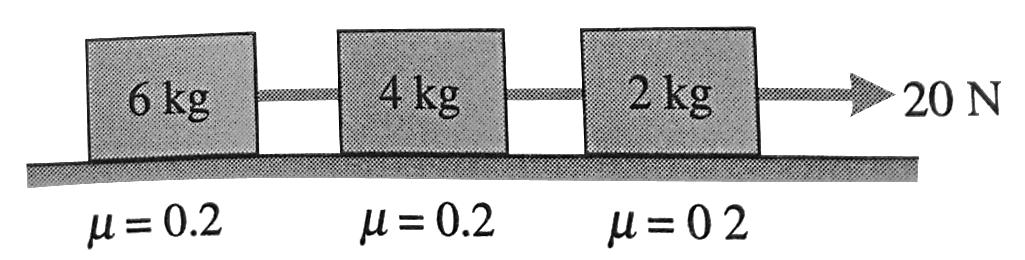
Three blocks of masses 6 kg, 4 kg and 2 kg are pulled on a rough surface by applying a constant force 20 N. The values of coefficient of friction between blocks and suface are shown in figure.
Q. Friction force on 6 kg block isView SolutionAn inductor L and a resistor R are connected in series to a battery, through a key/switch. Show graphically, how current decreases with time when the key/switch is opened.
View Solution

