force F is applied at the topmost point of block of mass M. The force required to topple the block before sliding is (µ = coefficient of friction) 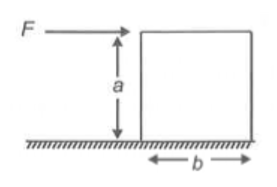
a.F>(Mgb2a)
b.F<µMg
c.F>(Mga2b)
d.Both (1) & (2)
Step by step video & image solution for force F is applied at the topmost point of block of mass M. The force required to topple the block before sliding is (µ = coefficient of friction) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
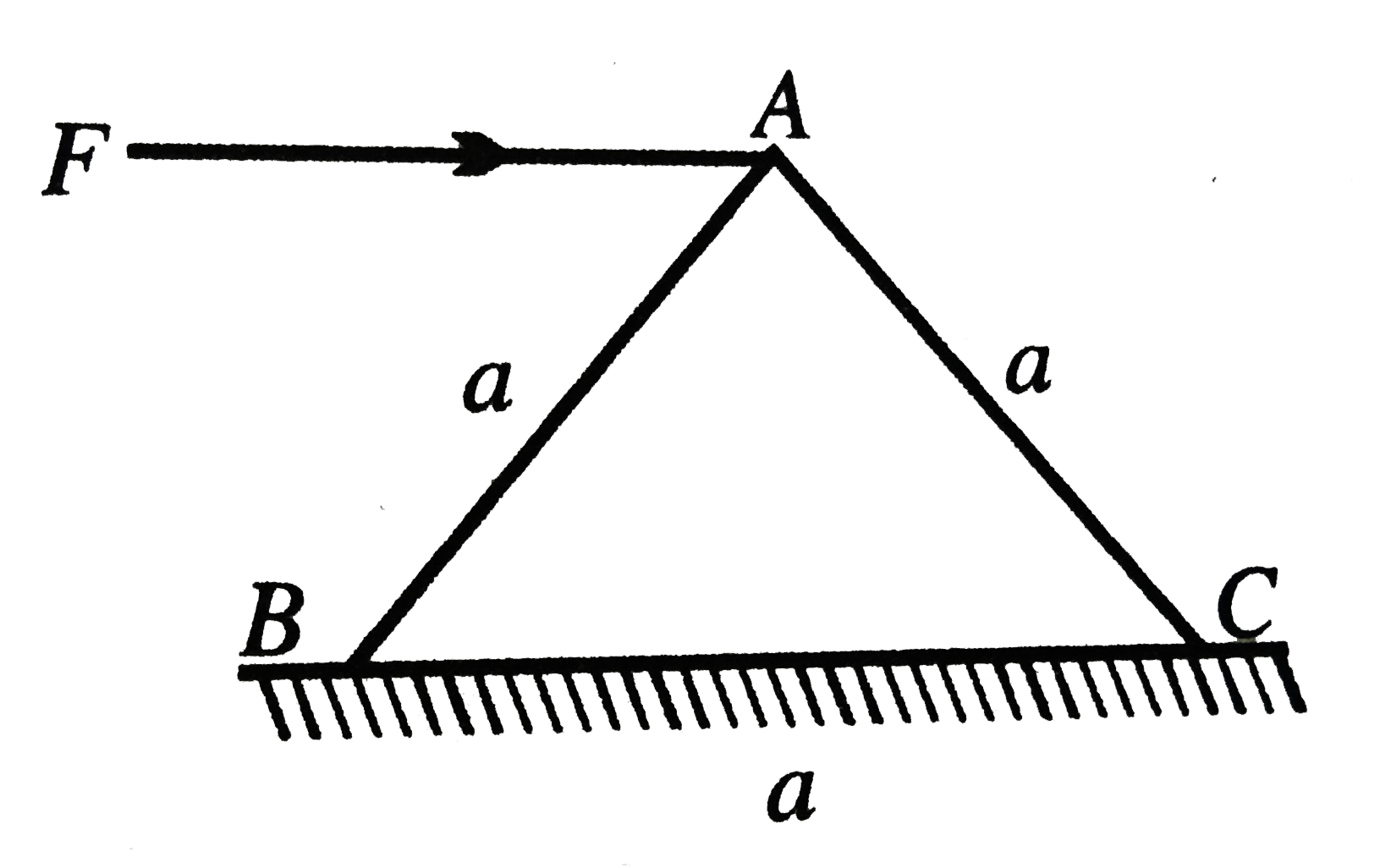
A horizontal force F is applied at the top of an equilateral triangular block having mass m. The minimum coefficient of friction required to topple the block before translation is μ,find 100μ?(√3=1.74)
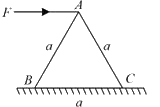
View SolutionA horizontal force F is applied at the top of an equilateral triangular block having mass m. The minimum coefficient of friction required to topple the block before translation will be
View SolutionA cubical box of side length L rests on a rough horizontal surface having coefficient of friction μ. A variable horizontal force F=αt is applied on the top of the block as shown in figure, where α is a constant and t is time. The coefficient of friction is sufficient so that the block does not slide before toppling. The graph between torque due to normal reaction about end B and time before toppling start is

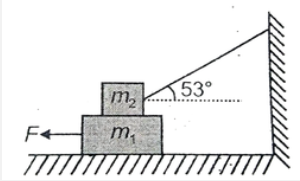
View SolutionCalculate the Force (F) required to cause the block of mass m1=20kg just to slide under the block of mass m2=10kg [ coefficient of friction μ=0⋅25 for all surfaces ]
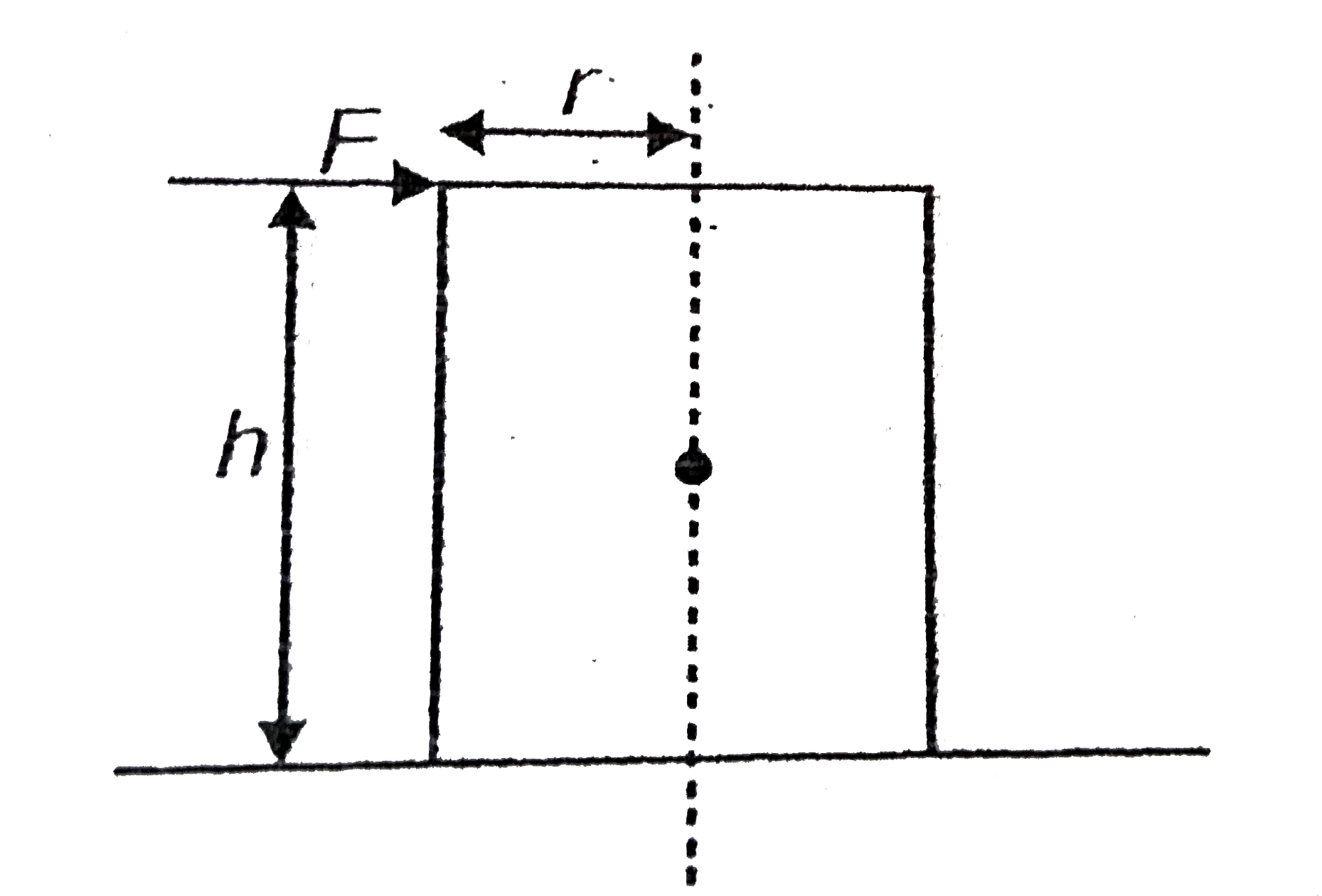
View SolutionA force -F is applied at the topmost point of a cylinder of radius r and height h.
(a) If the cylinder remains at rest, then find distance of line of action of normal reaction from center of mass.
(b) Find coefficient of friction required so that the cylinder tooples before sliding.
View SolutionA20 kg block is initally at rest. A 75 N force is required to set the block in motion. After the motion starts, a force of 60 N is required to keep the block moving with constant speed. The coefficient of static friction is
View SolutionA horizontal force F is applied to a homogeneous rectangular block of mass m, width b and height H. The block moves with constant velocity, the coefficient of friction is μk.
a. What is the greater height h at which the force F can be applied so that the block will slide without tipping over ?
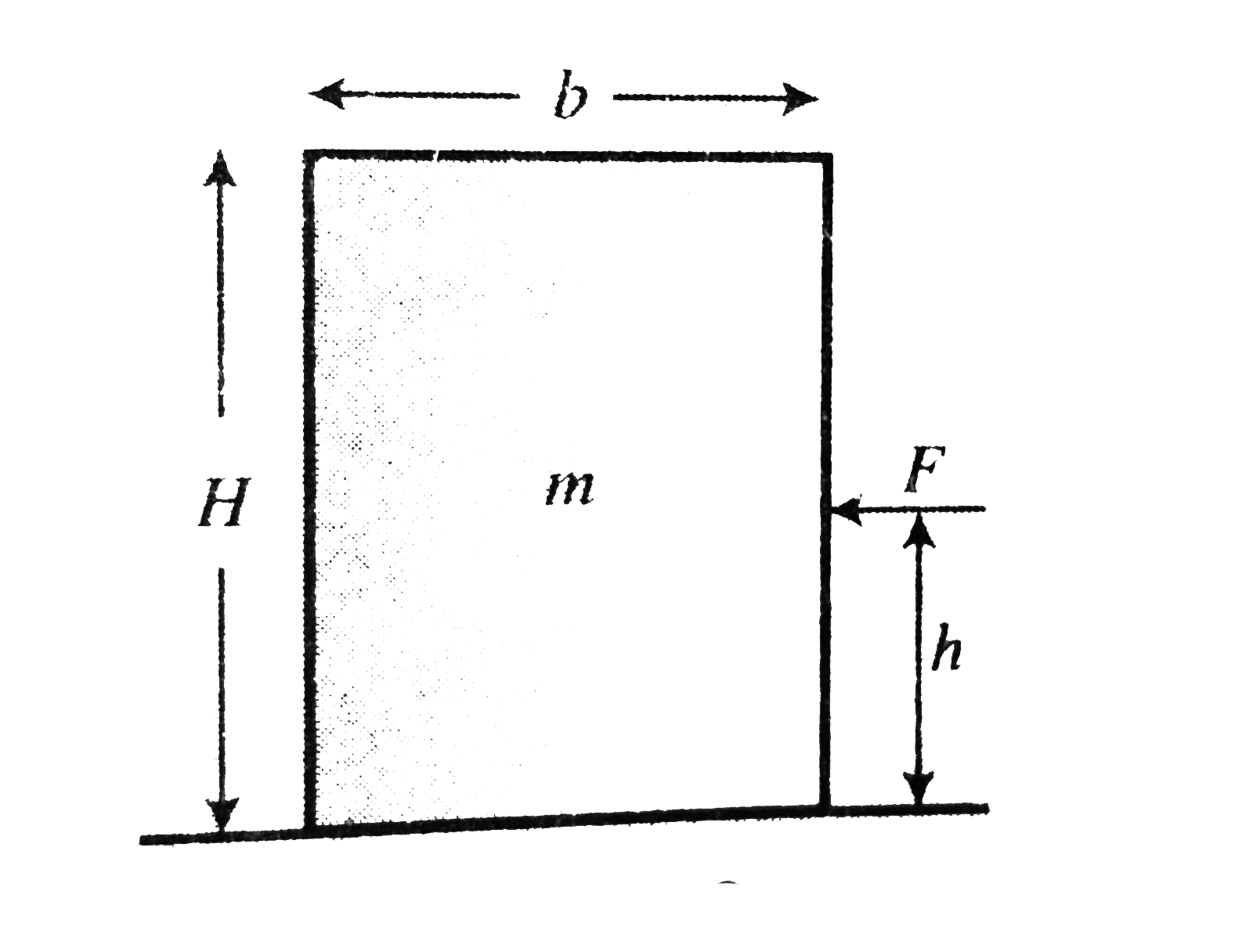
b. Through which point on the bottom face of the block will the resultant of the friction and normal forces act if h=H/2?
c. If the block is at rest and coefficient of static friction is μs what are the various criteria for which sliding or tipping occurs?
View SolutionA varying horizontal force F= at act on a block of mass m kept on a smooth horizontal surface An identical block is kept on the first block. The coefficient of friction between the blocks is μ . The time after which the relative sliding between the blocks prevails is
View SolutionA force of 200N is applied as shown in the figure on block of 3 kg. The coefficient of friction between the block and the wall is 0.3. Find the friction acting on the block. (in N) {Take g = 10 m/s2

View SolutionA cubical block of edge length 1 m and density 800 kg m−3 rests on a rough horizontal surface with coefficient of friction μ. A horizontal force F is applied on the block as shown in figure. If the coefficient of friction is sufficiently large so that the block does not slide bofore toppling, then the minimum value of F to topple the block is [Take g = 10 ms−2]

View Solution
