A prism of mass M is placed on a horizontal surface. A block of mass m slides on the prism, which in tum slides on the horizontal surface. Assuming all surfaces to be frictionless, find the acceleration of block with respect to prism.

Text Solution

Verified by Experts

Let $a_{0}$ be the acceleration of prism in the backward direction. The mass .m. is placed on non-inertial frame, therefore it is acted on by fictitious force $m a_{0}$ in the forward direction. The forces acting on mass m are
i) Weight mg acting downward,

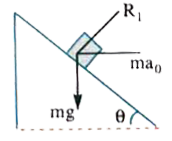
ii) Normal reaction R,
iii) Fictitious force $m a_{0}$
According free body diagram of .m. is shown in figure. Suppose block m slides down the prism with acceleration a. The equation of motion of .m. parallel to incline is
$m a_{0} cos θ + m g sin θ = m a$
$\Rightarrow a = a_{0} cos θ + g sin θ$ ........... (1)
The block is in equilibrium perpendicular to incline, so resolving force perpendicular to incline

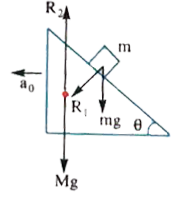
$R_{1} + m a_{0} sin θ = m g cos θ$ ........ (2)
Now we consider the forces acting on the prism. As prism is on ground (inertial frame) no fictitious force acts on it. The forces on prism are
i) Weight (Mg) downward.
ii) Normal force $R_{1}$ exerted by block
iii) Normal reaction $R_{1}$ exerted by ground
For horizontal motion of prism
$R_{1} sin θ = M a_{0} \Rightarrow R_{1} = \frac{M a_{0}}{sin θ}$ ......... (3)
substituting this value in (2) ,
$\frac{M a_{0}}{sin θ} + m a_{0} sin θ = m g cos θ$
This gives $a_{0} = \frac{m g sin θ cos θ}{M + m {sin}^{2} θ}$ ............ (4)
$∴$ From (1) , $a = \frac{m g sin θ {cos}^{2} θ}{M + m {sin}^{2} θ} + g sin θ$
$= \frac{(M + m) g sin θ}{M + m {sin}^{2} θ}$

|

Updated on:21/07/2023

Class 12 PHYSICS LAWS OF MOTION

Topper's Solved these Questions

Similar Questions

AAKASH SERIES-LAWS OF MOTION-PRACTICE EXERCISE

Home
Ask Doubt
Profile