A cubical block of mass M and side a is placed on a rough horizontal plane as shown in the figure A force F is acting on the block at height3a4 from the bottom. The minimum value of coefficient of friction (μ) such that block lopples without sliding will be
13
54
34
23
The correct Answer is:D
To solve the problem of finding the minimum value of the coefficient of friction (μ) such that the cubical block topples without sliding, we can follow these steps:
Step 1: Understand the Forces Acting on the Block
The block of mass M has a side length a. A force F is applied at a height of 3a4 from the base of the block. The weight of the block acts downward at its center of mass, which is located at a height of a2.
Step 2: Identify the Point of Rotation
To analyze the toppling condition, we consider the point of rotation to be at the edge of the block that is in contact with the ground. This edge is at a horizontal distance of a2 from the center of mass.
Step 3: Calculate the Torque due to the Applied Force
The torque τF due to the applied force F about the pivot point (the edge of the block) is given by:
τF=F⋅(3a4−a2)=F⋅(3a4−2a4)=F⋅a4
Step 4: Calculate the Torque due to the Weight of the Block
The torque τmg due to the weight of the block mg about the pivot point is:
τmg=mg⋅a2
Step 5: Set Up the Condition for Toppling
For the block to just begin to topple, the torque due to the applied force must equal the torque due to the weight of the block:
F⋅a4=mg⋅a2
Step 6: Simplify the Equation
Cancelling a from both sides gives:
F⋅14=mg⋅12
This simplifies to:
F=2mg
Step 7: Relate the Applied Force to Friction
The force F can also be expressed in terms of the coefficient of friction μ:
F=μmg
Step 8: Equate the Two Expressions for Force
From the two expressions for F:
μmg=2mg
Step 9: Solve for the Coefficient of Friction
Cancelling mg from both sides (assuming mg≠0):
μ=2
Step 10: Conclusion
Thus, the minimum value of the coefficient of friction μ such that the block topples without sliding is:
μ=23
The block of mass M has a side length a. A force F is applied at a height of 3a4 from the base of the block. The weight of the block acts downward at its center of mass, which is located at a height of a2.
To analyze the toppling condition, we consider the point of rotation to be at the edge of the block that is in contact with the ground. This edge is at a horizontal distance of a2 from the center of mass.
The torque τF due to the applied force F about the pivot point (the edge of the block) is given by:
τF=F⋅(3a4−a2)=F⋅(3a4−2a4)=F⋅a4
The torque τmg due to the weight of the block mg about the pivot point is:
τmg=mg⋅a2
For the block to just begin to topple, the torque due to the applied force must equal the torque due to the weight of the block:
F⋅a4=mg⋅a2
Cancelling a from both sides gives:
F⋅14=mg⋅12
This simplifies to:
F=2mg
The force F can also be expressed in terms of the coefficient of friction μ:
F=μmg
From the two expressions for F:
μmg=2mg
Cancelling mg from both sides (assuming mg≠0):
μ=2
Thus, the minimum value of the coefficient of friction μ such that the block topples without sliding is:
μ=23
Similar Questions
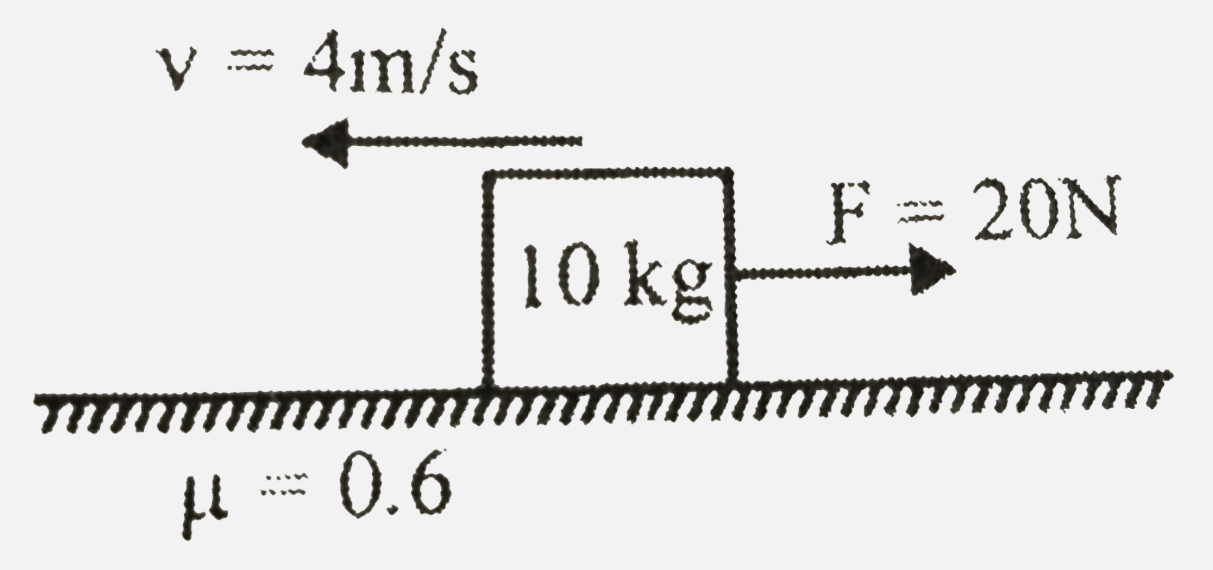
A block of mass 10 kg is moving on a rough surface as shown in figure. The frictional force acting on block is :-
View SolutionA block of mass m lying on a rough horizontal plane is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The minimum value of coefficient of friction of friction between the block and the surface for which the block will remain in equilibrium is

View Solution
Knowledge Check
A cubical box of side L rests on a rough horizontal surface with coefficient of friction p. A horizontal force F is a applied on the block as shown in Fig. 15.4.6. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is
 AinfinitesimalBmg/4Cmg/2Dmg (−1μ)
AinfinitesimalBmg/4Cmg/2Dmg (−1μ)
A block of mass m lying on a rough horizontal plane is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The minimum value of coefficient of friction of friction between the block and the surface for which the block will remain in equilibrium is

View SolutionA block of mass m lying on a rough horizontal plane is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The minimum value of coefficient of friction of friction between the block and the surface for which the block will remain in equilibrium is

View SolutionA block of mass 10 kg is kept on a rough inclined plane as shown in the figure. A force of 3 N is applied on the block. The coefficient of static friction between the plane and the block is 0.6 What should be the minimum value of force P, such that the block doesnot move downward? (take g=10ms−2)

View SolutionA block of mass 10 kg is kept on a rough inclined plane as shown in the figure. A force of 3 N is applied on the block. The coefficient of static friction between the plane and the block is 0.6 What should be the minimum value of force P, such that the block doesnot move downward? (take g=10ms−2)

View SolutionA block of mass m is pulled by a constant powert P placed on a rough horizontal plane. The friction coefficient the block and surface is μ. The maximum velocity of the block is.
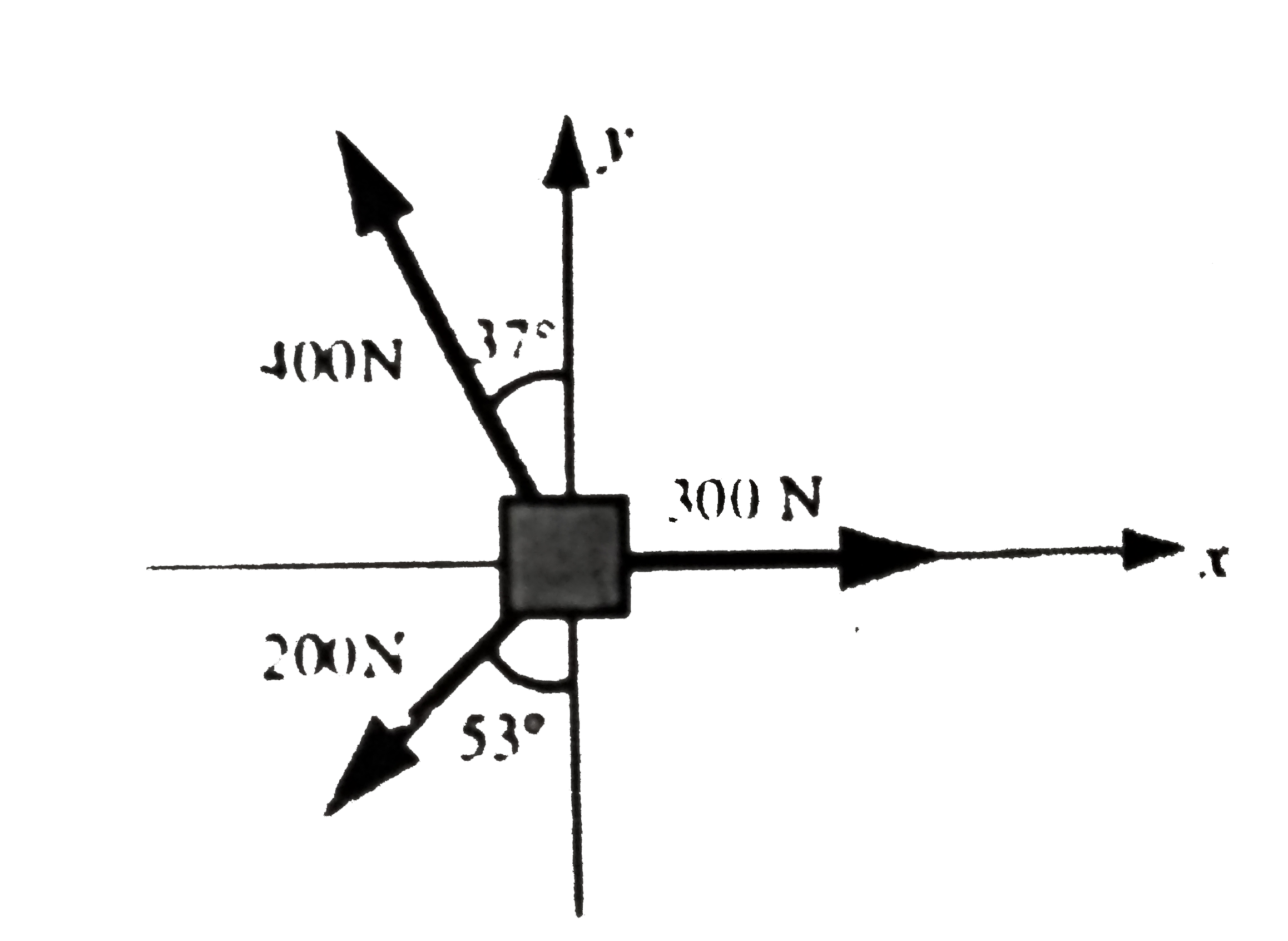
View SolutionA block is placed on a rough horizontal plane. Three horizontalforces are applied on the block as shown in the figure. If the block is in equilibrium, find the friction force acting on the block.
View SolutionA block of mass m is pulled by a force of constant power P placed on a rough horizontal plane. The friction coefficient between the block and the surface is μ. Then
View Solution
