A block of mass m is pulled by a force of constant power P placed on a rough horizontal plane. The friction coefficient between the block and the surface is μ. Then
The maximum velocity of the block during the motion is Pμmg
The maximum velocity of the block during the motion is P2μmg
The block's speed is never decreasing and finally becomes constant
The speed of the block first increases to a maximum value and then decreases
The correct Answer is:A, C
To solve the problem of finding the maximum velocity of a block of mass m being pulled by a force of constant power P on a rough horizontal plane with a coefficient of friction μ, we can follow these steps:
1. Understanding Power:
The power P exerted on the block can be expressed in terms of the force F acting on it and its velocity v:
P=F⋅v
2. Expressing Force in Terms of Power and Velocity:
Rearranging the formula for power, we can express the force as:
F=Pv
This equation shows that the force F is inversely proportional to the velocity v.
3. Frictional Force:
The frictional force Ff opposing the motion of the block is given by:
Ff=μ⋅m⋅g
where μ is the coefficient of friction, m is the mass of the block, and g is the acceleration due to gravity.
4. Condition for Maximum Velocity:
At maximum velocity Vmax, the net force acting on the block is zero. This means that the pulling force F equals the frictional force Ff:
F=Ff
Therefore, we can write:
PVmax=μ⋅m⋅g
5. Solving for Maximum Velocity:
Rearranging the equation to solve for Vmax:
Vmax=Pμ⋅m⋅g
Final Expression:
Thus, the maximum velocity Vmax of the block is given by:
Vmax=Pμ⋅m⋅g
---
The power P exerted on the block can be expressed in terms of the force F acting on it and its velocity v:
P=F⋅v
Rearranging the formula for power, we can express the force as:
F=Pv
This equation shows that the force F is inversely proportional to the velocity v.
The frictional force Ff opposing the motion of the block is given by:
Ff=μ⋅m⋅g
where μ is the coefficient of friction, m is the mass of the block, and g is the acceleration due to gravity.
At maximum velocity Vmax, the net force acting on the block is zero. This means that the pulling force F equals the frictional force Ff:
F=Ff
Therefore, we can write:
PVmax=μ⋅m⋅g
Rearranging the equation to solve for Vmax:
Vmax=Pμ⋅m⋅g
Thus, the maximum velocity Vmax of the block is given by:
Vmax=Pμ⋅m⋅g
Topper's Solved these Questions
- WORK, POWER AND ENERGYBook:DC PANDEY ENGLISHChapter:WORK, POWER AND ENERGYExercise:C Comprehension Type Questions
Explore 18 Videos
- WORK, POWER AND ENERGYBook:DC PANDEY ENGLISHChapter:WORK, POWER AND ENERGYExercise:D Matrix Matching Type Questions
Explore 10 Videos
- WORK, POWER AND ENERGYBook:DC PANDEY ENGLISHChapter:WORK, POWER AND ENERGYExercise:A Only One Option is Correct
Explore 42 Videos
- WORK, ENERGY AND POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY AND POWERExercise:MEDICAL ENTRACES GALLERY
Explore 33 Videos
Similar Questions
A block of mass m is pulled by a constant powert P placed on a rough horizontal plane. The friction coefficient the block and surface is μ. The maximum velocity of the block is.
View SolutionA block of mass M is pulled along a horizontal surface by applying a force at angle θ with the horizontal. The friction coefficient between the block and the surface is μ. If the block travels at a uniform velocity, find the work done by this applied force during a displacement d of the block.
View SolutionA block of mass M is pulled along a horizontal surface by applying a force at angle θ with the horizontal. The friction coefficient between the block and the surfasce is μ. If the block travels at a uniform velocity, find the work donen by this applied force during a displacement d of the blcok.
View SolutionA block of mass m is moving with a constant acceleration a on a rough horizontal plane. If the coefficient of friction between the block and ground is μ, the power delivered by the external agent in a time interval t from the beginning is equal to:
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
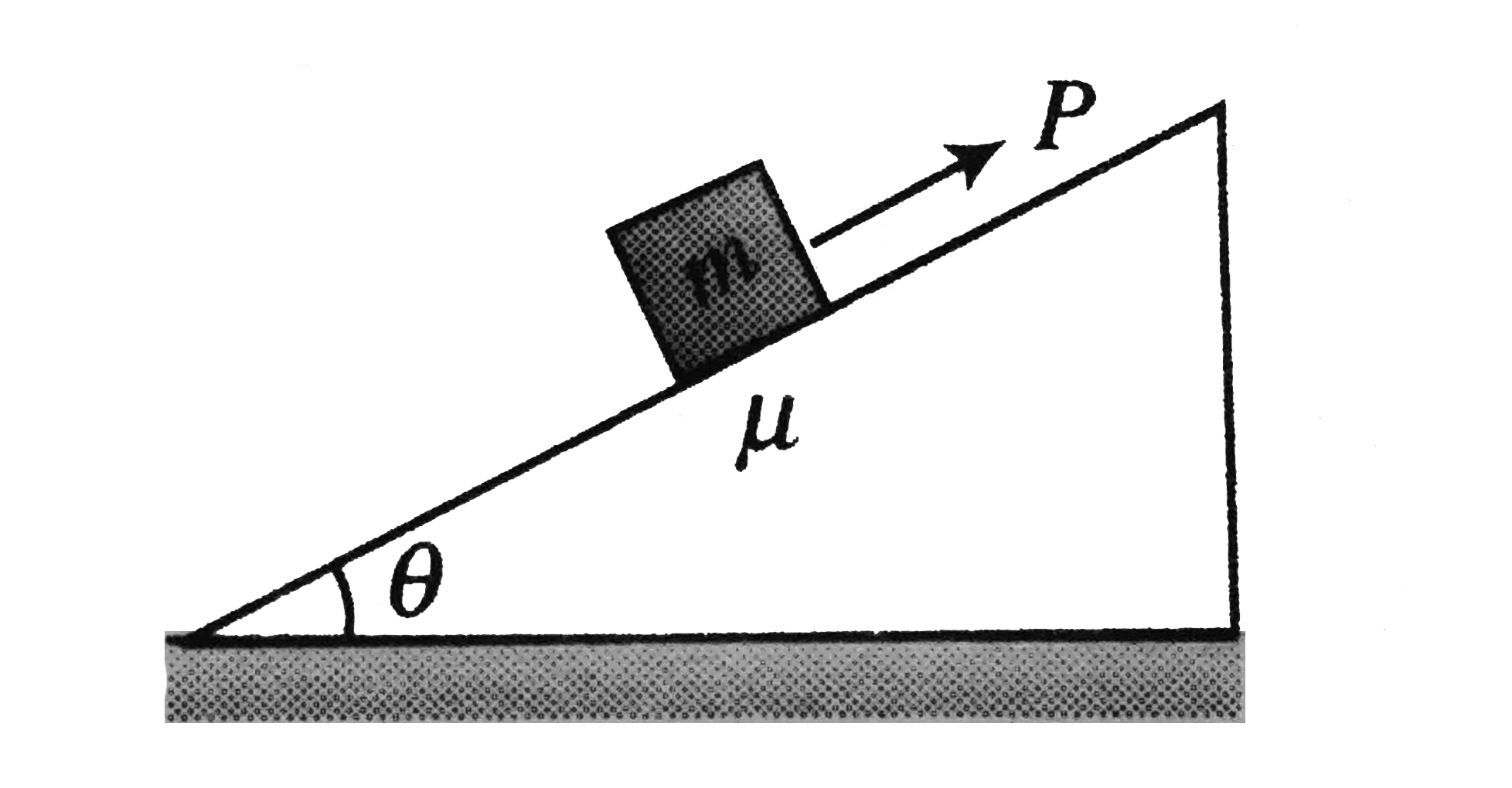
View SolutionA block of mass m is being pulled up a rough incline by an agent delivering constant power P. The coefficient of friction between the block and the incline is μ. The maximum speed of the block during the course of ascent is
View SolutionTwo block of masses m1 and m2 connected by a light spring rest on a horizontal plane. The coefficient of friction between the block and the surface is equal to μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1 in order to shift the other block?
View SolutionTwo block of masses m1 and m2 connected by a light spring rest on a horixontal plane. The cofficient of friction between the block and the surface is equal to μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1 in order to shift the other block?
View SolutionA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
View SolutionA block of mass M is kept on as rough horizontal surface. The coefficient of static frictionbetween the block and the surface is μ. The block is to be pulled by applying a force to it. What minimum force is needed to slide the block? In which direction should this force act?
View Solution
