A solid sphere of mass M and radius R is in pure rolling as shown in figure. The angular momentum of the sphere about the origin is (linear velocity of centre of mass is v0, in positive x-direction)
3MRV05(−K)
3MRV05(+K)
7MRV05(−K)
7MRV05(+K)
The correct Answer is:C
To find the angular momentum of a solid sphere of mass M and radius R that is rolling without slipping, we can follow these steps:
1. Identify the Parameters:
- Mass of the sphere: M
- Radius of the sphere: R
- Linear velocity of the center of mass: v0 (in the positive x-direction)
- Angular velocity ω can be related to the linear velocity as v0=Rω.
2. Calculate the Moment of Inertia:
The moment of inertia I of a solid sphere about its center is given by:
I=25MR2
3. Determine Angular Momentum about the Center of Mass:
The angular momentum LCM of the sphere about its center of mass is given by:
LCM=Iω
Substituting the expression for I:
LCM=25MR2⋅ω
Since ω=v0R:
LCM=25MR2⋅v0R=25MRv0
4. Calculate the Angular Momentum due to the Translation of the Center of Mass:
The angular momentum due to the translational motion of the center of mass about the origin is given by:
Ltrans=M⋅R⋅v0
Here, R is the distance from the origin to the center of mass.
5. Combine Both Contributions:
The total angular momentum L about the origin is the sum of the angular momentum about the center of mass and the angular momentum due to the translation:
L=LCM+Ltrans
Substituting the values we calculated:
L=25MRv0+MRv0
L=(25MRv0+55MRv0)=75MRv0
6. Direction of Angular Momentum:
Since the sphere is rolling in the positive x-direction, the angular momentum vector will point in the negative z-direction (using the right-hand rule). Thus, we can express it as:
L=75MRv0^k (in the negative z-direction)
or
L=−75MRv0^k
Final Answer:
The angular momentum of the sphere about the origin is:
L=−75MRv0^k
- Mass of the sphere: M
- Radius of the sphere: R
- Linear velocity of the center of mass: v0 (in the positive x-direction)
- Angular velocity ω can be related to the linear velocity as v0=Rω.
The moment of inertia I of a solid sphere about its center is given by:
I=25MR2
The angular momentum LCM of the sphere about its center of mass is given by:
LCM=Iω
Substituting the expression for I:
LCM=25MR2⋅ω
Since ω=v0R:
LCM=25MR2⋅v0R=25MRv0
The angular momentum due to the translational motion of the center of mass about the origin is given by:
Ltrans=M⋅R⋅v0
Here, R is the distance from the origin to the center of mass.
The total angular momentum L about the origin is the sum of the angular momentum about the center of mass and the angular momentum due to the translation:
L=LCM+Ltrans
Substituting the values we calculated:
L=25MRv0+MRv0
L=(25MRv0+55MRv0)=75MRv0
Since the sphere is rolling in the positive x-direction, the angular momentum vector will point in the negative z-direction (using the right-hand rule). Thus, we can express it as:
L=75MRv0^k (in the negative z-direction)
or
L=−75MRv0^k
The angular momentum of the sphere about the origin is:
L=−75MRv0^k
Similar Questions

A solid sphere of mass m and radius R is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.
View SolutionA disc of mass m and radius R moves in the x−y plane as shown in Fig. The angular momentum of the disc about the origin O at the instant shown is

View SolutionThree solid sphere of mass M and radius R are placed in contact as shown in figure. Find the potential energy of the system ?
View SolutionA solid sphere of mass M and radius R is pulled horizontally on a rough surface as shown in Fig. Choose the incorrect alternatives.

View SolutionA solid sphere of mass M and radius R is pulled by a force F as shown in figure . If the sphere does not slip over the surface , then frictional force acting on the sphere is

View SolutionA solid cylinder of mass M and radius R pure rolls on a rough surface as shown in the figure. Choose the correct alternative (s).

View SolutionA particle mass parallel to x-axis with constant velocity v as shown in the figure. The angular velocity of the particle about the origin O

View SolutionA cycle tyre of mass M and radius R is in pure rolling over a horizontal surface. If the velocity of the centre of mass of the tyre is v, then the velocity of point P on the tyre, shown in figure is
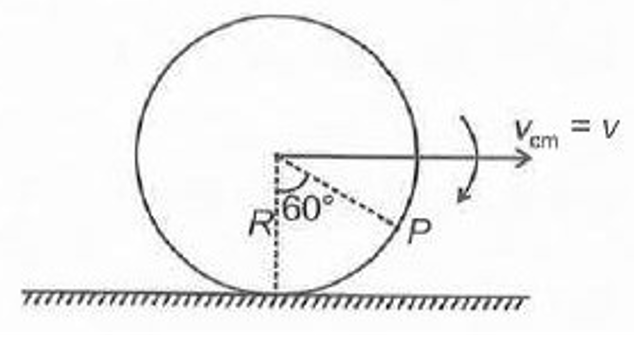
View SolutionA disc of mass M and Radius R is rolling with an angular speed ω on the horizontal plane. The magnitude of angular momentum of the disc about origin is:
View Solution
A solid sphere of mass M and radius R is hit by a cue at a height h above the centre C. for what value of h the sphere will rool without slipping ?
View Solution