A plank of mass 2m and length L is al rest on a frictionless horizontal floor At one end of it, a child of mass m is standing as shown in figure If child walks and reaches the other and then the distance travelled by child wrt ground will be
L3
L2
2L3
3L4
The correct Answer is:C
To solve the problem, we need to find the distance traveled by the child with respect to the ground when he walks from one end of the plank to the other. We will use the concept of the center of mass and the principle of conservation of momentum.
1. Identify the System:
- We have a plank of mass 2m and length L on a frictionless surface.
- A child of mass m is standing on one end of the plank.
2. Initial Center of Mass Calculation:
- The initial position of the center of mass (CM) of the system can be calculated using the formula:
xCM=m⋅0+2m⋅L2m+2m=0+mL3m=L3
- Here, the child is at position 0 and the plank’s center of mass is at L2.
3. Final Center of Mass Calculation:
- When the child walks to the other end of the plank, we need to find the new position of the center of mass. Let’s denote the distance the child walks as x.
- The final position of the child will be L (the other end of the plank).
- The new position of the center of mass will be:
x′CM=m⋅L+2m⋅L2m+2m=mL+mL3m=2L3
4. Conservation of Center of Mass:
- Since there are no external forces acting on the system, the center of mass of the system must remain constant. Therefore, the initial center of mass position must equal the final center of mass position:
L3=2L3−d
- Here, d is the distance the plank moves in the opposite direction due to the child walking.
5. Finding the Distance Traveled by the Child:
- The distance the child travels with respect to the ground can be calculated as:
Distancechild=L−d
- From the conservation of center of mass, we can find d:
d=L3
- Therefore, the distance traveled by the child with respect to the ground is:
Distancechild=L−L3=2L3
Final Answer:
The distance traveled by the child with respect to the ground is 2L3.
- We have a plank of mass 2m and length L on a frictionless surface.
- A child of mass m is standing on one end of the plank.
- The initial position of the center of mass (CM) of the system can be calculated using the formula:
xCM=m⋅0+2m⋅L2m+2m=0+mL3m=L3
- Here, the child is at position 0 and the plank’s center of mass is at L2.
- When the child walks to the other end of the plank, we need to find the new position of the center of mass. Let’s denote the distance the child walks as x.
- The final position of the child will be L (the other end of the plank).
- The new position of the center of mass will be:
x′CM=m⋅L+2m⋅L2m+2m=mL+mL3m=2L3
- Since there are no external forces acting on the system, the center of mass of the system must remain constant. Therefore, the initial center of mass position must equal the final center of mass position:
L3=2L3−d
- Here, d is the distance the plank moves in the opposite direction due to the child walking.
- The distance the child travels with respect to the ground can be calculated as:
Distancechild=L−d
- From the conservation of center of mass, we can find d:
d=L3
- Therefore, the distance traveled by the child with respect to the ground is:
Distancechild=L−L3=2L3
The distance traveled by the child with respect to the ground is 2L3.
Similar Questions
A plank of mas M and length L is at rest on as frictionless floor. The top surface of the plank has friction. At one end of it a man of mass m is standing as shown in figure. If the man walks towards the other end the find the distance, which the plank moves a till the man reaches the centre of the plank. b. till the man reaches the other end of the plank.

View SolutionA rod of mass m and length l is lying on a horizontal table. Work done in making it stand on one end will be
View SolutionA block of mass m and length l is kept at rest on a rough horizontal ground of friction coefficient μk. A man of mass m is standing at the right end. Now the man starts walking towards left and reaches the left end within time ‘t’. During this time, the displacement of the block is : (Assume the pressing force between the block and the ground remains constant and its value is same as it was initially. Also as sume that the block slides during the entire time (t))

View SolutionA uniform smooth rod (mass m and length l) placed on a smooth horizontal floor is it by a particle (mass m) moving on the floor, at a distance l4 from one end elastically (e=1). The distance travelled by the centre of the rod after the collision when it has completed three revolutions will be
View SolutionA uniform rope of mass (m) and length (L) placed on frictionless horizontal ground is being pulled by two forces FAandFB at its ends as shown in the figure. As a result, the rope accelerates toward the right.

Acceleration (A) of the rope is
View SolutionA flat car of mass M is at rest on a frictionless floor with a child of mass m standing at its edge. If the child jumps off from the car towards right with an initial velocity u, with respect to the car, find the velocity of the car after its jump.
View SolutionA strip of wood of mass M and length l is placed on a smooth horizontal surface. An insect of mass m starts at one end of the strip and walks to the other end in time t, moving with a constant speed. The speed of the insect as seen from the ground is
View SolutionA uniform rope of mass (m) and length (L) placed on frictionless horizontal ground is being pulled by two forces FAandFB at its ends as shown in the figure. As a result, the rope accelerates toward the right.

Expression Tx of tension at a point at distance x from the end A is
View SolutionA uniform rod of mass M and length L falls when it is made to stand on a smooth horizontal floor. The trajectories of the points P,Q and R as shown in the figure given below is best represented by :
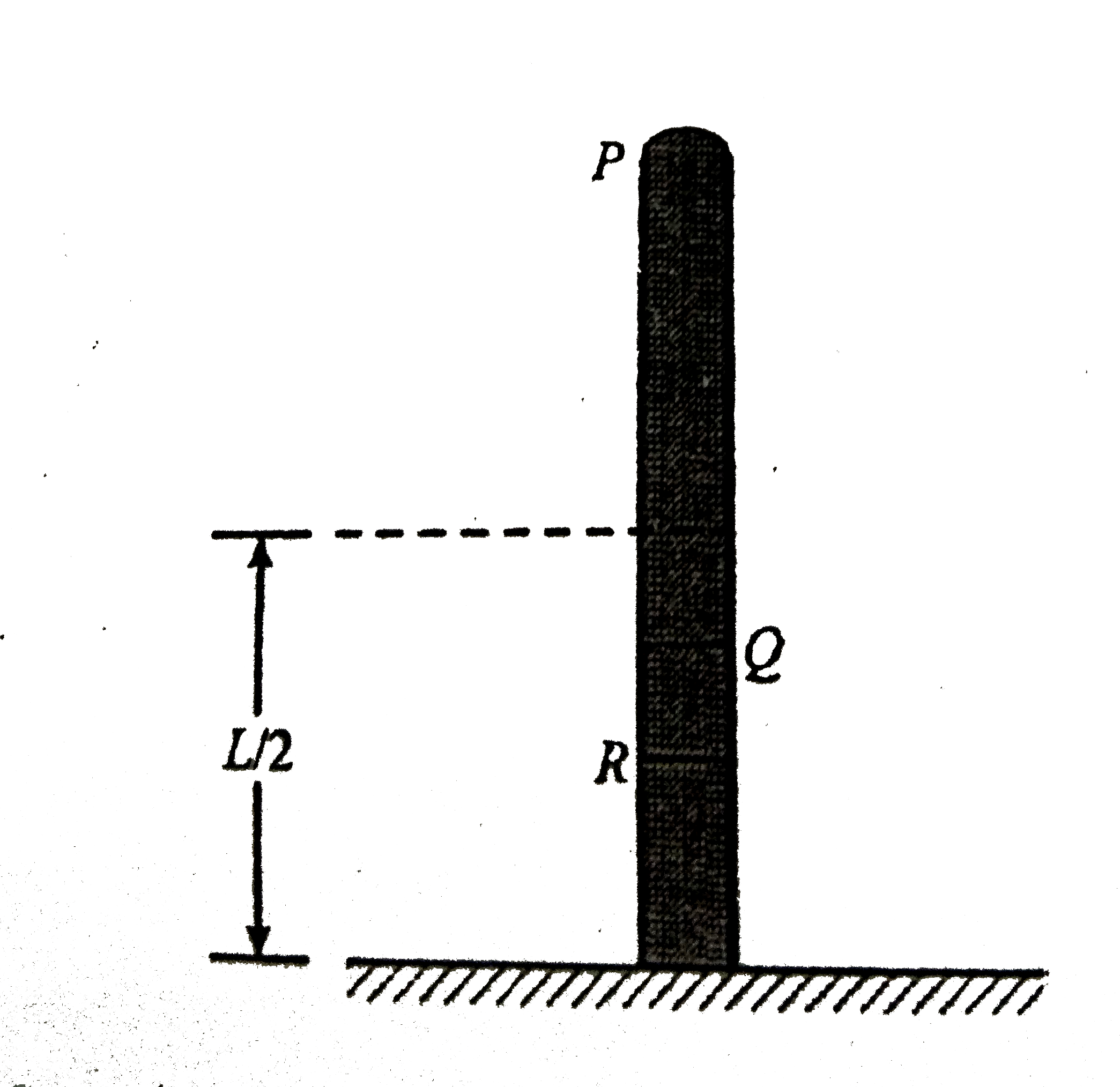
View SolutionA man of mass M stands at one end of a plank of length L Which lies at rest on a frictionless surface . The man walks to the other end of the plank. If the mass of the plank is 3M, the distance that the man moves relative to the ground is
View Solution
