A system of uniform rod of mass m and length 2R and a uniform disc of m and radius R are as shown in the figure. The moment of inertia of the system about the axis OO′ (perpendicular to plane of disc) will be
79mR212
41mR26
7mR26
25mR212
The correct Answer is:B
To find the moment of inertia of the system consisting of a uniform rod and a uniform disc about the axis OO' (perpendicular to the plane of the disc), we will calculate the moment of inertia of both components separately and then sum them up.
1. Identify the Components:
- We have a uniform rod of mass m and length 2R.
- We have a uniform disc of mass m and radius R.
2. Moment of Inertia of the Rod:
- The moment of inertia I of a rod about an axis perpendicular to its length and passing through one end is given by:
Irod=13mL2
- Here, L=2R, so substituting in:
Irod=13m(2R)2=13m(4R2)=43mR2
3. Moment of Inertia of the Disc:
- The moment of inertia I of a disc about an axis through its center and perpendicular to its plane is given by:
Idisc=12mR2
- However, since the axis OO' is not through the center of the disc but at a distance 2R from the center (the length of the rod), we need to use the parallel axis theorem:
I′=I+md2
- Here, d=2R, so:
I′disc=12mR2+m(2R)2=12mR2+4mR2=12mR2+8mR2=172mR2
4. Total Moment of Inertia:
- Now, we can find the total moment of inertia Inet of the system about the axis OO':
Inet=Irod+I′disc=43mR2+172mR2
- To add these fractions, we need a common denominator, which is 6:
Inet=86mR2+516mR2=596mR2
5. Final Result:
- Therefore, the moment of inertia of the system about the axis OO' is:
Inet=596mR2
- We have a uniform rod of mass m and length 2R.
- We have a uniform disc of mass m and radius R.
- The moment of inertia I of a rod about an axis perpendicular to its length and passing through one end is given by:
Irod=13mL2
- Here, L=2R, so substituting in:
Irod=13m(2R)2=13m(4R2)=43mR2
- The moment of inertia I of a disc about an axis through its center and perpendicular to its plane is given by:
Idisc=12mR2
- However, since the axis OO' is not through the center of the disc but at a distance 2R from the center (the length of the rod), we need to use the parallel axis theorem:
I′=I+md2
- Here, d=2R, so:
I′disc=12mR2+m(2R)2=12mR2+4mR2=12mR2+8mR2=172mR2
- Now, we can find the total moment of inertia Inet of the system about the axis OO':
Inet=Irod+I′disc=43mR2+172mR2
- To add these fractions, we need a common denominator, which is 6:
Inet=86mR2+516mR2=596mR2
- Therefore, the moment of inertia of the system about the axis OO' is:
Inet=596mR2
Similar Questions
Four rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY' will be

View SolutionThree rings each of mass M and radius R are arranged according to the figure. The moment of inertia of this system about an axis XX' on its plane would be

View Solution
Knowledge Check
From a uniform circular disc of radius R and mass 9M, a small disc of radius R3 is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is :
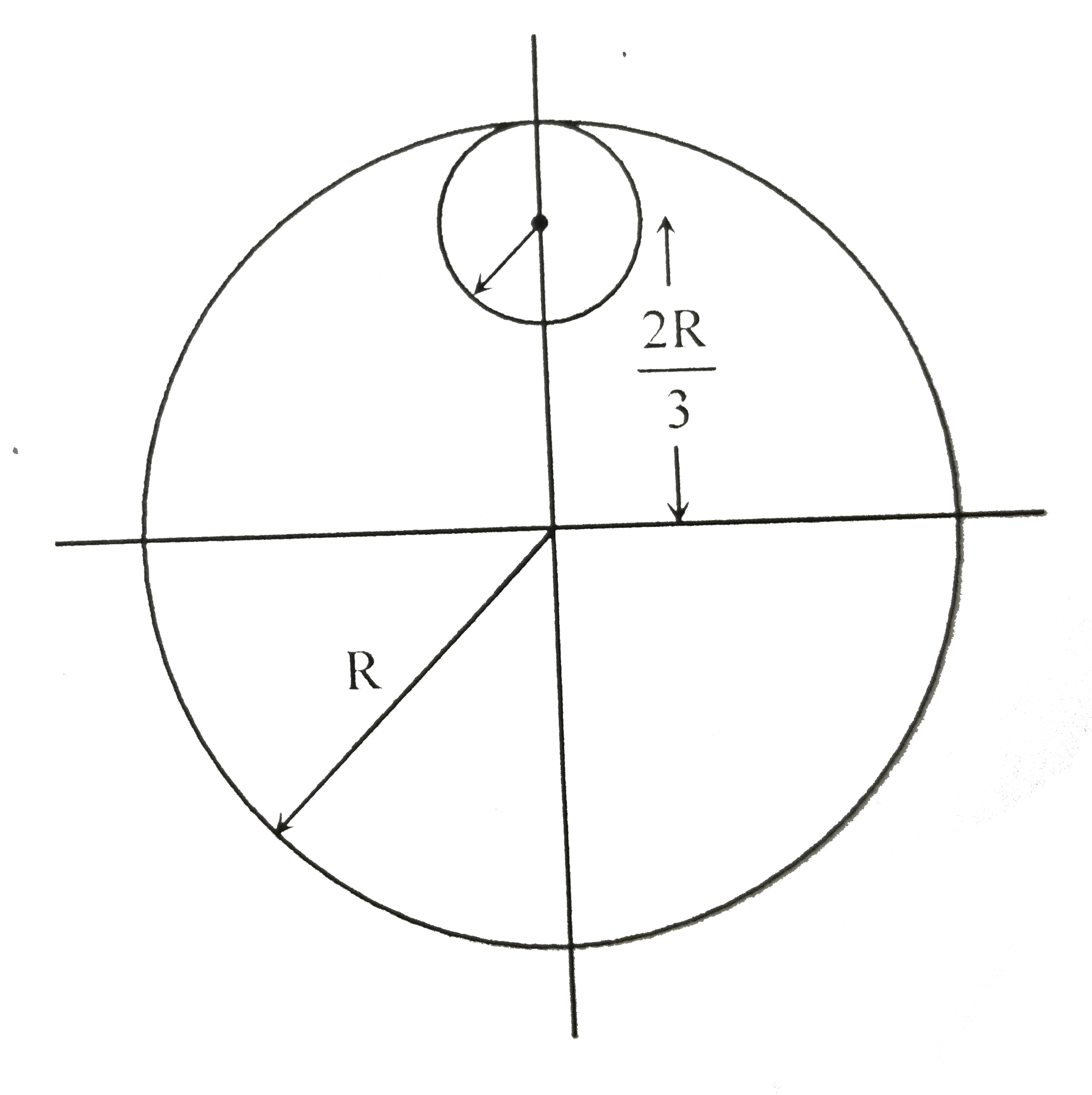 A4MR2B409MR2C40MR2D379MR2
A4MR2B409MR2C40MR2D379MR2
Two uniform rods each of mass M and length L are joined as shown in the figure. The moment of inertia of the system about line AB is kML2.Find the value of k.
View SolutionFour thin rods of same mass M and same length l, form a square as shown in figure. Moment of inertia of this system about an axis through centre O and perpendicular to its plane is

View SolutionFour identical uniform thin rods, each of mass m and length l are joined to a common point O as shown in the figure. Moment of inertia of the system about an axis passing through O and lying in the plane of rods is
View SolutionA uniform rod of mass m is bent into the form of a semicircle of radius R. The moment of inertia of the rod about an axis passing through A and perpendicular to the plane of the paper is

View SolutionA uniform rod of mass m is bent into the form of a semicircle of radius R. The moment of inertia of the rod about an axis passing through A and perpendicular to the plane of the paper is

View SolutionA disc of mass m and radius R has a concentric hole of radius r. Its moment of inertia about an axis through its center and perpendicular to its plane is
View SolutionA uniform rod of mass 2M is bent into four adjacent semicircles each of radius r, all lying in the same plane. The moment of inertia of the bent rod about an axis through one end A and perpendicular to plane of rod is

View Solution
