A small block of mass m is placed at the bottom of fixed circular smooth surface of radius R as shown in the figure If a velocity v. 14 gR is given to the block then maximum height from the bottom of circular surface, where block will leave the contact
5R3
3R2
R
R2
The correct Answer is:A
To solve the problem step by step, we will use the principles of conservation of energy and the conditions for circular motion.
1. Understanding the Problem:
A small block of mass m is placed at the bottom of a circular surface of radius R. It is given an initial velocity v0=√4gR. We need to find the maximum height h from the bottom of the circular surface where the block will leave contact with the surface.
2. Applying Conservation of Mechanical Energy:
The total mechanical energy at the bottom (initial state) is equal to the total mechanical energy at the height h (final state).
12mv20=mgh+12mv2
Here, v is the velocity of the block at height h.
3. Substituting the Initial Velocity:
Substitute v0=√4gR into the equation:
12m(4gR)=mgh+12mv2
Simplifying gives:
2mgR=mgh+12mv2
4. Rearranging the Equation:
Rearranging the equation to isolate v2:
12mv2=2mgR−mgh
v2=4gR−2gh
5. Condition for Leaving Contact:
For the block to leave the surface, the normal force N must be zero. The forces acting on the block in the vertical direction when it is at height h are:
mgcos(θ)=mv2R
Where θ is the angle from the vertical. Since N=0:
mgcos(θ)=mv2R
6. Substituting v2:
Substitute v2 from the previous step:
mgcos(θ)=m(4gR−2gh)R
Simplifying gives:
gcos(θ)=4gR−2ghR
7. Canceling g and Rearranging:
Cancel g (assuming g≠0):
cos(θ)=4R−2hR
Rearranging gives:
cos(θ)=4−2hR
8. Using the Cosine Relation:
From circular motion, we know:
h=R(1−cos(θ))
Substituting for cos(θ):
h=R(1−(4−2hR))
Simplifying gives:
h=R(−3+2hR)
h=−3R+2h
h−2h=−3R
−h=−3R⟹h=3R
9. Finding the Maximum Height:
The maximum height from the bottom of the circular surface where the block leaves contact is:
h=2R3
Final Answer:
The maximum height from the bottom of the circular surface where the block will leave contact is:
h=5R3
A small block of mass m is placed at the bottom of a circular surface of radius R. It is given an initial velocity v0=√4gR. We need to find the maximum height h from the bottom of the circular surface where the block will leave contact with the surface.
The total mechanical energy at the bottom (initial state) is equal to the total mechanical energy at the height h (final state).
12mv20=mgh+12mv2
Here, v is the velocity of the block at height h.
Substitute v0=√4gR into the equation:
12m(4gR)=mgh+12mv2
Simplifying gives:
2mgR=mgh+12mv2
Rearranging the equation to isolate v2:
12mv2=2mgR−mgh
v2=4gR−2gh
For the block to leave the surface, the normal force N must be zero. The forces acting on the block in the vertical direction when it is at height h are:
mgcos(θ)=mv2R
Where θ is the angle from the vertical. Since N=0:
mgcos(θ)=mv2R
Substitute v2 from the previous step:
mgcos(θ)=m(4gR−2gh)R
Simplifying gives:
gcos(θ)=4gR−2ghR
Cancel g (assuming g≠0):
cos(θ)=4R−2hR
Rearranging gives:
cos(θ)=4−2hR
From circular motion, we know:
h=R(1−cos(θ))
Substituting for cos(θ):
h=R(1−(4−2hR))
Simplifying gives:
h=R(−3+2hR)
h=−3R+2h
h−2h=−3R
−h=−3R⟹h=3R
The maximum height from the bottom of the circular surface where the block leaves contact is:
h=2R3
The maximum height from the bottom of the circular surface where the block will leave contact is:
h=5R3
Similar Questions
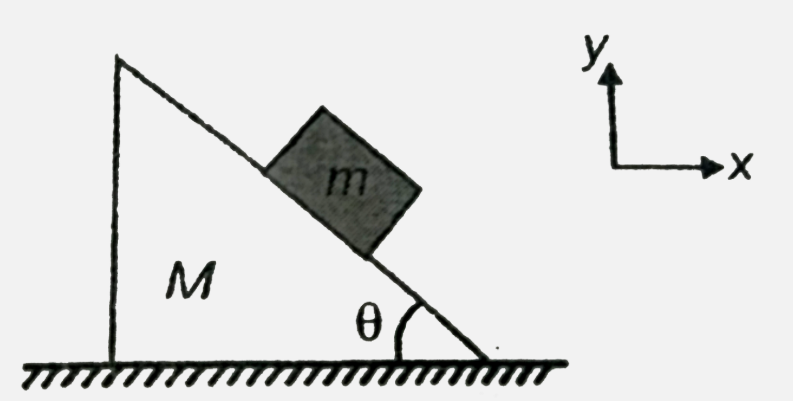
A block of mass m is placed on a smooth wedge of mass M, as shown in the figure . Just after placiing block m over wedge M.
View SolutionA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure Choose the wrong option.

View SolutionA small block of mass m has speed√gR2 at the top most point of a fixed hemisphere of radius R as shown in figure. The angle θ, when block loses the contact with the hemisphere is
_PHY_E05_149_Q01.png)
View SolutionA small block oscillates back and forth on as smooth concave surface of radius R in figure. Find the time period of small oscillation.

View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

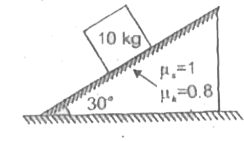
View SolutionA block of 10 kg mass is placed on a rough inclined surface as shown in figure. The acceleration of the block will be
View SolutionA block of mass m slides down along the surface of the bowl from the rim to the bottom as shown in fig. The velocity of the block at the bottom will be-

View SolutionA small block of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. If h be the height of wedge and θ is the inclination, then the distance moved by the wedge as the block reaches the foot of the wedge is
View SolutionA block of mass 10kg is placed on a horizontal surface as shown in the figure and a force F=100N is applied on the block as shown, in the figure. The block is at rest with respect to ground. If the contact force between block and ground is 25n (in Newton) then value of n is : (Takeg=10m/s2)

View SolutionA block of mass m is placed on a triangular block of mass M(M=2m) , as shown. All surfaces are smooth. Calculate the velocity of triangular block when the smaller block reaches at bottom.

View Solution
